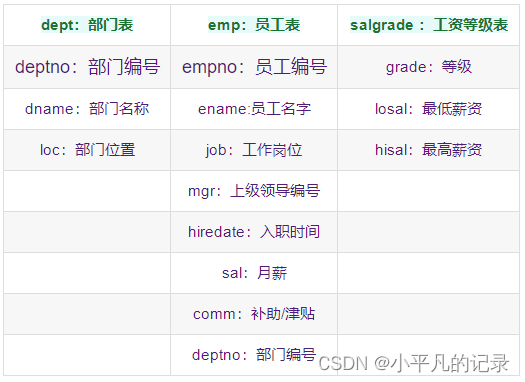
定义
线性模型是在实践中广泛使用的一类模型,几十年来被广泛研究,它可以追溯到一百多年前。线性模型利用输入特征的线性函数
用于回归的线性模型

import mglearn
import matplotlib.pyplot as plt
mglearn.plots.plot_linear_regression_wave()
plt.show()
得到如下图片
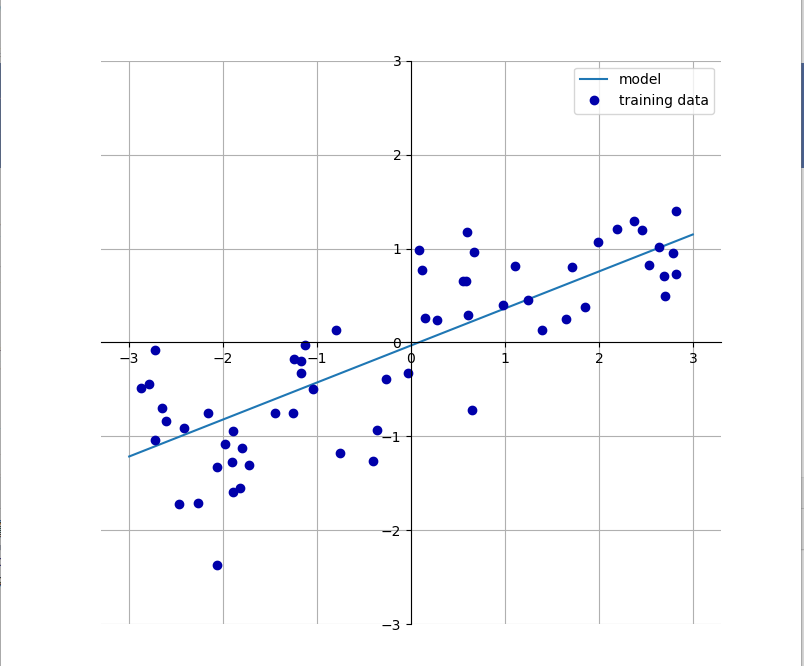
我们在图中添加了坐标网络,便于理解直线的含义。从w[0]可以看出,斜率应该在0.4左右,在图像中也可以直观地确认这一点
截距是指预测直线与y轴的交点;比0略小,也可以在图像中确认,用于回归的线性模型可以表示为这样的回归模型:对单一特征的预测结果是一条直线
两个特征时是一个平面,或者在更高维度时是一个超平面, 有许多不同的线性回归模型。这些模型之间的区别在于如何从训练数据中学习参数w和b,以及如何控制模型模型复杂度。下面介绍最常见的线性回归模型
线性回归(最小二乘法)
线性回归,或者普通最小二乘法,是回归问题最简单也是最经典的线性方法。线性回归寻找参数w和b,使得对训练集的预测值与真实的回归目标值y之间的均方误差最小
均方误差是预测值与真实值之差的平方和除以样本数
线性回归没有参数,这是一个优点,但也因此无法控制模型的复杂度。
接下来我们用代码实现
from sklearn.linear_model import LinearRegression
from mglearn import datasets
#
X, y = mglearn.datasets.make_wave(n_samples=60)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
# 实例化模型
lr = LinearRegression().fit(X_train, y_train)
# 斜率参数(w,也叫作权重或系数)被保存在coef_属性中,而偏移或截距(b)被保存在intercept_属性中
print("lr.coef_:{}".format(lr.coef_))
print("lr.intercept_:{}".format(lr.intercept_))
# 你可能注意到了coef_和intercept_结尾处奇怪的下划线。scikit-learn总是将从训练数据中得到的值保存在以下划线结尾的属性中
# 这是为了将其与用户设置的参数区分开
# intercept_属性是一个浮点数,而coef_属性是一个Numpy数组,每个元素对应一个输入特征。
# 由于wave数据集只有一个输入特征,所以lr.coef_中只有一个元素
# 我们来看一下训练集和测试集的性能:
print("Training set score:{:.2f}".format(lr.score(X_train, y_train)))
print("Test set score:{:.2f}".format(lr.score(X_test, y_test)))
# r^2约为0.66,这个结果不是很好,但我们可以看到,训练集和测试集上的分数非常接近
# 这说明可能存在欠拟合,而不是过拟合
# 对于这个一维数据集来说,过拟合的风险很小
# 因为模型非常简单(或受限)
# 然而,对于更高维的数据集(即有大量特征的数据集)
# 线性模型将变得更加强大,过拟合的可能性也会变大
# 我们来看一下LinearRegression在更复杂的数据集上的表现
# 比如波士顿房价数据集
# 记住,这个数据集有506个样本和105个导出特征
# 首先,加载数据集并将其分为训练集和测试集
# 然后像前面一样构建线性回归模型
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
# 比较一下训练集合测试集的分数就可以发现,我们在训练集的预测非常准确
# 但测试集上的R^2要低很多
print("Training set score:{:.2f}".format(lr.score(X_train, y_train)))
print("Test set score:{:.2f}".format(lr.score(X_test, y_test)))
# 训练集和测试集之间的性能差异是过拟合的明显标志
因此我们应该试图找到一个可以控制复杂度的模型,标准线性回归罪常用的替代方法之一就是岭回归。
岭回归
岭回归是一种用于回归的线性模型,因此他的预测公式与普通的最小二乘法相同
但在岭回归中,对系数(w)的选择不仅要在训练数据上得到好的测试结果,而且还要拟合附加约束
我们还希望系数尽量小
换句话说,w的所有元素都接近于0
直观上来看,这意味着每个特征对输出的影响尽可能小(即斜率很小),同时扔给出很好的预测结果
这种约束是所谓正则化的一个例子
正则化是指对模型显式约束,以避免过拟合,岭回归用到的这种被称为L2正则化
岭回归在linear_model.Ridge中实现,来看一下他对扩展的房价数据集的效果如何
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("Traingning set score:{:.2f}".format(ridge.score(X_train, y_train)))
print("Testing set score:{:.2f}".format(ridge.score(X_test, y_test)))
# 可以看出,Ridge在训练集上的分数要低于LinearRegression,但在测试集上的分数更高
# 这和我们的预期一致。线性回归对于数据存在过拟合。ridge是一种约束性更强的模型
# 所以更不容易过拟合
# 复杂度更小的模型意味着在训练集上的性能更差,但泛化性能更好
# 由于我们只对泛化性能感兴趣,所以应该选择Ridge模型而不是LinearRegression模型
# ridge模型在模型的简单些(系数都接近于0)与训练集性能之间做出权衡
# 简单性和训练集性能二者对于模型的重要程度可以由用户通过设置alpha参数来指定
# 在前面的例子中,我们使用到时默认参数alpha=1.0,但没有理由认为这会给出最佳权衡
# alpha的最佳设定值取决于用到的具体数据集
# 增大alpha会使得系数更加趋近于0,从而降低训练集性能,但可能会提高泛化性能
# 例如
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("Training set score:{:.2f}".format(ridge10.score(X_train, y_train)))
print("Test set score:{:.2f}".format(ridge10.score(X_test, y_test)))
# 减小alpha可以让系数受到的限制更小,对于非常小的alpha值,系数几乎没受到任何限制
# 我们得到一个与Linear_Regression类似的模型
ridge01 = Ridge(alpha=0.1).fit(X_train, y_train)
print("Training set score:{:.2f}".format(ridge01.score(X_train, y_train)))
print("Test set score:{:.2f}".format(ridge01.score(X_test, y_test)))
# 这里alpha=0.1似乎效果不错。我们可以尝试进一步减小alpha以提高泛化性能
# 现在,注意参数alpha与图2-1中的模型复杂度的对应关系
# 我们还可以查看alpha取不同值时模型的coef_属性,从而更加定性的理解alpha参数是如何改变模型的
# 更大的alpha表示约束更强的模型
# 所以我们预计大alpha对应的coef_元素比小alpha对应的coef_元素要小
接下来我们通过绘制图像来查看正则化系数alpha取不同值对各特征权重(w)的影响
plt.plot(ridge.coef_, 's', label='Ridge alpha=1')
plt.plot(ridge10.coef_, '^', label='Ridge alpha=10')
plt.plot(ridge10.coef_, '^', label='Ridge alpha=10')
plt.plot(lr.coef_, 'o', label='Ridge alpha=0.1')
plt.xlabel("Coefficent index")
plt.ylabel("Coefficent magnitude")
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()
plt.show()
得到如下图片
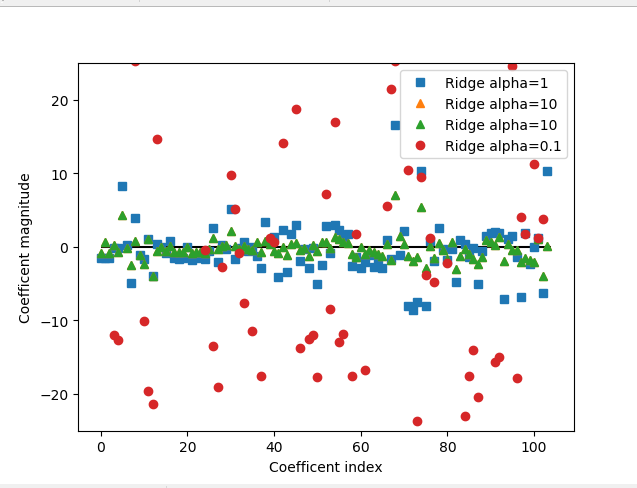
这次绘制图片主要针对延展波士顿房价的数据集,这个数据集每条数据有105个特征,图中x轴对于coef_(斜率或权重)的元素;x=0对应第一个特征的系数,x=1对应第二个特征的系数,以此类推,一直到x=105。y轴表示该系数的具体数值。这里需要记住的是,对于alpha=10,系数大多在-3到3之间。对于alpha=1的Ridge模型,系数要稍大一些。对于alpha=0.1,点的范围更大。对于没有做正则化的线性回归(即alpha=0)
还有一种方法可以用来理解正则化的影响,就是固定alpha值,但改变训练数据量,我们对波士顿房价数据做二次抽样,并在数据量逐渐增加的子数据集上分别对LinearRegression和Ridge(alpha=1)两个模型进行评估(将模型性能作为数据集大小的函数进行绘图,这样的图像叫作学习曲线,)
mglearn.plots.plot_ridge_n_samples()
plt.show()
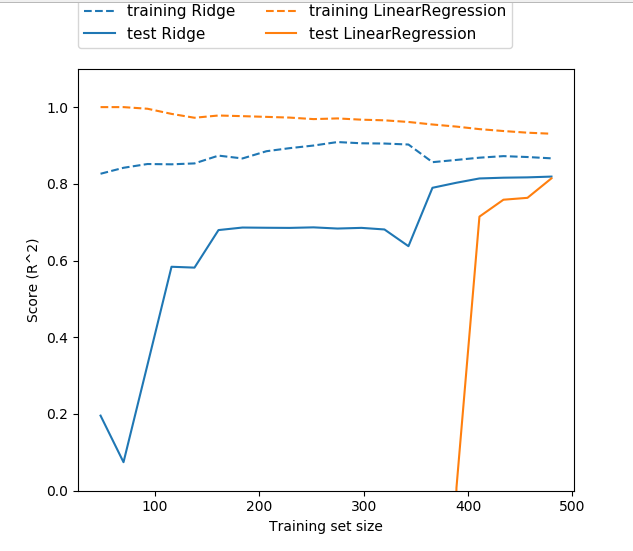
正如所设计的那样,无论是岭回归还是线性回归,所有数据集大小对应的训练分数都要高于测试分数。由于岭回归是正则化的,因此他的训练分数要整体低于线性回归的训练分数。但岭回归的测试分数要更高,特别是对于较小的子数据集。如果少于400个数据点,线性回归将学不到任何内容。随着模型可用的数据越来越多,两个模型的性能都在提升,最终线性回归的性能追上了岭回归。这里要记住的是,如果有足够多的训练数据,正则化变得不那么重要,并且岭回归和线性回归将具有相同的性能(在这个例子中,二者相同恰好发生在整个数据集的情况下,这只是一个巧合)。上图还有一个有趣之处,就是线性回归的训练性能在下降。如果添加更多数据,模型将更加难以过拟合或记住所有的数据。
lasso
除了ridge,还有一种正则化的线性回归是lasso。与岭回归相同,使用lasso也是约束系数使其接近于0,但用到的方法不同,叫做L1正则化。L1正则化的结果是,使用lasso时某些系数刚好为0。这说明模型更容易解释,也可以呈现模型最重要的特征。
我们将lasso应用在扩展的波士顿房价数据集上
import numpy as np
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train,y_train)
print("Training set score :{:.2f}".format(lasso.score(X_train,y_train)))
print("Test set score :{:.2f}".format(lasso.score(X_train,y_train)))
print("Number of features used:{}".format(np.sum(lasso.coef_!=0)))
# 输出的结果为
# Training set score :0.29
# Test set score :0.29
# Number of features used:4
# 如你所见,Lasso在训练集与测试集上的表现都很差。这表示存在欠拟合
# 我们发现模型只用到了105个特征中的4个。
与Ridge类似,Lasso也有一个正则化参数alpha,可以控制系数趋向于0的强度,在上一个例子中,我们用的是默认值alpha=1.0,为了降低欠拟合,我们尝试减小alpha, 这么做的同时,我们还需要增加max_iter的值(运行迭代的最大次数)。
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("Training set score:{:.2f}".format(lasso001.score(X_train, y_train)))
print("Testing set score:{:.2f}".format(lasso001.score(X_test, y_test)))
print("Number of features used:{}".format(np.sum(lasso001.coef_ != 0)))
# 输出结果为:
# Training set score:0.90
# Testing set score:0.77
# Number of features used:33
# alpha值变小,我们可以拟合一个更复杂的模型,在训练集上和测试集上的表现也更好
# 模型性能比使用Ridge时略好一些,而且我们只用到了105个特征中的33个。这样模型可能更容易理解
但如果把alpha设的太小,那么就会消除正则化的效果,并出现过拟合,得到与linearRegression类似的结果
lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print("Training set score:{:.2f}".format(lasso00001.score(X_train, y_train)))
print("Testing set score:{:.2f}".format(lasso00001.score(X_test, y_test)))
print("Number of features used:{}".format(np.sum(lasso00001.coef_ != 0)))
# 输出结果为Training set score:0.95
# Testing set score:0.64
# Number of features used:94
再次像图2-12那样对不同模型的系数进行作图
plt.plot(lasso.coef_, 's', label='Lasso alpha=1')
plt.plot(lasso001.coef_, '^', label='Lasso alpha=0.01')
plt.plot(lasso00001.coef_, 'v', label='Lasso alpha=0.0001')
plt.plot(ridge01.coef_, 'o', label='Ridge alpha=0.1')
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.show()
得到如下图片
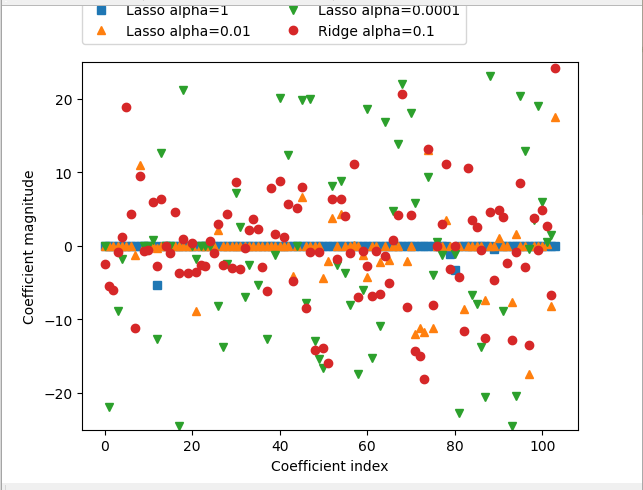
在alpha=1时,我们发现不仅大部分系数都是0(我们已经知道这一点),而且其他系数也很小。将alpha减小至0.1,我们得到图中向上的三角形,大部分特征等于0.alpha=0.0001时,我们得到正则化很弱的模型,大部分系数都不为0,并且还很大。为了便于比较,图中用圆形表示ridge的最佳结果。alpha=0.1的ridge模型的预测性能与alpha=0.1的Lasso模型类似,但Ridge模型的所有系数都不为0。
在实践中,在两个模型中一般首选岭回归,但如果特征很多,你认为只有其中几个是重要的,那么选择Lasso可能更好。同样,如果你想要一个容易解释的模型,Lasso可以给出更容易理解的模型,因为它只选择了一部分输入特征。scikit-learn还提供了ElasticNet类,结合了Lasso和Ridge的惩罚项。在实践中,这种结合的效果很好,不过代价是要调节两个参数;一个用于L1正则化,一个用于L2正则化。