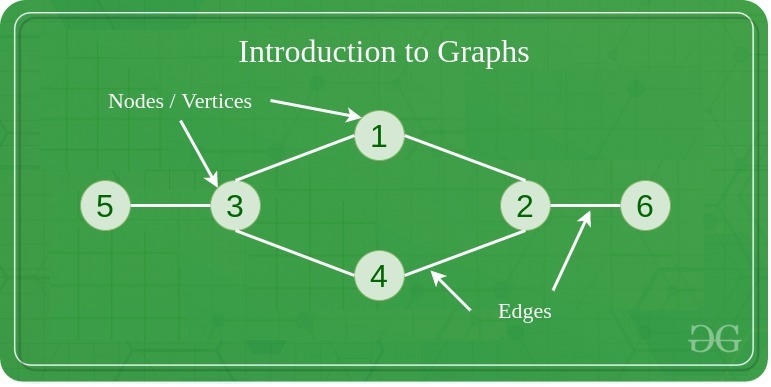
前置知识
回溯算法模板框架如下:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
注意这里的for,回溯问题可以看成树问题,但是N叉树,
而不一定是二叉树。
看一下589.N叉树的前序遍历就很好理解了
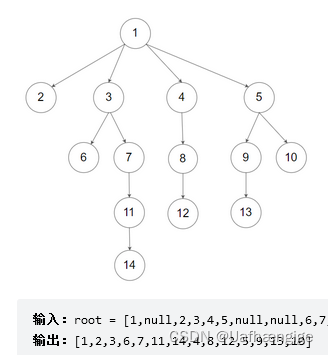
class Solution {
public:
vector<int> res;
vector<int> preorder(Node* root) {
traversal(root);
return res;
}
void traversal(Node* root){
if(root == nullptr) return ;
res.push_back(root->val);
for(int i = 0; i < root->children.size(); ++i){
traversal(root->children[i]);
}
}
};
对于组合问题,什么时候需要startIndex呢?
我举过例子,如果是一个集合来求组合的话,就需要startIndex, 例如:77.组合
(opens new window),216.组合总和III
(opens new window)。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:17.电话号码的字母组合
第77题. 组合
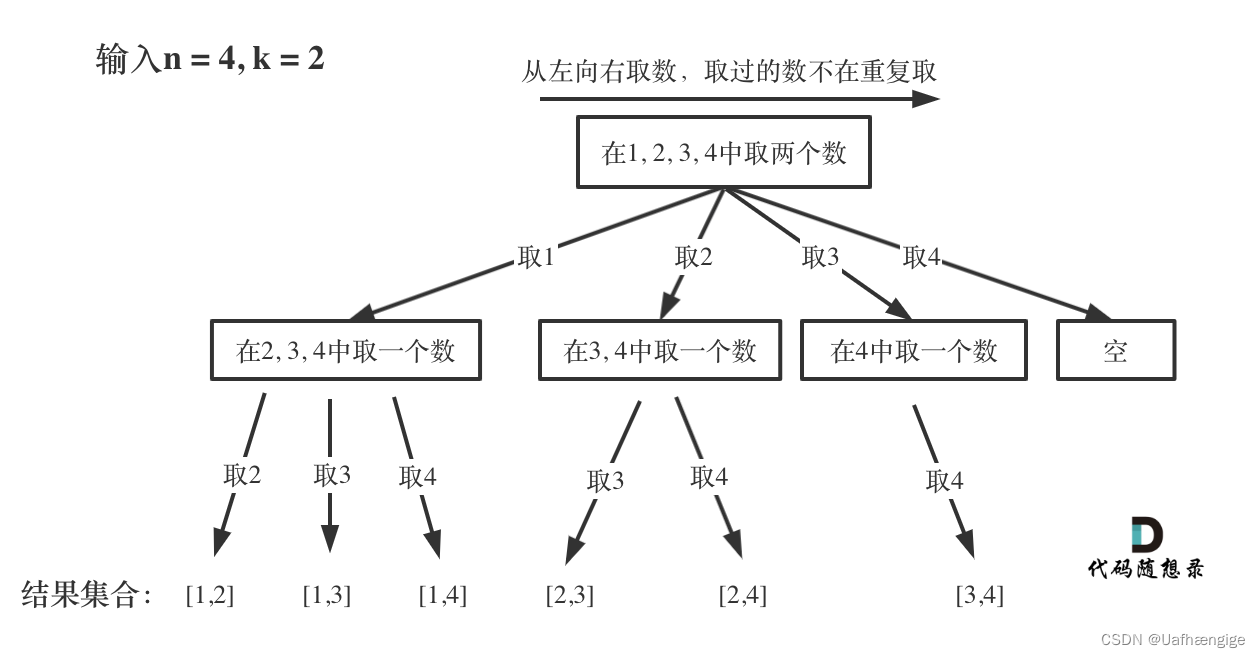
不难 按照模板的思路来,考虑成N叉树的层序遍历就行。
当k = 2, n = 4时
class Solution {
public:
vector<vector<int>> res;
vector<int> vec;
vector<vector<int>> combine(int n, int k) {
backtracking(n,k,vec,1);
return res;
}
void backtracking(int n,int k,vector<int>& vec,int start){
if(vec.size() == k) {
res.push_back(vec);
return;
}
for(int i = start; i <= n; ++i){
vec.push_back(i);
backtracking(n,k,vec,i+1);
vec.pop_back();
}
}
};
接下来看一下优化过程如下:
1、已经选择的元素个数:path.size();
2、还需要的元素个数为: k - path.size();
3、在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
从2开始搜索都是合理的,可以是组合[2, 3, 4]。
这里大家想不懂的话,建议也举一个例子,就知道是不是要+1了。
所以优化之后的for循环是:
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
216.组合总和III
不难,但是递归的时候要注意是 i+1,而不是start+1;
class Solution {
public:
vector<vector<int>> res;
vector<int> vec;
vector<vector<int>> combinationSum3(int k, int n) {
backtracking(k,n,1);
return res;
}
void backtracking(int k, int n, int start){
int sum = 0;
for(int a : vec) sum += a;
if(vec.size() == k && sum == n) {
res.push_back(vec);
return;
}
for(int i = start; i <= 9 && vec.size() < k && i + sum <= n ; ++i){
vec.push_back(i);
backtracking(k,n,i+1);
vec.pop_back();
}
}
};
17.电话号码的字母组合
电话号码的数字和字符串对应可以直接用数组来解决。另外index一定是整数,注意数据类型之间的转换
本题的广度就是 数字对应字符串的长度。深度是digits的长度
class Solution {
public:
string phone[10] = {
"0",
"0",
"abc",
"def",
"ghi",
"jkl",
"mno",
"pqrs",
"tuv",
"wxyz"
};
vector<string> res;
vector<char> vec;
vector<string> letterCombinations(string digits) {
if(digits.size() == 0) return res;
backtracking(digits,0);
return res;
}
void backtracking(string digits,int start){
if(vec.size() == digits.size()){
string str = "";
for(char c : vec) str += c;
res.push_back(str);
return;
}
for(int i = start; i < digits.size(); ++i){ //这一层for其实没有必要,本题的广度就是 数字对应字符串的长度。深度是digits的长度
//digits[i] 是char类型 但是index一定是int
int index = digits[i] - '0';
for(int j = 0; j < phone[index].size(); ++j){
vec.push_back(phone[index][j]);
backtracking(digits,i+1);
vec.pop_back();
}
}
}
};
39. 组合总和
注意去重,要重新再写一遍
class Solution {
public:
vector<vector<int>> res;
vector<int> vec;
int sum = 0;
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
backtracking(candidates,target,0);
return res;
}
void backtracking(vector<int> candidates,int target,int start){
if(sum > target) return;
if(sum == target) res.push_back(vec);
for(int i = start; i < candidates.size(); ++i){
vec.push_back(candidates[i]);
sum += candidates[i];
if(sum > target){
sum -= candidates[i];
vec.pop_back();
break;
}
backtracking(candidates,target,i);
sum -= candidates[i];
vec.pop_back();
}
}
};
40.组合总和II
去重的时候也可以用used数组
class Solution {
public:
vector<vector<int>> res;
vector<int> vec;
int sum = 0;
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
backtracking(candidates,target,0);
return res;
}
void backtracking(vector<int>& candidates,int target,int start){
if(sum > target) return;
if(sum == target) res.push_back(vec);
for(int i = start; i < candidates.size() && sum + candidates[i] <= target; ++i){
if(i > start && candidates[i-1] == candidates[i]) continue;
vec.push_back(candidates[i]);
sum += candidates[i];
backtracking(candidates,target,i+1);
sum -= candidates[i];
vec.pop_back();
}
}
};
131.分割回文串
自己写出来的AC了,但是可以优化。
优化点:
1、使用startIndex来区分切割区间
2、直接判断当前字符串是否是回文,再看下一步是否递归
class Solution {
public:
vector<vector<string>> res;
vector<string> vec;
vector<vector<string>> partition(string s) {
backtracking(s);
return res;
}
void backtracking(string s){
if("" == s){
bool bres = hui(vec);
if(bres == true) res.push_back(vec);
else return;
}
for(int i = 0; i < s.size(); ++i){
vec.push_back(string(s.begin(),s.begin()+i+1));
backtracking(string(s.begin()+i+1,s.end()));
vec.pop_back();
}
}
bool hui(vector<string>& vec){
for(string s : vec){
int left = 0;
int right = s.size()-1;
for(int i = left,j = right; i < j; ++i,--j){
if(s[i] != s[j]) return false;
}
}
return true;
}
};
优化代码:
class Solution {
public:
vector<vector<string>> res;
vector<string> vec;
vector<vector<string>> partition(string s) {
backtracking(s,0);
return res;
}
void backtracking(string s,int start){
if(start >= s.size()){
res.push_back(vec);
return;
}
for(int i = start; i < s.size(); ++i){
string str(s.begin()+start,s.begin()+i+1);
bool bres = hui(str);
if(bres == false) continue;
//直接在这一步判断,也起到一个剪枝的效果
vec.push_back(str);
backtracking(s,i+1);
vec.pop_back();
}
}
bool hui(string s){
int left = 0;
int right = s.size()-1;
for(int i = left,j = right; i < j; ++i,--j){
if(s[i] != s[j]) return false;
}
return true;
}
};