1、LDA的手动处理

LDA（线性判别分析）是特征变换算法，也是有监督分类器。

和PCA一样，LDA的目标是提取一个新的坐标系，将原始的数据集投影到一个低维的空间中。
和PCA的主要区别是，LDA不会专注数据的方差，而是优化低维空间，以获得最佳的类别可分性。

LDA极为有用的原因在于，基于类别可分性的分类有助于避免机器学习流水线的过拟合。也会降低计算成本。

LDA不会计算整体数据的协方差矩阵的特征值，而是计算类内(within-class)和类间(between-class)散布矩阵的特征值和特征向量。
LDA分为5个步骤：
1、计算每个类别的均值向量
2、计算类内和类间的散布矩阵
3、计算S(W)-1 * S(B) 的特征值和特征向量
4、降序排列特征值，保留前K个特征向量
5、使用前几个特征向量，将数据投影到新空间

（1）计算每个类别的均值向量

import matplotlib as mpl
# 解决中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

# 从sklearn中导入鸢尾花数据集
from sklearn.datasets import load_iris
import numpy as np
# 导入画图模块
import matplotlib.pyplot as plt
%matplotlib inline

# (1)、加载数据集
iris = load_iris()

# (2)、将数据矩阵和相应变量存储到iris_x和iris_y中
iris_X, iris_y = iris.data, iris.target

label_dict = {i : k for i,k in enumerate(iris.target_names)}
print(label_dict)
# {0: 'setosa', 1: 'versicolor', 2: 'virginica'}

'''
第一步、计算每个类别的均值向量
'''


# 每个类别的均值向量
mean_vect = []

for cl in [0, 1, 2]:
    # 过滤出每一种鸢尾花，计算其均值向量
    class_mean_vect = np.mean(iris_X[iris_y == cl], axis=0)
    print(label_dict[cl],'均值向量为: ', class_mean_vect)
    mean_vect.append(class_mean_vect)
mean_vect

（2）计算类内和类间的散布矩阵

'''
第二步、计算类内和类间的散布矩阵
'''

# (1) 计算类内的散布矩阵S_W
S_W = np.zeros((4, 4))

list(zip([0, 1 , 2], mean_vect))

# 对于每种鸢尾花
for cl, mv in zip([0, 1 , 2], mean_vect):
    # 从0开始，每个类别的散布矩阵
    class_sc_mat = np.zeros((4, 4))
    # 对于每个样本
    for row in iris_X[iris_y == cl]:
        row = row.reshape(4, 1)
        mv = mv.reshape(4, 1)
        # 4 * 4矩阵
        class_sc_mat = class_sc_mat + (row - mv).dot((row - mv).T)
    # 散布矩阵的和
    S_W += class_sc_mat

S_W

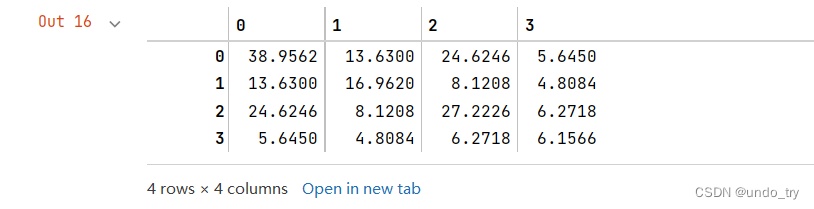
# (2) 计算类间的散布矩阵S_B

# 整个数据集的均值
total_mean = np.mean(iris_X, axis=0).reshape(4, 1)
S_B = np.zeros((4, 4))
for i,mean_vec in enumerate(mean_vect):
    # 每一种鸢尾花的数量
    n = iris_X[iris_y == i, :].shape[0]
    # 每种花的列向量
    mean_vec = mean_vec.reshape(4, 1)

    S_B = S_B + n * (mean_vec-total_mean).dot((mean_vec-total_mean).T)

S_B

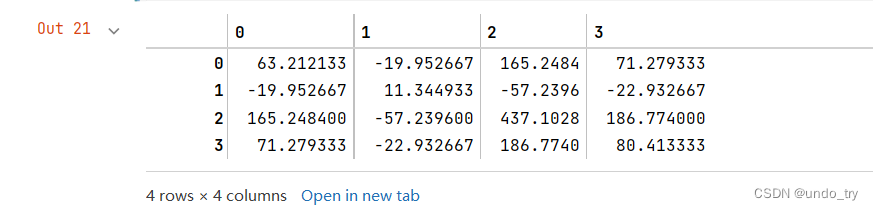
（3）计算S(W)-1 * S(B) 的特征值和特征向量

'''
第三步、计算S(W)-1 * S(B) 的特征值和特征向量
'''
# 利用eig进行矩阵分解(inv求逆)
eig_values, eig_vecs = np.linalg.eig(
    np.dot(
        np.linalg.inv(S_W), S_B
    )
)

eig_values = eig_values.real
eig_vecs = eig_vecs.real


# 按照降序打印特征向量和相应的特征值
for i in range(len(eig_values)):
    eigvec_cov = eig_vecs[:, i]
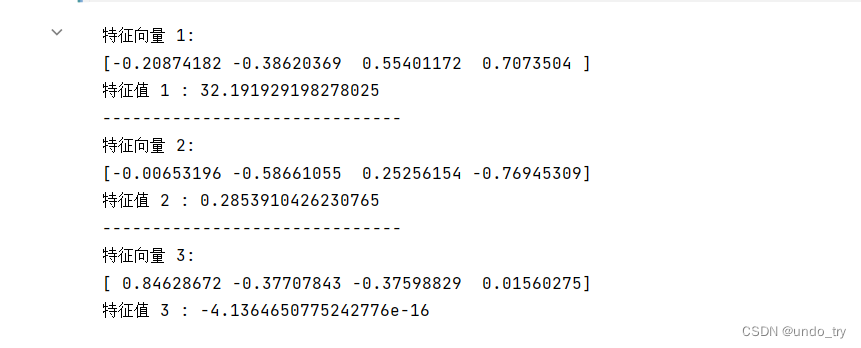
    print('特征向量 {}: \n{}'.format(i + 1, eigvec_cov))
    print('特征值 {} : {}'.format(i + 1,eig_values[i]))
    print(30 * '-')

# 注意，第3个和第4个特征值几乎为0，这是因为LDA在类间划分决策边界，鸢尾花数据集只有三个类别，我们可能只需要2个决策边界
# 通常来说，LDA拟合n个类别的数据集，最多只需要n-1次切割

（4）降序排列特征值，保留前K个特征向量

'''
第四步、降序排列特征值，保留前K个特征向量
'''

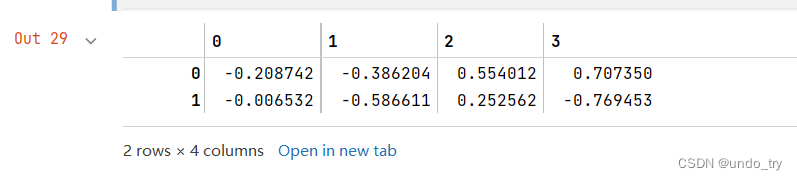
# 保留最好的两个线性判别式子
line_dis = eig_vecs.T[:2]

line_dis

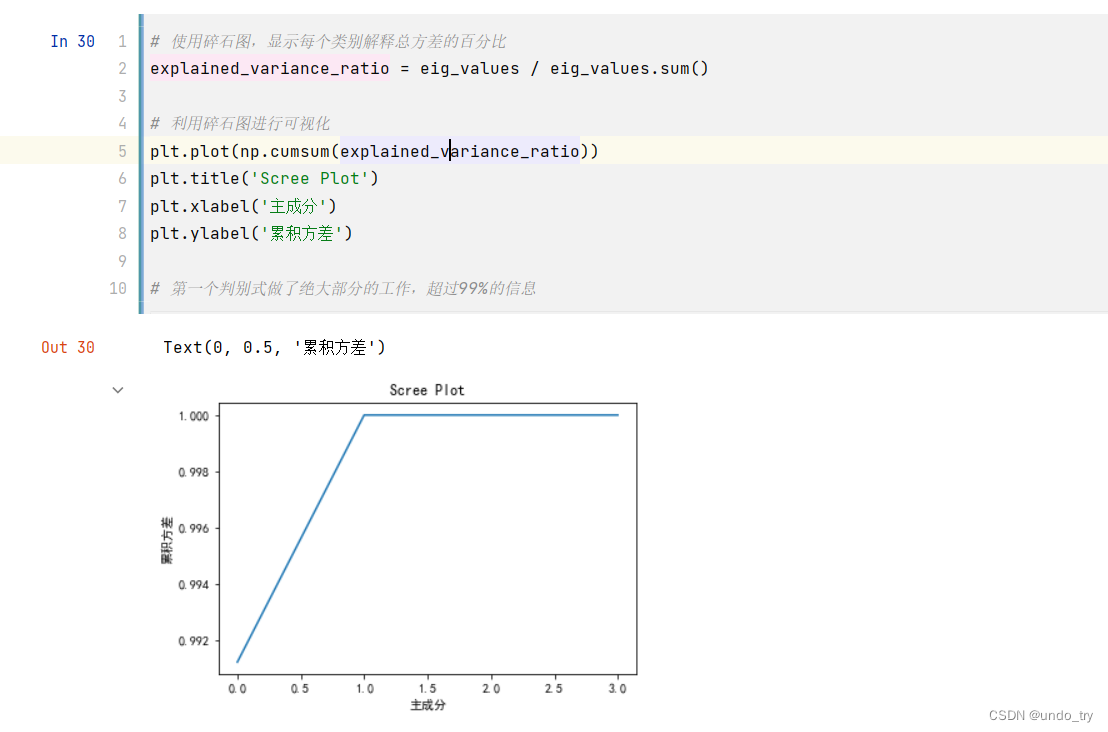
（5）使用前几个特征向量，将数据投影到新空间

'''
第五步、使用前几个特征向量，将数据投影到新空间
'''
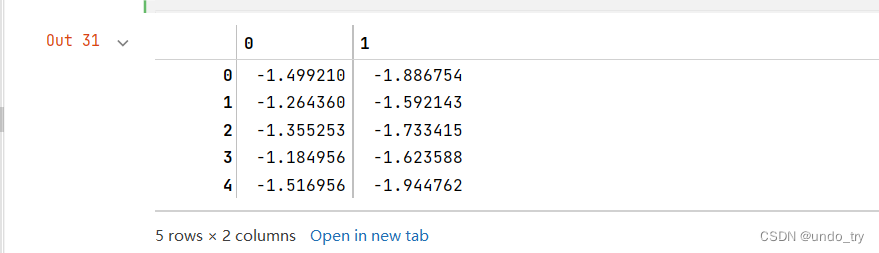
lda_projection = np.dot(iris_X, line_dis.T)
lda_projection[:5, :]

def plot(X, y, title, x_label, y_label):
    ax = plt.subplot(111)
    for label,market,color in zip(range(3),('^', 's' , 'o'), ('blue', 'red', 'green')):
        plt.scatter(
            x=X[:, 0].real[y == label],
            y = X[:, 1].real[y == label],
            color=color,
            alpha=0.5,
            label=label_dict[label]
                    )

    plt.xlabel(x_label)
    plt.ylabel(y_label)

    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title(title)


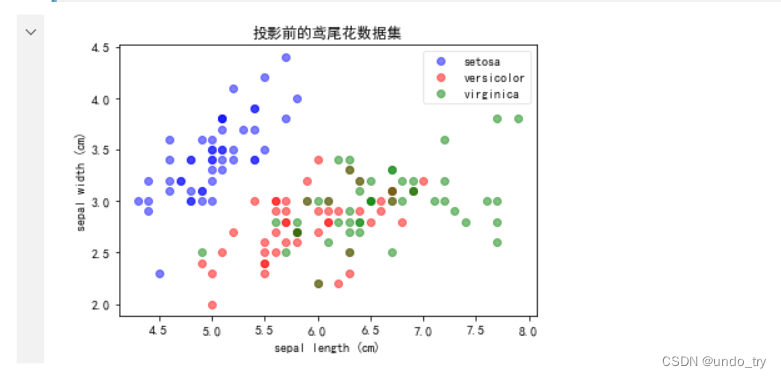
# 投影前的鸢尾花数据集
plot(iris_X, iris_y, '投影前的鸢尾花数据集', 'sepal length (cm)', 'sepal width (cm)')

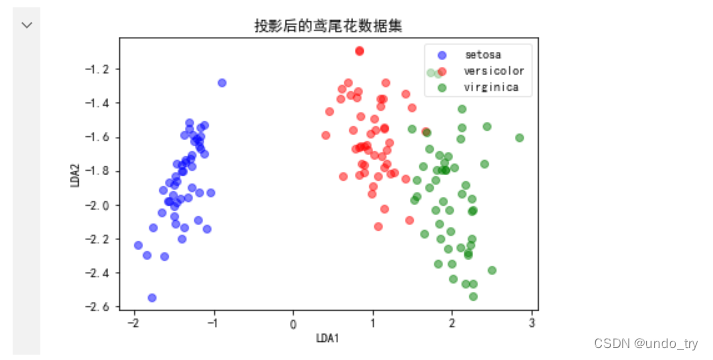
# 投影后的鸢尾花数据集
plot(lda_projection, iris_y, '投影后的鸢尾花数据集', 'LDA1', 'LDA2')

# 可以看到数据几乎完全突出出来了，因为LDA会绘制决策边界，提供特征向量，从而帮助机器学习模型尽可能的分裂各种花。

2、scikit-learn中的LDA

import matplotlib as mpl
# 解决中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

# 从sklearn中导入鸢尾花数据集
from sklearn.datasets import load_iris
import numpy as np
# 导入画图模块
import matplotlib.pyplot as plt
%matplotlib inline


# (1)、加载数据集
iris = load_iris()

# (2)、将数据矩阵和相应变量存储到iris_x和iris_y中
iris_X, iris_y = iris.data, iris.target
label_dict = {i : k for i,k in enumerate(iris.target_names)}

# 导入LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# LDA其实是伪装成特征转换算法的分类器
# 和PCA无监督计算不同，LDA会尝试用响应变量，查找最佳的坐标系，尽可能优化类别的可分性
# LDA只有在有响应变量存在的时候才能用
lda = LinearDiscriminantAnalysis(n_components=2)

# 拟合并转换鸢尾花数据集
X_lda_iris = lda.fit_transform(iris_X, iris_y)


def plot(X, y, title, x_label, y_label):
    ax = plt.subplot(111)
    for label,market,color in zip(range(3),('^', 's' , 'o'), ('blue', 'red', 'green')):
        plt.scatter(
            x=X[:, 0].real[y == label],
            y = X[:, 1].real[y == label],
            color=color,
            alpha=0.5,
            label=label_dict[label]
                    )

    plt.xlabel(x_label)
    plt.ylabel(y_label)

    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.5)
    plt.title(title)


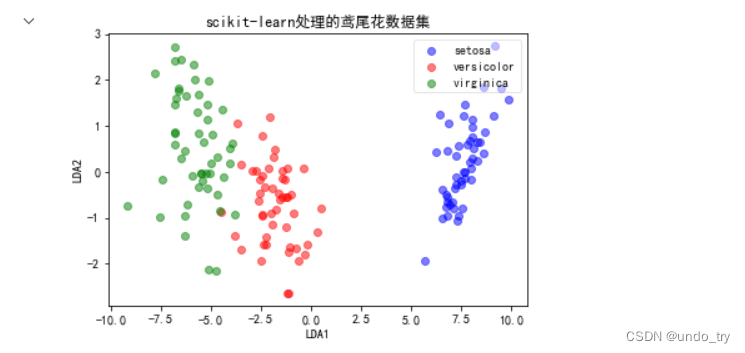
# 投影前的鸢尾花数据集
plot(X_lda_iris, iris_y, 'scikit-learn处理的鸢尾花数据集', 'LDA1', 'LDA2')

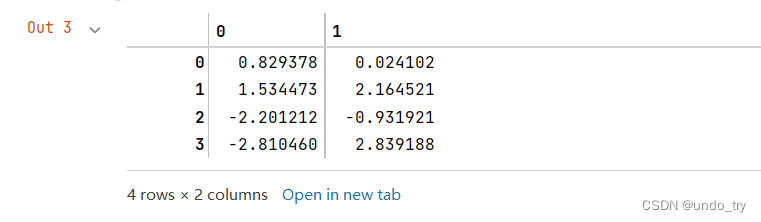
# lda的scalings和pca的compents_基本一样，但是转置了_
lda.scalings_

# 解释方差lda.explained_variance_ratio_和手动计算完全相同，不过判别式好像之前手动计算的特征向量完全不同，这是因为scikit-learn进行了标量缩放
# 和PCA一样，投影是原始列的一个线性组合
# LDA和PCA一样，会去除特征的相关性
# PCA和LDA的主要区别在于：PCA是无监督方法，捕获整个数据集的方差；而LDA是有监督的方法，通过响应变量来捕获类别的可分性。