引言

笔者一直觉得在计算机这一学科的学习中，离散数学是极为重要的知识基础。离散化的思想体现在计算机学科的方方面面。举例来说，“像素”这一概念是我们日常生活中耳熟能详的，将一个图片拆分成一个个极微小的像素，就是利用了离散化的思想。为了帮助大家打好离散数学的思维基础，笔者新开一个专栏，对《离散数学导学》这本书做一个精炼，使其更易理解。这篇文章是这个专栏的第三部分，主要介绍6-7章。
1-3章传送门
4-5章传送门

正文

第六章 类型集合论

类型的需要

一个含有不同类型的集合是没有意义的。我们规定，一个集合中的元素一定要是同一类型的。
空集也含有类型，一个自然数类型的空集和一个集合类型的空集是不一样的。

集合描述

一个集合描述以如下形式出现：

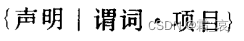
1. 声明：声明元素属于哪一类型（实际不一定是这个集合中的元素）
2. 谓词：起到过滤器的作用，不满足谓词要求的元素不包含的集合内
3. 项目：集合中元素的输出方式。

我们用一个例子说明一下：

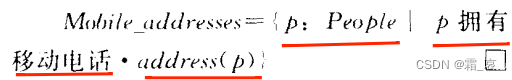
其中，第一条红线是声明p是people类型的，第二条红线要求只有“有移动电话”的p才能保留下来，第三条红线要求集合中实际包含的是每个p元素的address()函数，也就是每个p的地址。

在实际中，谓词和项目都可以省略。

缩写

两个自然数x，y，我们可以用x…y来表示[x,y]。

笛卡尔积（重点）

1. 序偶：x，y分别是两个任意类型的元素，则（x，y）是一个序偶。
2. 笛卡尔积：笛卡尔积是序偶的集合。我们举个例子来理解笛卡尔积：

如果A={1，2}，B={m，n}，则A和B的笛卡尔积，用A×B表示，则为{（1，m），（1，n），（2，m），（2，n）}。

3. 序偶的类型：如果1是N（自然数）类型，a是letter（字母）类型，则（1，a）是N×letter类型。
   注意：（1，a）和（a，1）是不同的类型。

任意集合和空集的笛卡尔积是空集。

4. 注意：我们假设集合A的元素类型是a，集合B的元素类型是b，集合C的元素类型是C，则A×B×C的类型是（（a，b），c），而非直观的（a，b，c）。
5. 成分筛选：成分筛选用.运算符，继续举例子说明：

{p：A×B|p=(a，b)·p.1}，这个集合是{a}，也就是所有元素p的第一个部分。如果p有两个（a，b），（c，d），则前面的集合就是{a，c}。

公理定义

我们可以用公理定义来定义一个集合：

和谓词描述不同，公理定义也可以直接声明集合：

1. 这个公理定义声明了集合中的元素，与上文的谓词描述相似
   
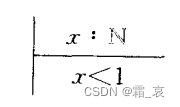
2. 下面的公理定义直接声明集合（P(N)是N的幂集，声明的意思是X是N的一个子集）
   
   

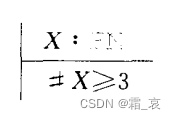
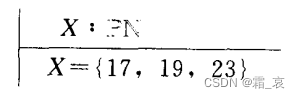
第七章 谓词逻辑

谓词逻辑其实就是命题逻辑的一种简洁的写法

全称量词∀，存在量词∃

这俩没什么说的，大家都知道。

可满足性，有效性，不可满足性

谓词逻辑构成的语句是一个命题，因此也具有真值。

1. 有效性：当一个谓词中的变元取定义域的任意值时，这个命题都为真时，我们称这个谓词（注意是谓词，不是整个命题）时有效的。
   
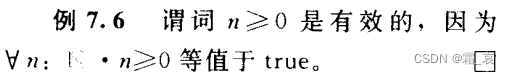
   全称量词表示n取其定义域的任意值。
2. 可满足性：谓词中的变元取定义域的某一个值时，这个命题为真，则称这个谓词是可满足的。
   
   存在量词表示n取其定义域的某一个值。
3. 不可满足性：变元取任意值命题都是假的，谓词就不可满足，不用多说。

自由变元，约束变元

有定义域的变元就是自由变元，否则是约束变元。例如：

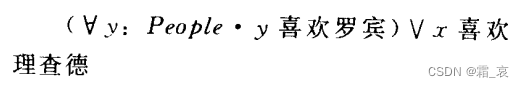
其中y有定义域，是约束变元，x是自由变元。
注意：定义域是有自己的影响范围的，在影响范围之外的该变元依然是自由变元。

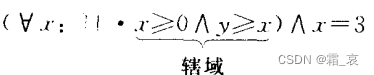
替换

替换符号是[]，我们用例子来说明：

n>0[3/n]的结果是3>0，就是将所有n的地方写成3即可。

只有自由变元能被替换，约束变元收到定义域的限制，如果被替换了，则定义域中少了一个符号，意义完全不同，例如：

∀n：N·n>0[3/n]的结果是∀n：N·n>0，是不变的。如果被替换了，则为∀n：N·3>0，这样在定义域中n这个符号就消失了，这显然是不行的。

依次替换和同时替换

在替换多个变元时，有依次替换和同时替换两种方式。

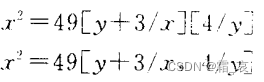
前者是依次替换，后者是同时替换。这两者没什么区别，只是前者分两步替换，后者直接一步替换。

变元俘获

如果用约束变元替换自由变元，那么这个变元也会受到定义域的限制，就发生了变元俘获。
解决方法也很简单，换个字母替换自由变元，或者将约束变元换个字母就可以了。

限制

限制其实就是命题逻辑中的谓词。举个例子就明白了：

红线的部分就是这个命题逻辑的限制。

限制的转化（难点）

限制的转化就是将带有限制的陈述转换成不带有限制的陈述。对于全称量词和存在量词来说，转化的方式是不同的。具体如下：

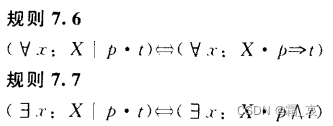
可以看出，全称量词的陈述转化之后用的是蕴含符号，而存在量词的陈述用的是合取符号。其实也不难理解，可以自己举一个全称量词和存在量词的例子，然后你会发现，全称量词都可以用“如果…，就…”这样的句式描述，而存在量词一般用“…的…”比较合适。
例如，下面的陈述：

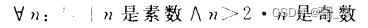
这句话可以说成“如果n是自然数、n是素数且大于2，那么n是奇数。”
再看下面的陈述：

这句话显然说成“存在一个女性的英国首相"比较合适。

唯一存在量词

唯一存在量词是”有且只有“的意思，我们举一个例子说明：

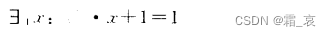
这个描述表示”有且只有一个x，使x+1=1“。

还有一个表示这个x的符号μ：

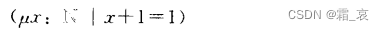
这个描述表示满足这个条件的x的集合，这个集合中只有一个元素。
注意：如果你算出来这个集合中不止一个元素，那么这个符号没有意义。这个符号是专用于唯一存在量词的。

等值推理

我们介绍过命题逻辑的等值推理，作为命题逻辑运算的延伸，谓词逻辑当然有自己的等值推理公式。与谓词逻辑不同的是，这里的等值推理公式距离我们的惯性思维较远，因此需要列出，但依然不需要每个都说明：

1. 下面的公式是自己想不到，但很容易理解的：
   
   
   
   
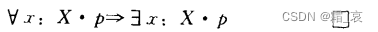
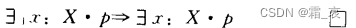
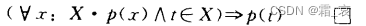
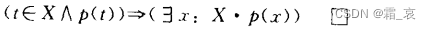
2. 下面的公式是显然性的：
   
3. 下面的四个公式则需要仔细思考一下。注意，这四个公式的前提是x在q中没有出现：
   
   
   
   
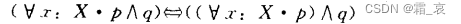
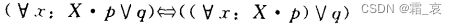
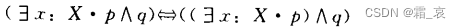
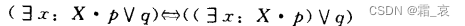
   既然x在q中没有出现，那么x与q没有关系，那么自然可以把q从括号中提出来。

自然演绎

谓词逻辑自然也有自己的自然演绎公式。在说明这些公式之前，提醒一下，在自然演绎中，上面的部分是前提，下面的部分是结论。另外，由于全称量词就是广义交运算，而存在量词是广义并运算，因此可以将带有这两个量词的描述拆成多个交或并运算来理解：


说明一下这个公式，这个公式指任取X集合中的x，经过若干步推导得到p，则结论成立。

这个规则不好理解，笔者的理解是：如果存在x使p为真，且以p为真为假设能推出q，那么q也可以为真；但x在q中不出现，那么q的真假与x没有关系，也就是说q的真假从x的角度来看是无法改变的，关于这一点，举一个例子来理解。看下面的这个描述：

∃x|x∈N·y

很显然这个描述是否为真和x的取值是没有关系的。那么如果存在x能推出这个陈述为真，那么对于所有x，这个陈述也是真的。
回到刚才的说明，q的真值和x的取值也没有关系，因此只要存在一个x推出q是真的，那么对于所有x，q都是真的，结论成立。
对于多个命题来说，这个规则也是成立的：

one-point规则

这个规则如下：

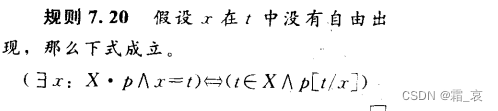
正如这个规则所说，它可以得出t是X的一个元素且t满足p。注意，x在t中没有自由出现的前提很重要，如果用含有x的t来替换x，很显然不能得出什么元素能满足p。

我是霜_哀，在算法之路上努力前行的一位萌新，感谢你的阅读！如果觉得好的话，可以关注一下，我会在将来带来更多更全面的算法讲解！