线性代数 --- Gram-Schmidt, 格拉姆-施密特正交化（上）

在求解最小二乘的问题时，已经介绍了类似于Gram-Schmidt的一些想法。在这里要继续介绍这些想法，那就是如何“改写”矩阵A中的列向量，使得最小二乘解的计算越来越简单，甚至可以直接写出答案。

标准正交基(Orthonormal Bases)

上一篇文章中，我们结束在三个观测点分别在t=(1,3,5)这三个时刻所得到的观测值b1,b2,b3的最小二乘直线拟合b=C+Dt。当时，我们为了让正规方程 $A^{T}A\hat{x}=A^{T}b$ 更好解，通过把t减去他的均值3，得到T=t-3=(-2,0,2)，实现了最小二乘解 $\hat{x}$ 的快速求解(即不是简单的通过套用公式 $\hat{x}=(A^{T}A)^{-1}A^{T}b$ 来计算，而是直接求解正规方程，这样一来，也避免了求 $A^{T}A$ 的逆，这种精度误差较大的运算)。

首先，对于三个数据点(t1=1,b1=1),(t2=3,b2=2),(t3=5,b3=4)而言，因A的两个列向量不是正交的， $A^{T}A$ 不是对角阵，所以， $\hat{x}$ 最好通过公式 $\hat{x}=(A^{T}A)^{-1}A^{T}b$ 来计算。

$\large A=\begin{bmatrix} 1 &1 \\ 1 &3 \\ 1 &5 \end{bmatrix}$ $\large col1=\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$ $\large col2=\begin{bmatrix} 1 \\ 3 \\ 5 \end{bmatrix}$

$\large col1^{T}*col2=9$ $\large A^{T}A=\begin{bmatrix} 1 &1 &1 \\ 1 &3 & 5 \end{bmatrix} \begin{bmatrix} 1 & 1\\ 1& 3\\ 1& 5 \end{bmatrix} = \begin{bmatrix} 3 & 9\\ 9 & 35 \end{bmatrix}$

矩阵A的两个列向量的内积不为0，不正交。且 $A^{T}A$ 不是对角阵。后面，我们为了让 $A^{T}A$ 变成对角阵，把t=(1,3,5)变成了T=(-2,0,2), $A^{T}A$ 也变成了对角阵。

$\large A=\begin{bmatrix} 1 &-2 \\ 1 &0 \\ 1 &2 \end{bmatrix}$ $\large col1=\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$ $\large col2=\begin{bmatrix} -2 \\ 0 \\ 2 \end{bmatrix}$

$\large col1^{T}*col2=0$ $\large A^{T}A=\begin{bmatrix} 1 &1 &1 \\ -2 &0 & 2 \end{bmatrix} \begin{bmatrix} 1 & -2\\ 1& 0\\ 1& 2\end{bmatrix} = \begin{bmatrix} 3 & 0\\ 0 & 8 \end{bmatrix}$

更进一步，如果我们把A中的两个彼此正交的列向量(orthogonal vectors)都变成单位正交向量(orthogonal unit vectors)，则 $A^{T}A$ 会从对角阵变成单位矩阵I。把一个向量变成单位向量的办法是除以这个向量自身的长度。

根据向量长度的计算公式有，列向量col1的长度为根号3，col2的长度为根号8，归一化后有：

$\large \large col1=\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\Rightarrow \large col1_{unit}=\begin{bmatrix} 1/\sqrt{3} \\ 1/\sqrt{3} \\ 1/\sqrt{3} \end{bmatrix}$

$\large col2=\begin{bmatrix} -2 \\ 0 \\ 2 \end{bmatrix}\Rightarrow \large col2_{unit}=\begin{bmatrix} -2/\sqrt{8} \\ 0 \\ 2/\sqrt{8} \end{bmatrix}$

$\large col1_{unit}^{T}*col2_{unit}=0$

得到单位化后的新矩阵 $A_{new}$ ：

$\large A_{new}=\begin{bmatrix} 1/\sqrt{3} & -2/\sqrt{8}\\ 1/\sqrt{3} & 0\\ 1/\sqrt{3} & 2/\sqrt{8} \end{bmatrix}$

和新的方程(注意为了维持原方程组Ax=b中的A变成 $A_{new}$ 后，方程左右两边保持不变，原方程中的x也要改变，变成 $x_{new}=\sqrt{3}C+\sqrt{8}D$ )：

$\large A_{new}x_{new}=\begin{bmatrix} 1/\sqrt{3} &-2/\sqrt{8} \\ 1/\sqrt{3} &0 \\ 1/\sqrt{3}&2/\sqrt{8} \end{bmatrix} \begin{bmatrix} \sqrt{3}C\\ \sqrt{8}D \end{bmatrix}=b$

用这个新矩阵 $A_{new}$ 去计算正规方程中的 $A_{new}^{T}A_{new}$ 得到单位矩阵I：

$\large A_{new}^{T}A_{new}=\begin{bmatrix} 1/\sqrt{3} &1/\sqrt{3} &1/\sqrt{3} \\ -2/\sqrt{8}&0 & 2/\sqrt{8} \end{bmatrix} \begin{bmatrix} 1/\sqrt{3} & -2/\sqrt{8}\\ 1/\sqrt{3}& 0\\ 1/\sqrt{3}& 2/\sqrt{8}\end{bmatrix} = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}$

正规方程左边 $A_{new}^{T}b$ ：

$\large A_{new}^{T}b=\begin{bmatrix} 1/\sqrt{3} &1/\sqrt{3} &1/\sqrt{3} \\ -2/\sqrt{8}&0 & 2/\sqrt{8} \end{bmatrix} \begin{bmatrix} 1\\ 2\\ 4\end{bmatrix} = \begin{bmatrix} 7/\sqrt{3} \\ 6/\sqrt{8} \end{bmatrix}$

最终得到全新的正规方程，这是一个一眼就能得到答案的全新方程组，因为 $A_{new}^{T}A_{new}$ 为方阵，使得原来的正规方程变成：

$\large A^{T}Ax=b\Rightarrow A_{new}^{T}A_{new}x_{new}=A_{new}^{T}b\Rightarrow Ix_{new}=A_{new}^{T}b\Rightarrow x_{new}=A_{new}^{T}b$

最终得到了和原来一样的答案：

$\large \sqrt{3}\hat{C}=7/\sqrt{3}\Rightarrow \hat{C}=7/3$

$\large \sqrt{8}\hat{D}=6/\sqrt{8}\Rightarrow \hat{D}=6/8$

在本例中，归一化后的两个相互正交的列向量 $col1_{new}=(1/\sqrt{3},1/\sqrt{3},1/\sqrt{3})$ 和 $col2_{new}=(-2/\sqrt{8},0,2/\sqrt{8})$ 就是一组标准正交基。现在，我们给出关于标准正交基Orthonormal的正式定义：

如果一组列向量 $q_{1},q_{2},...q_{n}$ ，他们满足彼此之间的内积为0（满足了正交性），且，自己的长度为1（满足了单位化）。则，我们把这样的一组列向量称为标准正交基Orthonomal。同时，我们也把由标准正交基组成的矩阵用大写的英文字母Q来表示。

对于标准正交基而言，一个最常见的例子就是x-y二维坐标系，q1=(1,0)，q2=(0,1)。我们这两个坐标轴不仅垂直，而且，我们还在坐标轴上分别用单位长度标出了每一个刻度。q1和q2共同组成了一个2x2矩阵Q，这是一个2x2的单位矩阵。

对于n维空间，同样有n个坐标轴e1,e2,....en，他们也是一组标准正交基，且他们所组成的矩阵Q也是一个单位阵。

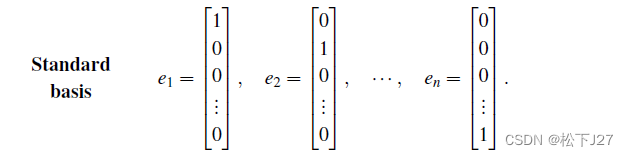
标准正交矩阵(Orthogonal Matrices)

我们把用标准正交基q1,q2...qn所组成的矩阵称为标准正交矩阵Q，Q可以是方阵也可以不是方阵。且， $Q^{T}Q=I$ 。

如果标准正交矩阵Q是一个方阵的话，则这个方阵是满秩的，且秩r=n。则有：

$\large Q^{T}Q=QQ^{T}=I\; and\; Q^{T}=Q^{-1}$

也就是说，如果Q是一个标准正交矩阵，则 $Q^{T}$ 也是一个标准正交矩阵。

例：任何置换矩阵P（permutation）都是一个标准正交矩阵。

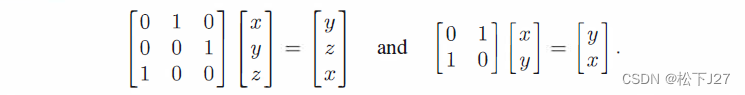
上图的两个置换矩阵，分别交换了(x,y,z)的位置和交换了(x,y)的位置。因为，这两个置换矩阵P的列向量都是单位向量，且彼此两两正交。所以也是标准正交矩阵。

最后，在这里补充一条标准正交矩阵Q的又一条重要性质，即，用一个标准正交矩阵Q去乘一个任意向量都不会改变这个向量的长度。（书上上，这一性质还挺重要的，只是我暂时没发现）

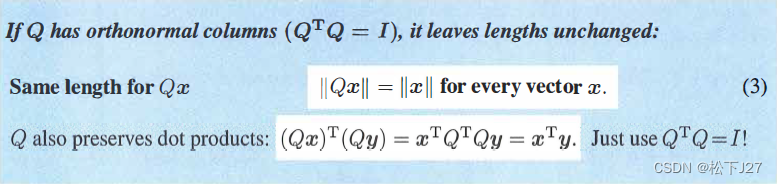
当A为标准正交矩阵时的投影与最小二乘

对于一个mxn的矩阵A，如果矩阵A中的列向量都彼此正交，且向量长度都是1。则A是一个标准正交矩阵。若方程组Ax=b，无解则需要根据最小二乘的计算公式分别计算 $\hat{x}=(A^{T}A)^{-1}A^{T}b$ 和 $p=A\hat{x}=A(A^{T}A)^{-1}A^{T}b$ 。但如果A是标准正交矩阵Q的话，或者说，如果我们先把矩阵A变成标准正交矩阵的话，就能极大的简化最小二乘的计算。

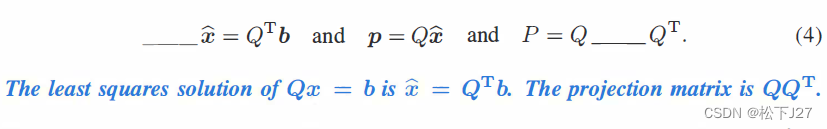
第一：他极大地简化了正规方程的表达式，同时，直接给出了最小二乘解。

$\large A^{T}A\hat{x}=A^{T}b\Rightarrow Q^{T}Q\hat{x}=Q^{T}b\Rightarrow \hat{x}=Q^{T}b$ （正规方程）

第二：他简化了所有包含 $A^{T}A$ 的计算，同时，更重要的是他也避免了求 $A^{T}A$ 的逆。

$\large p=A(A^{T}A)^{-1}A^{T}b\Rightarrow p=Q(Q^{T}Q)^{-1}Q^{T}b \Rightarrow p=QQ^{T}b$ （投影）

$\large P=A(A^{T}A)^{-1}A^{T}\Rightarrow P=Q(Q^{T}Q)^{-1}Q^{T} \Rightarrow P=QQ^{T}$ （投影矩阵）

在代数表达式得到改进的同时，几何表示也得到了相应的改进。根据向量的投影 $p=QQ^{T}b$ ，投影变成了：

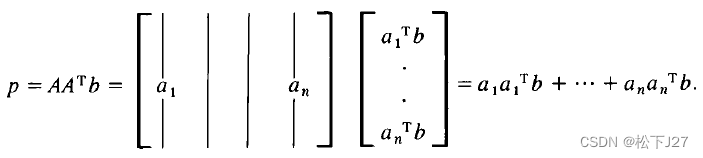
其中：

$a_{1}a_{1}^{T}=\begin{bmatrix} 1 & 0 & . &.& 0\\ 0 & 0 & .&. & .\\ . & . & . & .& .\\ .& . & . & . &. \\ 0& .&. & . &0 \end{bmatrix}$ $a_{2}a_{2}^{T}=\begin{bmatrix} 0 & 0 & . &.& 0\\ 0 & 1 & .&. & .\\ . & . & . & .& .\\ .& . & . & . &. \\ 0& .&. & . &0 \end{bmatrix}$ 依此类推。。。

$a_{n}a_{n}^{T}=\begin{bmatrix} 0 & 0 & . &.& 0\\ 0 & 0 & .&. & .\\ . & . & . & .& .\\ .& . & . & . &. \\ 0& .&. & . &1 \end{bmatrix}$

令b=(b1,b2,...,bn),则有：

$a_{1}a_{1}^{T}b=\begin{bmatrix} 1 & 0 & . &.& 0\\ 0 & 0 & .&. & .\\ . & . & . & .& .\\ .& . & . & . &. \\ 0& .&. & . &0 \end{bmatrix}\begin{bmatrix} b1\\ b2\\ .\\ .\\ bn\\ \end{bmatrix}=\begin{bmatrix} b1\\ 0\\ .\\ .\\ 0\\ \end{bmatrix}$ $a_{2}a_{2}^{T}b=\begin{bmatrix} 1 & 0 & . &.& 0\\ 0 & 0 & .&. & .\\ . & . & . & .& .\\ .& . & . & . &. \\ 0& .&. & . &0 \end{bmatrix}\begin{bmatrix} b1\\ b2\\ .\\ .\\ bn\\ \end{bmatrix}=\begin{bmatrix} 0\\ b2\\ .\\ .\\ 0\\ \end{bmatrix}$ 依此类推。。。

$a_{n}a_{n}^{T}b=\begin{bmatrix} 1 & 0 & . &.& 0\\ 0 & 0 & .&. & .\\ . & . & . & .& .\\ .& . & . & . &. \\ 0& .&. & . &0 \end{bmatrix}\begin{bmatrix} b1\\ b2\\ .\\ .\\ bn\\ \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ .\\ .\\ bn\\ \end{bmatrix}$

用几何图像来表示就是：

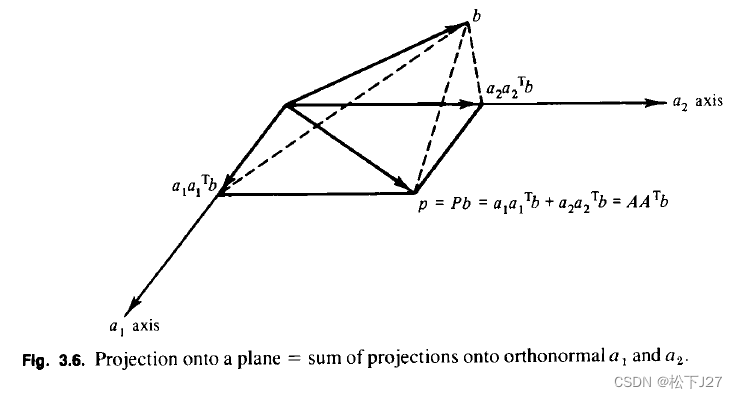
也就是说，向量b在A所张成的列空间上的投影p等于，b在每个坐标轴上的投影的和。

此外，当A为标准正交矩阵时（当A为方阵时,m=n），A中的列向量可以张满整个 $R^{n}$ 。A中的每个列向量，实际上就是n维正交坐标系中的每个轴所对应的单位向量。对于 $R^{n}$ 中的任意一个向量b，b在A的列空间内，所以可以写成Ax=b的形式，x中的每个元素都是A中各列所对应的权重。当A为Q时，我们把Qx=b写成如下形式：

q1,q2,...,qn分别表示n维坐标系中的每个坐标轴上的单位向量，这样一来，上式所表示的就是，在n维直角坐标系中，任意一个向量b等于，他在q1轴，q2轴，。。。qn轴上分量的和。

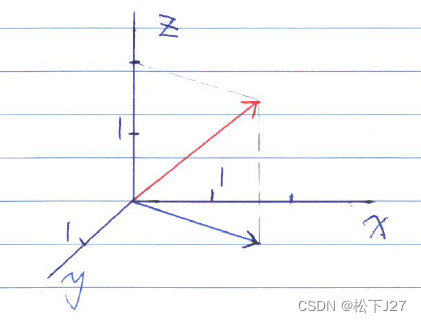
例如：

$\large Qx\; \begin{bmatrix} 1 &0 &0 \\ 0 & 1 &0 \\ 0 &0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z \end{bmatrix}=\begin{bmatrix} x\\ y\\ z \end{bmatrix}\; b$