动态规划概述
动态规划的两个要求:
1.最优子结构
例:现有一座10级台阶的楼梯,我们要从下往上走,每次只能跨一步,一步可以往上走1级或者2级台阶,请问一共有多少种解法呢?
| 台阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 走法数 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 |
可以发现,我们都可以通过前两个状态来推出当前状态
**最优子结构:**大问题的(最优)解可以由小问题的(最优)解来推出,在这个问题当中,大问题的f(n)的解可以由小问题f(n-2)和f(n-1)的解推出。注意:在问题拆解过程当中不能无限递归
2.无后效性
未来与过去无关,一旦得到了一个小问题的解,如何得到它的解的过程不会影响到大问题的求解。在上面这个问题种,我们只需要知道f(n-1)和f(n-2)的值,但是怎么得到它的已经不重要了。
动态规划的两个元素:
状态:
求解过程进行到了哪一步,可以理解为一个子问题。
转移:
从一个状态(小问题)的(最优)解推导出另一个状态(大问题)的(最优)解的过程。
最短路I
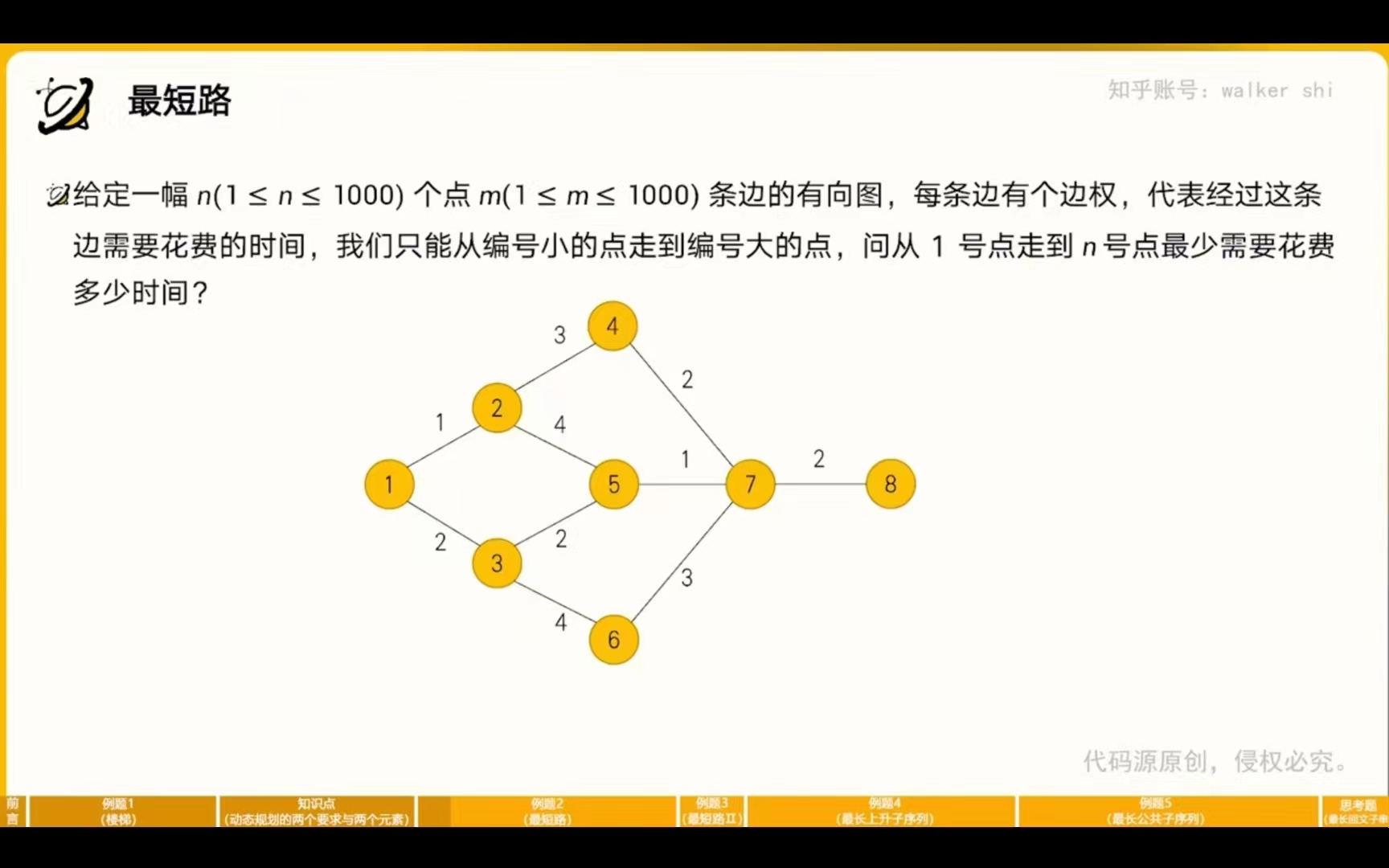
最优子结构:为了计算出从1号点到y号点最少花费的时间,我们可以计算出所有与y号点所连接的边,并且标记所有小于y的点x,从1号点到x号点所花费的最短时间,最后再推到y号点的情况。
无后效性:我们只关心每个点所花费的最短时间,不关心到底是怎么走到这个点的。
状态:f[i]表示从1到i所花费的最短时间
转移:假设已经知道了f[x]的值,并且存在一条从x到y的代价为z的边,那么可以推导出方程:f[y]=min(f[y],f[x]+z)
AC代码:
#include<iostream>
using namespace std;
const int N = 1010;
int a[N][N], f[N], n, m;//a数组存图
int main(void)
{
cin >> n >> m;
memset(a, 127, sizeof(a));//将a的每一条边都初始化为一个很大的值
for (int i = 1; i <= m; i++)
{
int x, y, z;
cin >> x >> y >> z;
a[x][y] = min(a[x][y], z);//防止有重边
}
memset(f, 127, sizeof f);
f[1] = 0;
for (int i = 2; i <= n; i++)
{
for (int j = 1; j < i; j++)
{
if (f[j] < 1 << 30 && a[j][i] < 1 << 30)
f[i] = min(f[i], f[j] + a[j][i]);
}
}
cout << f[n];
return 0;
}
最短路II
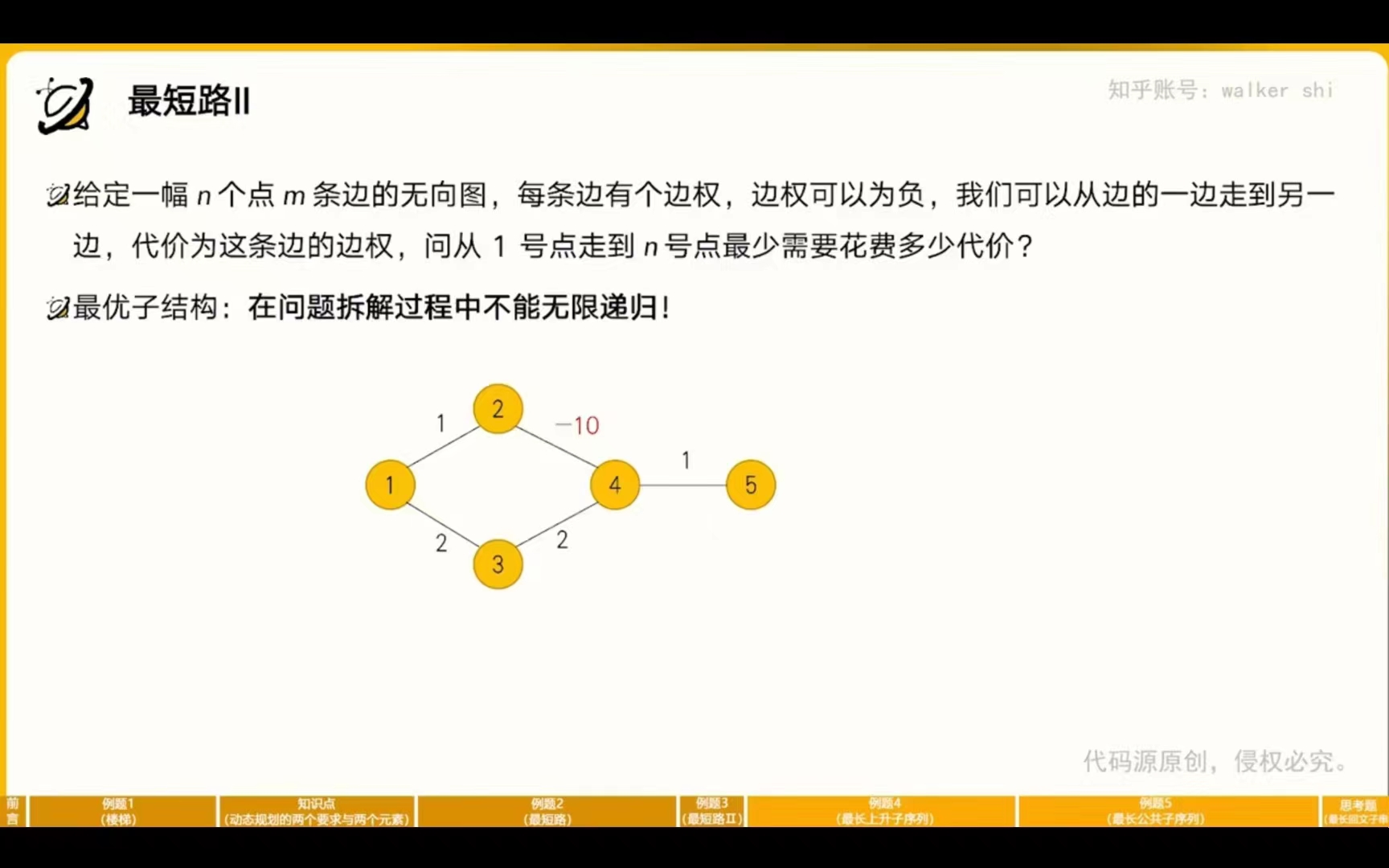
这里存在无限递归,因为每一次绕着1 2 4 3走一圈代价就会减少5,所以不能使用动态规划解决
最长上升子序列

最优子结构:为了计算a[i]以i结尾的最长上升子序列的长度,我们可以通过枚举所有小于i的位置j,我们可以先计算出以a[j]结尾的上升子序列,然后判断a[i]是否大于a[j],如果a[i]>a[j]那么答案就是a[j]+1,反之答案就是a[j]。
无后效性:我们只关心以i这个位置结尾的最长上升子序列的长度,并不关心子序列是什么。
状态:用f[i]表示以i结尾的最长上升子序列的长度
转移:对于某个位置i,为了计算i,我们枚举子序列种所有小于i的元素j,满足j<i&&a[j]<a[i]可以得到状态转移方程:f[i]=max(f[i],f[i]+1)。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | 13 | 14 | 17 | 12 | 7 | 8 | 19 | 23 | 52 | 11 | 6 | 9 | 15 | 520 | 1314 | 10 |
| f | 1 | 2 | 3 | 1 | 1 | 2 | 3 | 4 | 5 | 3 | 1 | 3 | 4 | 6 | 7 | 4 |
最后答案等于f[i]当中的最大值
AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, a[N], f[N];
int main(void)
{
cin >> n;
int res = -10;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++)
{
f[i] = 1;//如果没有找到能够满足子序列的,那么它的f[i]值就是1,需要初始化一下
for (int j = 1; j < i; j++)
{
if (a[j] < a[i])
{
f[i] = max(f[i], f[j] + 1);
if (f[i] > res) res = f[i];
}
}
}
cout << res;
return 0;
}
最长公共子序列

最优子结构:为了计算出a[i]和b[j]的最长公共子序列,可以从a[i-1]和a[j-1]来转移过来。
假如a[i]==a[j]那么我们可以从f[i-1][j-1]+1转移过来,就是考虑a的前i个元素和b的前j个元素
假如a[i]!=a[j]那么可以从f[i-1][j]和f[i][j-1]转移过来,就是考虑a的前i-1个元素和b的前j个元素以及a的前i个元素和b的前j-1个元素。
这时候可能就有人会有疑问,为什么不考虑f[i-1][j-1]的情况呢?
举一个例子:
| a: | A | D | A | B | C | A | B | C | D |
|---|---|---|---|---|---|---|---|---|---|
| i | |||||||||
| b: | D | B | A | B | C | C | D | A | B |
| j |
如上面的这个表格,如果a[i]!=a[j]那么有没有i和j的元素,对前面的子串都是没有影响的。
串a是ADABCA和ADABC与DBABCC去比较都是一样的,所以f[i-1][j-1]的这种情况已经被包含在
f[i-1][j]和f[i][j-1]当中了。
无后续性:我们只在乎最长公共子序列的长度是多少,至于是哪些元素构成的我们并不在乎
状态:f[i][j]表示a以第i个位置结尾和b以第j个位置结尾的最长公共子序列是多少。
转移:如果a[i]==a[j]那么f[i][j]=f[i-1][j-1]+1。
如果a[i]!=a[j]那么f[i][j]max(f[i-1][j],f[i][j-1])
AC代码:
#include<iostream>
using namespace std;
const int N = 1010;
int n, m, a[N], b[N], f[N][N];
int main(void)
{
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= m; i++) cin >> b[i];
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
}
cout << f[n][m] << endl;
return 0;
}
思考题:最长回文子串
状态:f[i][j]表示从i到j是否满足回文,如果f[i][j]要满足回文字符串的条件,我们可以从
f[i+1][j-1]推到过来,如果f[i+1][j-1]满足回文子串,那么只要str[i==str[j],就可以判定
f[i][j]是回文字符串, 那么如何去得到f[i+1][j-1]的状态呢,我们可以通过不断改变字符串的长度,来判断不同长度字符串的所有情况是否满足是回文子串,比如我要看是否存在长度为4的回文字符串,那么就可以先去找长度为2的,最后判断边界是否相等(str[i]==str[j])即可。
转移:如果str[i]==str[j]那么 f[i][j]=f[i+1][j-1],反之f[i][j]=false。
AC代码:
#include<iostream>
using namespace std;
const int N = 1010;
bool f[N][N];
int main(void)
{
string str;
cin >> str;
int len = str.size();
for (int i = 0; i <= len; i++)
{
f[i][i] = true;//将一个字符的全都初始化为true
}
int begin = 0,maxlen=-10010;
for (int l = 2; l <= len; l++)//从长度为2开始计算状态,找到满足回文的子串
{
for (int i = 0; i < len; i++)
{
int j = l + i - 1;
if (j >= len) break;
if (str[i] != str[j]) f[i][j] = false;
else
{
if (j - i < 3)
{
f[i][j] = true;
}
else
{
f[i][j] = f[i + 1][j - 1];
}
}
if (f[i][j] && j - i + 1 > maxlen)
{
maxlen = j - i + 1;
begin = i;
}
}
}
cout << str.substr(begin, maxlen);
return 0;
}