🚀write in front🚀
📜所属专栏：初阶数据结构
🛰️博客主页：睿睿的博客主页
🛰️代码仓库：🎉VS2022_C语言仓库
🎡您的点赞、关注、收藏、评论，是对我最大的激励和支持！！！
关注我，关注我，关注我，你们将会看到更多的优质内容！！

前言

  在前面的学习中，我们实现了栈与队列的实现。今天我们就通过顺序表来实现二叉树！

一. 二叉树的顺序结构

我们如何让顺序表和二叉树建立联系呢？

我们可以先对二叉树的每个结点进行编号，通过数组的连续排列建立以下联系：

这样我们就可以通过数组的下标来模拟实现二叉树了！

但是普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。

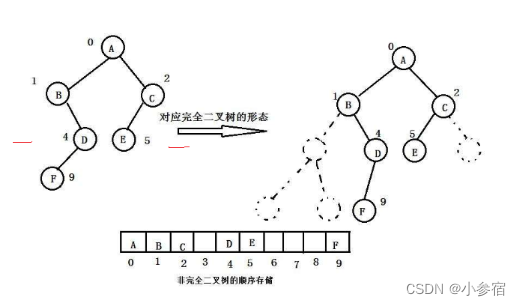
所以我们的数组存储表示二叉树只适合完全二叉树。

二.堆的概念及结构

简单的来说，堆就是一颗完全二叉树，并且有以下性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

其中分为小根堆和大根堆：

小根堆：

树中所有父亲都小于等于孩子：

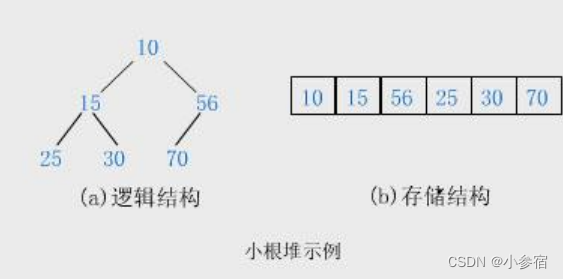
大根堆：

树中所有父亲都大于等于孩子

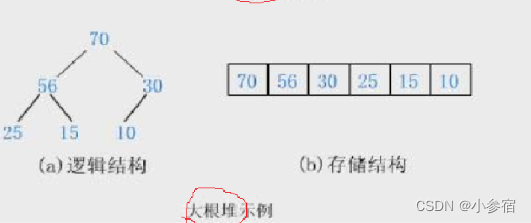
注意：

在数据结构里面我们所学的栈，堆都是一种数据结构，他们与操作系统
中的栈和堆是两回事，一个是数据结构，一个是操作系统相关的知识，一定不要搞混淆！

三.堆的实现：

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

void HeapInit(HP* php);
void HeapDestroy(HP* php);

void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);

void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int n, int parent);

1.堆的插入(向上调整算法）：

  先插入一个数到数组的尾上，再进行向上调整算法，直到满足堆。

向上调整算法的条件是：
除了child结点，之前的结点都是堆

代码实现：

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] > a[parent])
		{
			swap(&a[child],&a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->capacity == php->size)
	{
		HPDataType* ptr = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
		if (ptr == NULL)
		{
			perror("realloc::fail");
			return;
		}
		php->a = ptr;
		php->capacity *= 2;
	}
	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size-1);
}

2.堆的删除（向下调整算法）：

  在这里删除堆是指删除堆顶的数据，因为删除堆尾元素没有什么实际的意义。将堆顶的数据与最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

向下调整算法的条件是：

左右子树都为堆！

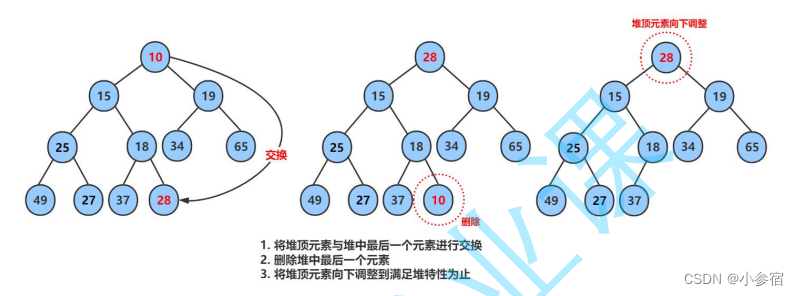
代码实现：

void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	// 删除数据
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 选出左右孩子中大的那一个
		if (child + 1 < n && a[child+1] > a[child])
		{
			++child;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

3.堆的构建：

这里建议把后面的堆排序看了在来看这段代码：

void HeapInitArray(HP* php, int* a, int n)
{
	assert(php);

	php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (php->a == NULL)
	{
		perror("malloc fail");
		return;
	}

	php->size = n;
	php->capacity = n;

	// 建堆
	for (int i = (n-2)/2; i >= 0; --i)
	{
		AdjustDown(php->a, php->size, i);
	}
}

这里的意思是给你一个属数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。

三.堆的应用：

1.堆排序：

  通过上面的学习我们发现，堆有排序的功能。但是如果我们要通过每次建堆的方式来排序，那还是挺浪费空间的。为什么不在原有的数组里面进行堆排序呢？
堆排序即利用堆的思想来进行排序，总共分为两个步骤：

1. 建堆
   升序：建大堆
   降序：建小堆
2. 利用堆删除思想来进行排序

  在这里会有同学问道，根据堆的性质，大堆不就是降序，小堆不就是升序吗？为什么升序要建大堆，降序要建小堆呢？

  其实啊，我们的堆在数组中的排序并不是完全的。对于升序，如果我们非要通过建小堆来排序，只能通过拿走堆顶，然后将剩下的元素进行重新建立大堆的方式来寻找第二小的元素，这样的时间效率会非常低，而且过程非常的麻烦。

那么我们应该怎么做呢？

步骤1：建堆：

向上调整建堆：

  向上调整建堆就相当于堆的插入，在原数组的空间里，每插入一个数，就向上调整一遍，代码如下：

void Heapsort(HPDataType* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		AdjustUp(a, i);
	}
}

当然我们可以来看看这种方法的时间复杂度：

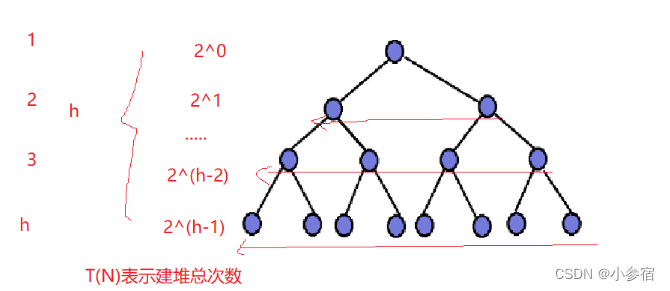
通过求和：

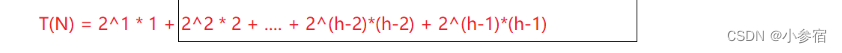
通过错位相减法可以得到：

由此可见，向上调整建堆的时间复杂度为O(N*logN)

向下调整建堆：

  既然我们可以向上调整建堆，能不能向下调整建堆呢？答案是肯定的，只要我们找到最后一个叶子结点的父结点，把该结点及该结点以前的结点向下调整，这样就可以很好的建堆了。代码如下：

//向下调整建堆
	for (int i = (n - 2) / 2; i > 0; i--)
	{
		AdjustDown(a, n,i);
	}

时间复杂度：

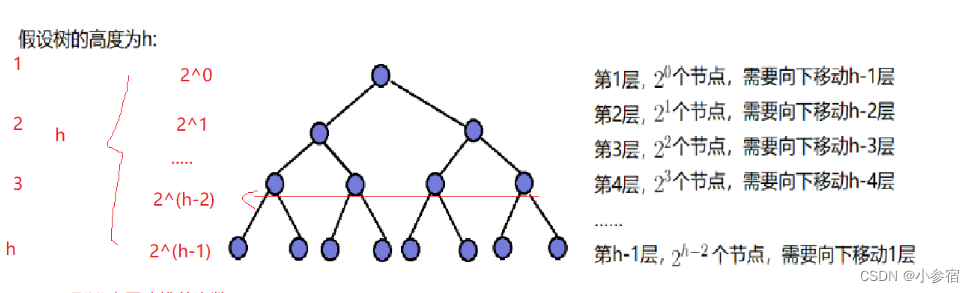
同样的我们通过求和可以得到以下结果：

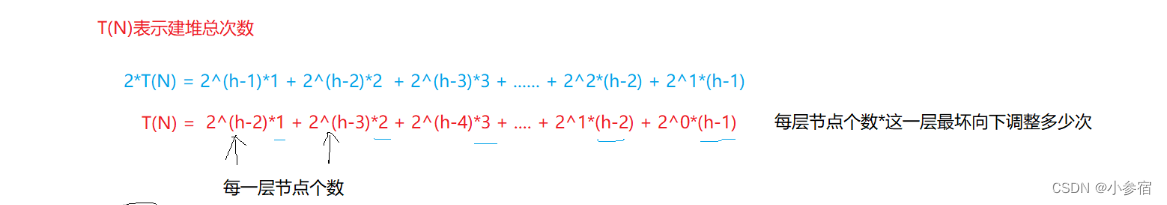
通过错位相减得到：

所以向下调整算法的时间复杂度为O（N)。

步骤2：堆删除思想：

  以升序为例，在我们建完大堆之后，将大堆的第一个元素和最后一个元素交换位置，让size- -，随后将堆进行向下调整（这里就是堆删除的思想）即可。在向下调整的过程中就会将第二大的元素调整到第一个元素，随后在将第一个元素和倒数第二个元素交换……以此循环即可实现排序：

void Heapsort(HPDataType* a, int n)
{
	//向上调整建堆
	for (int i = 0; i < n; i++)
	{
		AdjustUp(a, i);
	}
	//向下调整建堆
	for (int i = (n - 2) / 2; i > 0; i--)
	{
		AdjustDown(a, n,i);
	}
	//堆删除

	int end = n - 1;
	for (int i = end; i > 0; i--)
	{
		swap(&a[i], &a[0]);
		end--;
		AdjustDown(a, end, i);
	}

}

建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

  其实上面的时间复杂度可以很明显的看出向下调整算法的O(N)更小，因为向上调整算法是更多的结点调整更多次，向下调整算法是更少的结点调整更多次，所以向下调整算法的时间复杂度更小。

2.TOP-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能全部加载到内存中)。

顺便来复习一下单位的换算：

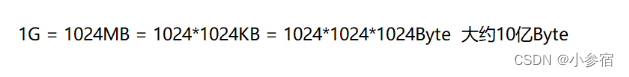
最佳的方式就是用堆来解决，基本思路如下：

假设我们要从N个元素取最大/最小的K个元素

1. 用数据集合中前K个元素来建堆
   前k个最大的元素，则建小堆
   前k个最小的元素，则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素

我们以寻找最大的前k个数为例：

我们先通过文件操作进行造数据：
忘记文件操作的朋友们可以看看这篇博客 文件操作（上）

void CreateNdata()
{
	const char* file = "data.txt";
	FILE* fq = fopen(file, "w");
	if (fq == NULL)
	{
		perror("malloc::fail");
		return;
	}
	srand(time(NULL));

	int n = 10000000;
	for (int i = 0; i < n; i++)
	{
		int ret = rand() % 10000;
		fprintf(fq, "%d\n", ret);
	}

	fclose(fq);
	free(fq);

}

大家会发现我们造的数据非常多，没错，就是要这种效果，现实生活中数据过多我们就不能用内存来存储，用文件来储存。

接下来我们将这些数据的前k个进行建堆，并将剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素。一定要记得建的是小堆！

void PrintTopK(const char* file, int k)
{
	// 1. 建堆--用a中前k个元素建小堆
	int* topk = (int*)malloc(sizeof(int) * k);
	assert(topk);
	FILE* fq = fopen(file, "r");
	if (fq == NULL)
	{
		perror("malloc:fail");
		return;
	}

	for (int i = 0; i < k; i++)
	{
		fscanf(fq, "%d", &topk[i]);
	}
	//建小堆
	for (int i = (k - 2) / 2; i >= 0; i--)
	{
		AdjustDown(topk, k, i);
	}
	int val = 0;
	//ret是fscanf的返回值，fscanf返回eof，则结束
	int ret = fscanf(fq, "%d", &val);
	while (ret != EOF)
	{
		if (val > topk[0])
		{
			swap(&val ,&topk[0]);
			AdjustDown(topk, k, 0);
		}
		ret = fscanf(fq, "%d", &val);
	}

	for (int i = 0; i < k; ++i)
	{
		printf("%d ", topk[i]);
	}
	printf("\n");

	fclose(fq);
	free(fq);
}

随后我们看看结果：
先创建数据：

int main()
{
	CreateNdata();
	//PrintTopK("data.txt", 10);
}

然后在取前k个数据：

int main()
{
	//CreateNdata();
	PrintTopK("data.txt", 10);
}

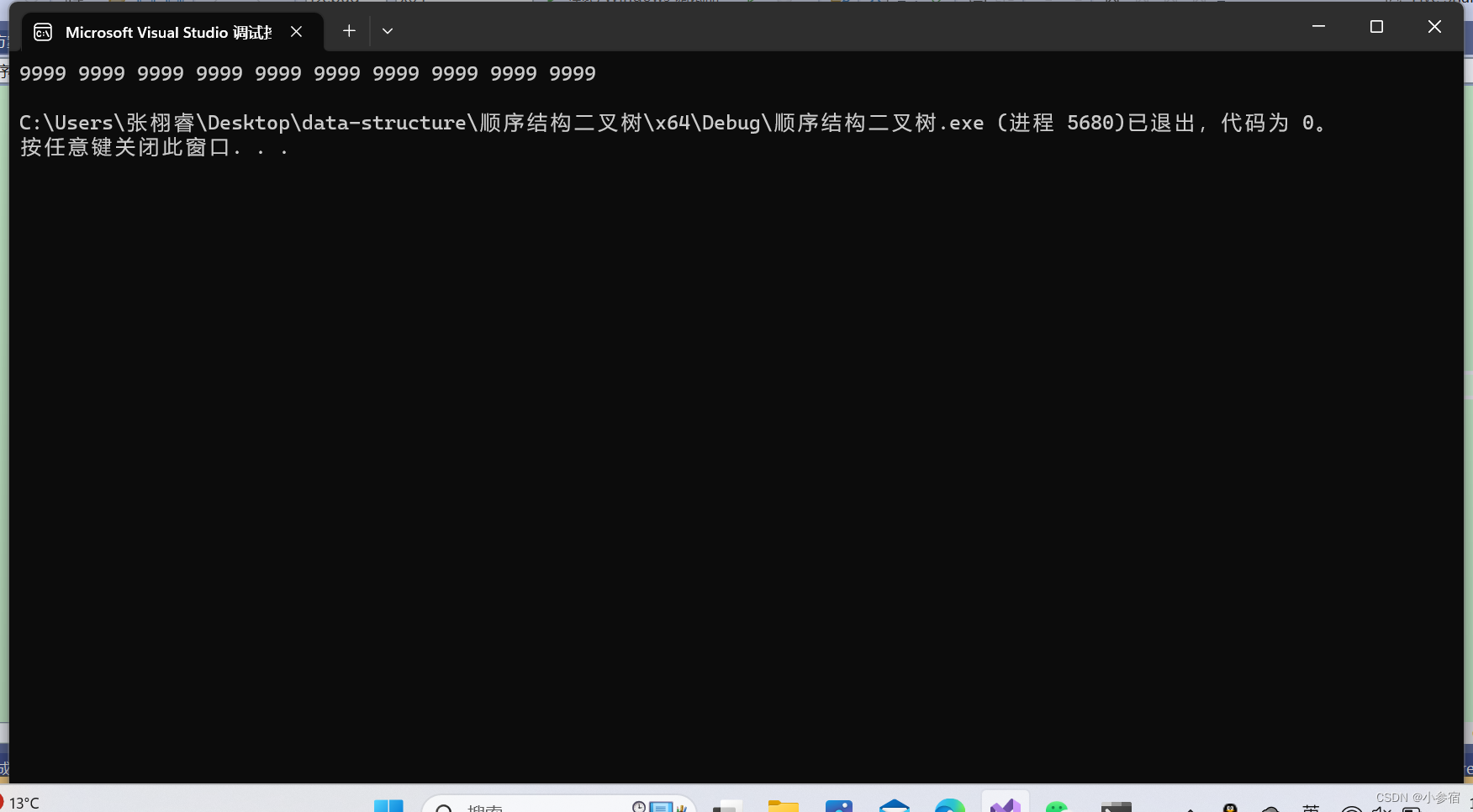
产生这个结果的原因是数据太多了，导致产生随机数9999的数据太多了。现在我们直接改改文件里的数据：

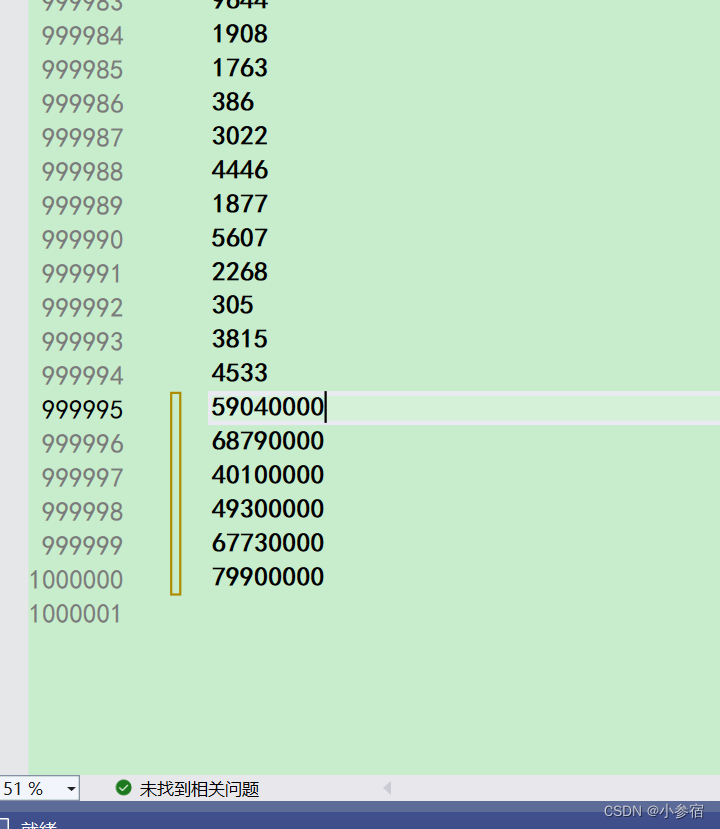
在改了以后最大的几个数一定会有最后几个，现在我们来看看结果：

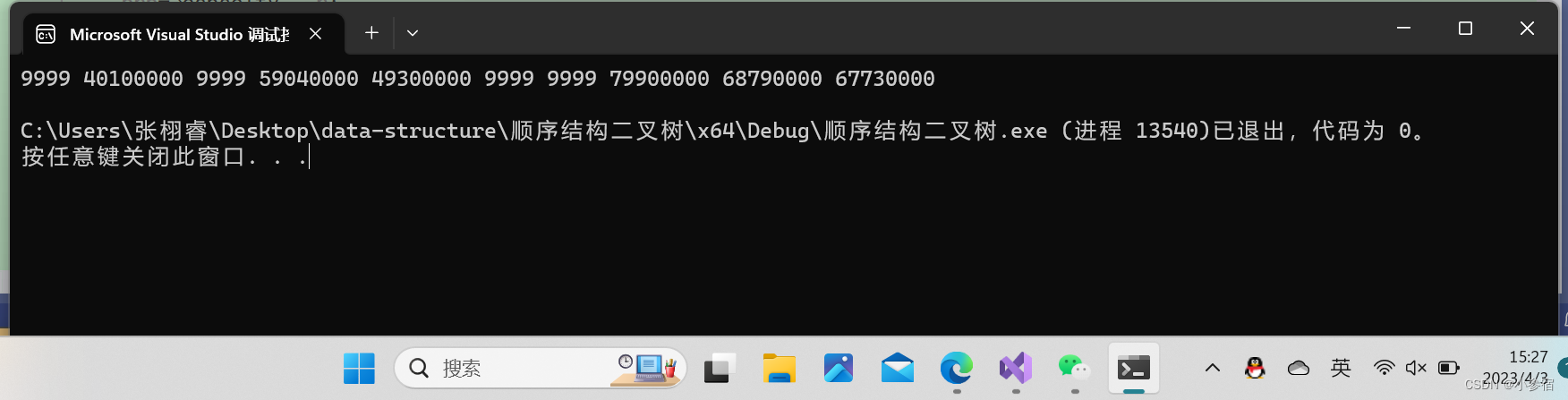
这样最大的前k个数就以小堆的形式打印出来了。

总结

  更新不易，辛苦各位小伙伴们动动小手，👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要！最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！

专栏订阅：
每日一题
c语言学习
算法
智力题
初阶数据结构
更新不易，辛苦各位小伙伴们动动小手，👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要！最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！