(十）排序算法-冒泡排序

news2024/7/6 19:05:34

1 排序算法

1.1 介绍

排序也称为排序算法（Sort Algorithm），排序是将一组数据，依指定的顺序进行排列的过程。

1.2 排序的分类

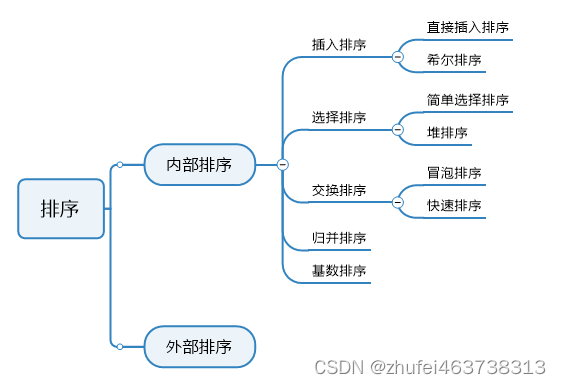
（1）内部排序
指将需要处理的所有数据都加载到内部存储器中进行排序。
（2）外部排序法
数据量过大，无法全部加载到内存中，需要借助外部存储进行排序。
（3）常见的排序算法分类
在这里插入图片描述

2 冒泡排序

2.1 基本介绍

冒泡排序是一种简单的排序算法，它也是一种稳定排序算法。其实现原理是重复扫描待排序序列，并比较每一对相邻的元素，当该对元素顺序不正确时进行交换。一直重复这个过程，直到没有任何两个相邻元素可以交换，就表明完成了排序。
冒泡排序（Bubble Sorting）的基本思想是：通过对待排序序列从前向后（从下标较小的元素开始），依次比较相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部，就像水底的气泡一样逐渐向上冒。
因为排序的过程中，各元素不断接近自己的位置，如果一趟比较下来没有进行过交换，就说明序列有序，因此要在排序过程中设置一个标志 flag 判断元素是否进行过交换。从而减少不必要的比较。
动画展示：
在这里插入图片描述

假设待排序序列为 (5,1,4,2,8)，如果采用冒泡排序对其进行升序（由小到大）排序，则整个排序过程如下所示：
（1）第一轮排序，此时整个序列中的元素都位于待排序序列，依次扫描每对相邻的元素，并对顺序不正确的元素对交换位置，整个过程如下所示。
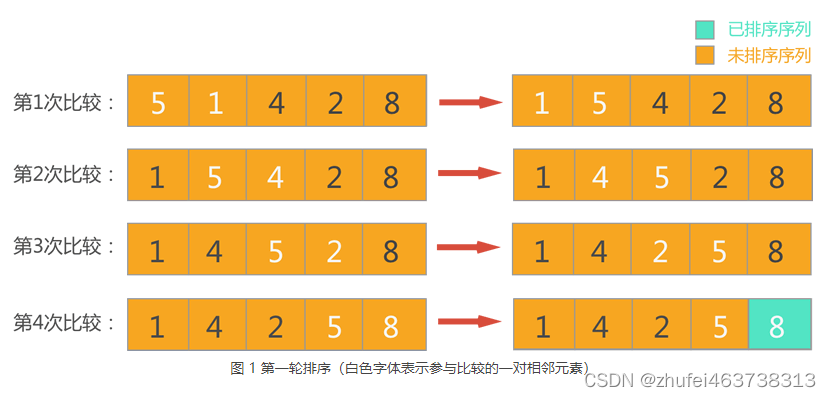
在这里插入图片描述
从上图可以看到，经过第一轮冒泡排序，从待排序序列中找出了最大数 8，并将其放到了待排序序列的尾部，并入已排序序列中。

（2）第二轮排序，此时待排序序列只包含前 4 个元素，依次扫描每对相邻元素，对顺序不正确的元素对交换位置，整个过程如下图所示。
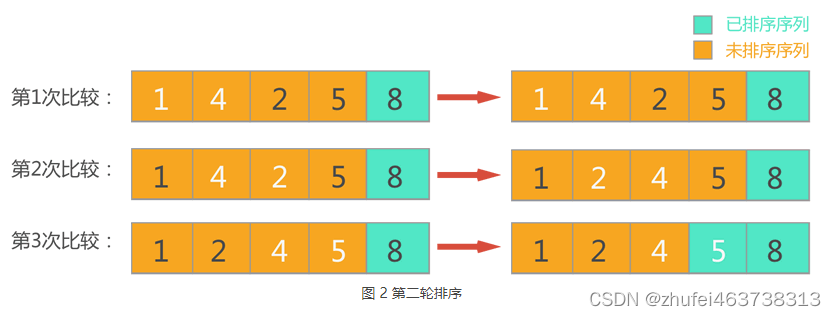
在这里插入图片描述
可以看到，经过第二轮冒泡排序，从待排序序列中找出了最大数 5，并将其放到了待排序序列的尾部，并入已排序序列中。
（3）第三轮排序，此时待排序序列包含前 3 个元素，依次扫描每对相邻元素，对顺序不正确的元素对交换位置，整个过程如下图所示。
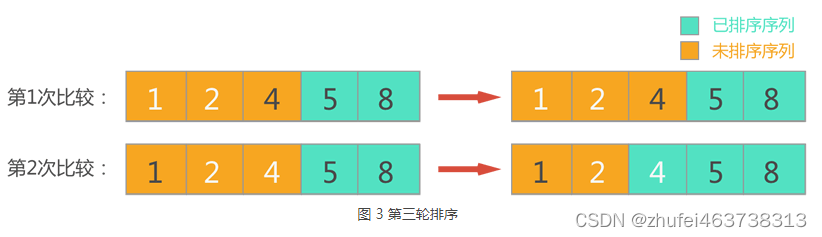
在这里插入图片描述
经过本轮冒泡排序，从待排序序列中找出了最大数 4，并将其放到了待排序序列的尾部，并入已排序序列中。
（4）第四轮排序，此时待排序序列包含前 2 个元素，对其进行冒泡排序的整个过程如下图所示。
在这里插入图片描述经过本轮冒泡排序，从待排序序列中找出了最大数 2，并将其放到了待排序序列的尾部，并入已排序序列中。
（5）当进行第五轮冒泡排序时，由于待排序序列中仅剩 1 个元素，无论再进行相邻元素的比较，因此直接将其并入已排序序列中，此时的序列就认定为已排序好的序列。
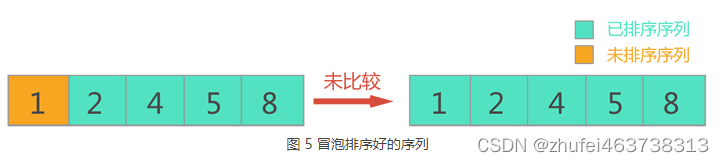
在这里插入图片描述

2.1 代码实现

/**
 * 冒泡排序
 */
public class BubbleSort {
    public static void main(String[] args) {
        /*int[] arr = {3, 9, -1, 10, -2,20,30};

        System.out.println("-----------排序前-----------");
        System.out.println(Arrays.toString(arr));

        bubbleSort(arr);
        System.out.println("-----------排序后-----------");
        System.out.println(Arrays.toString(arr));*/

        // 测试
        // 创建80000个随机的数组
        int[] arr = new int[80000];
        for (int i = 0; i < 80000; i++) {
            arr[i] = (int) (Math.random() * 80000);
        }

        System.out.println("-----------排序前-----------");
        System.out.println(Arrays.toString(arr));

        bubbleSort(arr);
        System.out.println("-----------排序后-----------");
        System.out.println(Arrays.toString(arr));





    }

    public static void bubbleSort(int [] arr){
        // 临时变量
        int temp = 0;
        boolean flag = false;
        for (int i = 0; i < arr.length - 1; i++) {
            flag = true;
            for (int j = 0; j < arr.length - 1 - i; j++) {
                // 如果前面的数比后面的数大，则交换
                if (arr[j] > arr[j + 1]) {
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    flag = false;
                }
            }
            if(flag){
                break;
            }
        }
    }
}