目录

Split()分隔字符串

StringBuilder用法

反转字符串中的单词

LocalDate用法

LocalDate类具体方法 

查询年月日

 修改时间

 判断日期先后，是否是闰年，月份年份长度

 对时间进行加减操作

跑步锻炼 

 使用LoaclDate解法

没使用LocalDate解法

next()和nextLine()的区别

BigInteger用法

java String类型与BigInteger类型互转

回溯算法

解决排序，子集合问题

全排列

题目-删除字符

解法一：使用栈

解法二：使用集合（原理和栈一致）

题目-不同字符的最小子序列

 解法一：使用栈

动态规划

斐波那契数

数组解法-时间复杂度O(n)

 解法二：时间复杂度O(n)

题目-零钱兑换

位运算操作

最小公约数、公倍数

二分查找

高效求素数

正则匹配

---

 前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站前言 – 床长人工智能教程https://www.cbedai.net/gkbskc

Split()分隔字符串

Java中split主要用于分隔字符串，十分的常用

具体分析如下: 

1、如果用“.”作为分隔的话,必须是如下写法,String.split("\\."),这样才能正确的分隔开,不能用String.split(".")。

2、如果用“|”作为分隔的话,必须是如下写法,String.split("\\|"),这样才能正确的分隔开,不能用String.split("|")，“.”和“|”都是转义字符,必须得加"\\"。

3、如果在一个字符串中有多个分隔符,可以用“|”作为连字符,比如,“acount=? and uu =? or n=?”,把三个都分隔出来,可以用String.split("and|or")。

StringBuilder用法

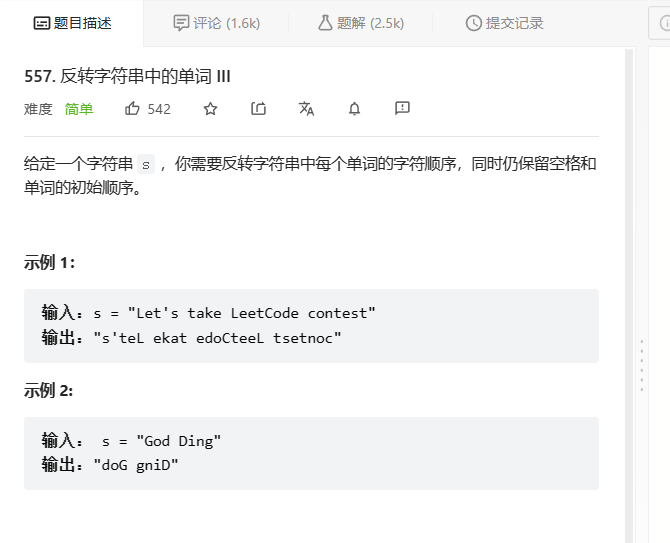
反转字符串中的单词

反转字符中的单词

class Solution {
    public String reverseWords(String s) {
        String str[]=s.split(" ");
         StringBuilder res= new StringBuilder();
        for(int i=0;i<str.length;i++){
             StringBuilder sb=new StringBuilder(str[i]);
            res.append(sb.reverse().append(" "));
            sb.delete(0,sb.length());
        }
        return res.toString().trim();
    }
}

LocalDate用法

学习了LocalDate类，他适合处理日期星期问题

在import java.time.LocalDate;包下

//获取当前时间
LocalDate localDate = LocalDate.now();
//输入年月日设置时间
LocalDate localDate = LocalDate.of(year,month,day);

LocalDate类具体方法 

查询年月日

 修改时间

 判断日期先后，是否是闰年，月份年份长度

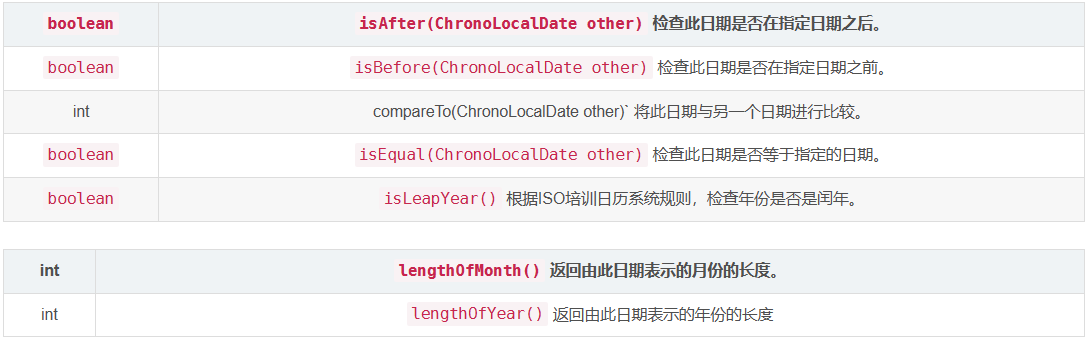
 对时间进行加减操作

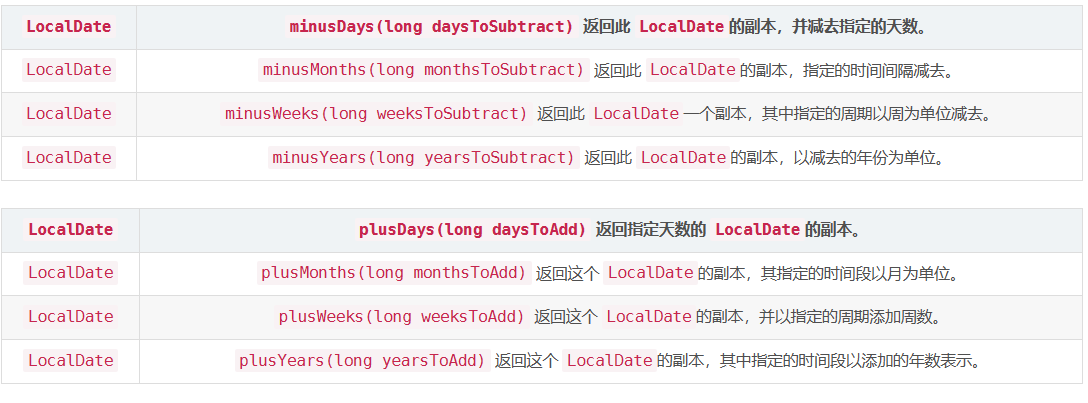
跑步锻炼 

跑步锻炼

 使用LoaclDate解法

import java.util.Scanner;
import java.time.LocalDate;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        LocalDate sd=LocalDate.of(2000,1,1);
        LocalDate ad=LocalDate.of(2020,10,1);
        int sum=0;
        while(true){
        
          if(sd.getDayOfMonth()==1||sd.getDayOfWeek().getValue()==1){
            sum+=2;
          }else{
            sum+=1;
          }
            if(sd.isEqual(ad)){
            System.out.println(sum);break;
           }
          sd=sd.plusDays(1);
        }
        scan.close();
    }
}

没使用LocalDate解法

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
      public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int arrMonth[]={0,31,28,31,30,31,30,31,31,30,31,30,31};
        int runSum=0;int month=12;int week=6;
        for(int i=2000;i<=2020;i++){
            if(i==2020)month=9;//2020年只算到9月就行
            for(int j=1;j<=month;j++){
                int monthDaySum=isHowDaysMonth(i,j,arrMonth);//看这年的这个月有多少天
                for(int k=1;k<=monthDaySum;k++){
                    if((k==1)||(week==1))runSum+=2;//周日或者月初
                    else runSum+=1;
                    week++;
                    if (week>7){
                        week=1;
                    }
                   // System.out.println(runSum);
                }
            }
        }
        runSum+=2;//加上10月1的两千米
        System.out.println(runSum);
        scan.close();
    }


    public static int isHowDaysMonth(int year,int month,int arrMonth[]){
        boolean runYear = isRunYear(year, arrMonth);
//        if (runYear)System.out.println(year+"是闰年"+arrMonth[2]);
//        else System.out.println(year+"不是闰年"+arrMonth[2]);
        return arrMonth[month];
    }

    public static boolean isRunYear(int year,int arrMonth[]){
        if((year%400==0)||(((year%4==0)&&(year%100!=0)))){
            arrMonth[2]=29;
            return true;
        }
        arrMonth[2]=28;
        return false;
    }
}

next()和nextLine()的区别

2、回车符之间的区别

　其实我么发现next(),nextInt()和nextFloat()看到空格符或回车符都认为读取结束，此时不会读取回车符。
    意思就是回车符只会留在这里等待下一个可以读取回车符号的读取流来把这个回车符接收掉
　nextLine()也是以回车符为结束，并且只是以回车符结束,并且会读取回车符
 

Math.pow(n,m)为n的m次方

Math.pow(n,1.0/m)为开n的m次方

System.out.printf("%.3f",Math.pow(16.0, 1.0 / 3));保留三位小数，运算结果会四舍五入

BigInteger用法

所在包

import java.math.BigInteger

1. 赋值：

BigInteger a=new BigInteger("1");           // 字符

BigInteger b=BigInteger.valueOf(1);        // 整型

2. 运算

① add(); 大整数相加

BigInteger a=new BigInteger(“23”);

BigInteger b=new BigInteger(“34”);

a. add(b);

②subtract(); 相减

③multiply(); 相乘

④divide(); 相除取整

⑤remainder(); 取余

⑥pow(); a.pow(b)=a^b

⑦gcd(); 最大公约数

⑧abs(); 绝对值

⑨negate(); 取反数

⑩mod(); a.mod(b)=a%b=a.remainder(b);

b.bitLength()//求二进制位数

java String类型与BigInteger类型互转

        String a = "123456789";
        //String转为BigInteger
        BigInteger b=new BigInteger(a);
        //BigInteger转为String
        String c = String.valueOf(b);

蓝桥杯题 梅森素数

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
import java.math.BigInteger;
public class Main {
     public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码..
        BigInteger bigInteger=new BigInteger("2");//赋初始值
        BigInteger subtract = bigInteger.pow(11213).subtract(BigInteger.valueOf(1));//bigInteger-1
        String str=String.valueOf(subtract);//转为字符串
        System.out.println( str.substring(str.length()-100));//取最后一位

    }
}

回溯算法

解决排序，子集合问题

组合总和

class Solution {
    List<List<Integer>> res=new LinkedList<>();
    LinkedList<Integer> track=new LinkedList<>();
    int sum=0;
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
       if(candidates.length==0)return res;
         backtrack(candidates,target,0);
        return res;
    }

    void backtrack(int[] candidates, int target,int start){
         if(sum==target){
             res.add(new LinkedList<>(track));
             return ;
         }
         if(sum>target)return;
         for(int i=start;i<candidates.length;i++){
             sum+=candidates[i];
             track.add(candidates[i]);
             backtrack(candidates,target,i);
             sum-=candidates[i];
             track.removeLast();
         }
    }
}

   for(int i=start;i<candidates.length;i++){
             sum+=candidates[i];
             track.add(candidates[i]);
             backtrack(candidates,target,i);//还是从i开始，表示可复选的  
             sum-=candidates[i];
             track.removeLast();
         }

   for(int i=start;i<candidates.length;i++){
             sum+=candidates[i];
             track.add(candidates[i]);
             backtrack(candidates,target,i+1);//还是从i+1开始，表示不可复选的  
             sum-=candidates[i];
             track.removeLast();
         }

   for(int i=start;i<candidates.length;i++){
             sum+=candidates[i];
             track.add(candidates[i]);
             backtrack(candidates,target);//表示可复选的，是排序的  
             sum-=candidates[i];
             track.removeLast();
         }

全排列

单词重排

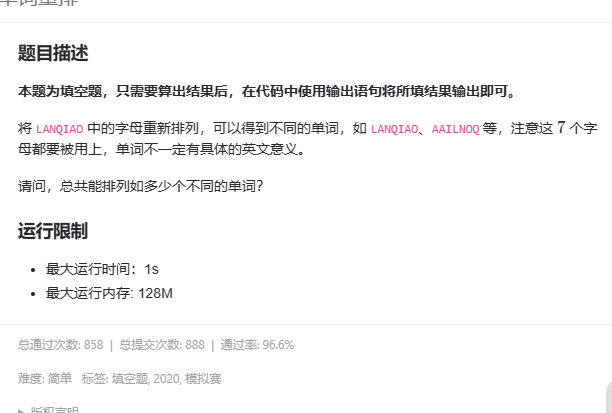
import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

//回溯算法解决排序问题
public class Main {
  static List<List<Character>> res=new LinkedList<>();
        static LinkedList<Character> track=new LinkedList<>();
        static boolean userd[];//定义是否用过
        public static void main(String[] args) {
            String str="LANQIAO";
            paixu(str);
            System.out.println(res.size());
        }
        static  List<List<Character>>  paixu(String str){
            char c[]=str.toCharArray();
            Arrays.sort(c);
            userd=new boolean[str.length()];
            backtrack(c,userd);
            return res;
        }

        static  void backtrack(char c[],boolean us[]){
            if(track.size()==c.length){//达到总长度即退出
                res.add(new LinkedList<>(track));
                return;
            }
            for(int i=0;i<c.length;i++){
                if(userd[i])continue;//当前用过则跳过，因为不重复
              if(i>0&&c[i]==c[i-1]&&!userd[i-1])continue;//相等就跳过，前一个没有用过也跳过
              //进行加入和标记已经使用
                track.add(c[i]);
                userd[i]=true;
                backtrack(c,userd);//继续调用
                //回溯，撤销之前的操作
                track.removeLast();
                userd[i]=false;
            }

        }
}

题目-删除字符

解法一：使用栈

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改


public class Main {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        String str = sc.nextLine();
        char cs[] = str.toCharArray();
        int count = sc.nextInt();
        Stack<Character> stack = new Stack<>();
//L  A   //AN   //ANQ  //AI   //AIA
        for (int i = 0; i < cs.length; i++) {
            while (!stack.isEmpty() && stack.peek() > cs[i]&&count>0) {//元素更大的话
                stack.pop();//弹出去
                if (count--<0){
                    break;
                }
            }
            stack.push(cs[i]);//加入
        }
       StringBuilder sb=new StringBuilder();
        while(!stack.isEmpty()){
            sb.append(stack.pop());
        }
        System.out.println(sb.reverse().toString());

    }
}

解法二：使用集合（原理和栈一致）

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改


public class Main {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        String str=sc.nextLine();
        char chars[]=str.toCharArray();
        int count=sc.nextInt();
        LinkedList<Character> array=new LinkedList<>();
        for (int i=0;i<chars.length;i++){
            //当后一个比前一个更小时，移除前一个，直到，后一个不在小于前一个或者已经达到指定的移除次数
            while(!array.isEmpty()&&chars[i]<chars[i-1]&&count-->0){
                array.removeLast();
            }
            array.add(chars[i]);
        }
        for (Character character : array) {
            System.out.print(character);
        }
    }
}

题目-不同字符的最小子序列

不同字符的最小子序列

 解法一：使用栈

import java.util.Scanner;
import java.util.Stack;

public class 不同字符最小 {
    public static void main(String[] args) {
        Scanner sc =new Scanner(System.in);
        String s = sc.nextLine();
        System.out.println(smallestSubsequence(s));
    }
    public static String smallestSubsequence(String s) {
        Stack<Character> stack=new Stack<>();
        char chars[]=s.toCharArray();
        int count[]=new int[256];
        boolean inStack[]=new boolean[256];
        for (char c:chars){
            count[c]++;//统计每个字符数量
        }
        for (char c:chars){
            count[c]--;//每次遍历都少一个
            if (inStack[c])continue;//已经存在了
           while(!stack.isEmpty()&&stack.peek()>c){
               if (count[stack.peek()]==0)break;//只有一个就不弹出栈了
               inStack[stack.pop()]=false;//标为没有用过
           }
           stack.push(c);
           inStack[c]=true;
        }
        StringBuilder sb=new StringBuilder();
        while(!stack.isEmpty()){
            sb.append(stack.pop());
        }
        return sb.reverse().toString();
    }
}

解法二：使用集合（原理和栈相同）

import java.util.*;

public class 不同字符的最小子序列 {

    public static void main(String[] args) {
       Scanner sc =new Scanner(System.in);
        String s = sc.nextLine();
        System.out.println(smallestSubsequence(s));
    }
    public static  String smallestSubsequence(String s) {
        char chars[]=s.toCharArray();
        int count[]=new int[256];

        for(int i=0;i<chars.length;i++){//统计有这个字符串中的某个字符有多少个
            count[chars[i]]++;
        }
        boolean inChars[]=new boolean[256];
        LinkedList<Character> link=new LinkedList();
        for(int i=0;i<chars.length;i++){
            count[chars[i]]--;
            if (inChars[chars[i]])continue;
            while(!link.isEmpty()&&link.getLast()>chars[i]){//表示前一个元素还有
                if(count[link.getLast()]==0)break;//栈顶元素只存在一个
                inChars[link.removeLast()]=false;//删掉了，改成没添加
            }
            link.add(chars[i]);
            inChars[link.getLast()]=true;//已经添加了
        }
        String res="";
        for(char ss:link){
            res+=ss;
        }
        return res;
    }
}

动态规划

斐波那契数

数组解法-时间复杂度O(n)

    //时间复杂度为O(n)
  static int fib2(int N) {
        int dp[]=new int[N+1];
        dp[1] = dp[2] = 1;
        for (int i = 3; i <= N; i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[N];
    }

 解法二：时间复杂度O(n)

根据斐波那契数列的状态转移方程，当前状态只和之前的两个状态有关，其实并不需要那么长的一个数组来存储所有的状态，只要想办法存储之前的两个状态就行了。

  //时间复杂度为O(1)
   static int fib(int n) {
        if (n < 2) return n;
        int prev = 0, curr = 1;
        for (int i = 0; i < n - 1; i++) {
            int sum = prev + curr;
            prev = curr;
            curr = sum;
        }
        return curr;
    }

对比一下两者所消耗时间

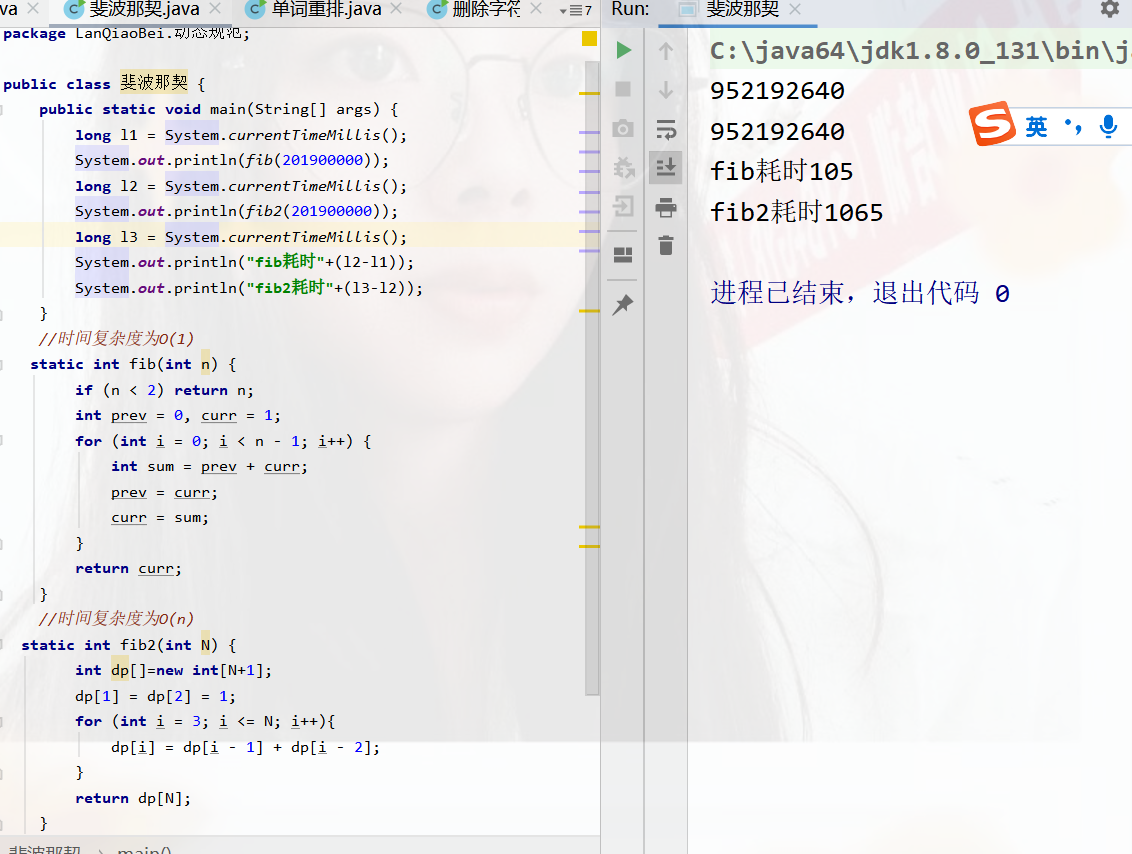
题目-零钱兑换

零钱兑换

法一：带备忘录的递归 

package LanQiaoBei.动态规划;


import java.util.Arrays;

public class 零钱兑换 {
    public static void main(String[] args) {
        int coins[]={1,3,5};
        int amount=11;
        System.out.println(coinChange(coins, amount));
    }
    //备忘录
    static int memory[];
    public static int coinChange(int coins[],int amount){
        memory=new int[amount+1];
        Arrays.fill(memory, -66);//初始化
        return dp(coins, amount);
    }
    public static int dp(int coins[],int amount){
        if (amount==0)return 0;
        if (amount<0)return -1;
        //查询备忘录，防止重复
        if (memory[amount]!=-66)return memory[amount];//已经查过
        int res=Integer.MAX_VALUE;
        for (int coin:coins){
            //计算子问题结果
            int subPro = dp(coins, amount - coin);
            if (subPro==-1)continue;//跳过，说明这个不通
            res=Math.min(res, subPro+1);//在子问题求得最优解后，每次加一
        }
       memory[amount]=res==Integer.MAX_VALUE?-1:res;//等于最大值说明一直被跳过
        return memory[amount];
    }
}

法二：dp 数组的迭代解法

int coinChange(int[] coins, int amount) {
    int[] dp = new int[amount + 1];
    // 数组大小为 amount + 1，初始值也为 amount + 1
    Arrays.fill(dp, amount + 1);

    // base case
    dp[0] = 0;
    // 外层 for 循环在遍历所有状态的所有取值
    for (int i = 0; i < dp.length; i++) {
        // 内层 for 循环在求所有选择的最小值
        for (int coin : coins) {
            // 子问题无解，跳过
            if (i - coin < 0) {
                continue;
            }
            dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
        }
    }
    return (dp[amount] == amount + 1) ? -1 : dp[amount];

位运算操作

运用异或运算的性质：

一个数和它本身做异或运算结果为 0，即 a ^ a = 0；一个数和 0 做异或运算的结果为它本身，即 a ^ 0 = a。

一个数异或n个数的和顺序无关

查找只出现一次的元素

int singleNumber(int []nums) {
    int res = 0;
    for (int n : nums) {
        res ^= n;
    }
    return res;
}

最小公约数、公倍数

    //返回值则是a和b的最大公约数
   static int gcd(int a,int b){
        return b == 0 ? a:gcd(b,a%b);
    }
    //返回值为a和b的最小公倍数
   static int lcm(int a, int b){
        return a*b/gcd(a,b);//最小公倍数=两数之积÷两数最大公约数
    }

二分查找

https://leetcode.cn/problems/first-bad-version/

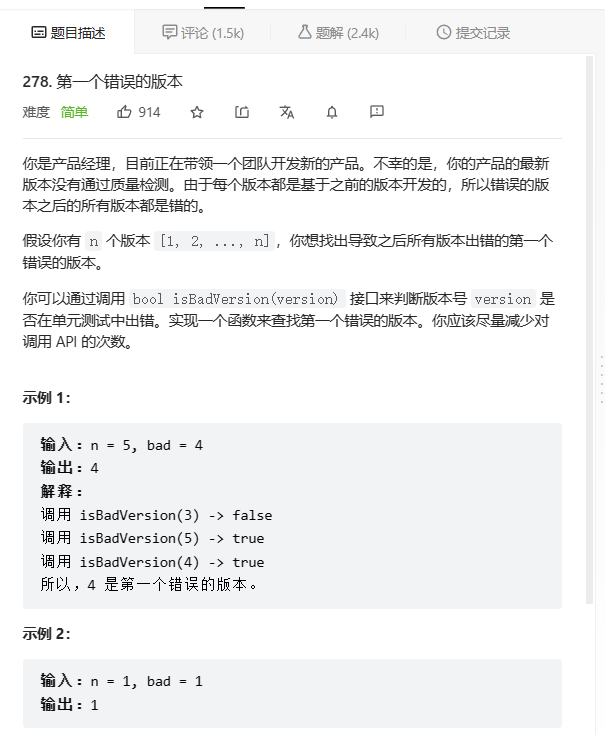
public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int left = 1, right = n;
        while (left < right) { // 循环直至区间左右端点相同
            int mid = left + (right - left) / 2; // 防止计算时溢出
            if (isBadVersion(mid)) {
                right = mid; // 答案在区间 [left, mid] 中
            } else {
                left = mid + 1; // 答案在区间 [mid+1, right] 中
            }
        }
        // 此时有 left == right，区间缩为一个点，即为答案
        return left;
    }
}

高效求素数

不用从i<n开始，可以从i*i<n开始，因为之后的都是对称的

一个数只要是素数的整数倍那他不是素数。

int countPrimes(int n) {
    boolean[] isPrime = new boolean[n];
    // 将数组都初始化为 true
    Arrays.fill(isPrime, true);

    for (int i = 2; i < n; i++) 
        if (isPrime[i]) 
            // i 的倍数不可能是素数了
            for (int j = 2 * i; j < n; j += i) 
                    isPrime[j] = false;
    
    int count = 0;
    for (int i = 2; i < n; i++)
        if (isPrime[i]) count++;
    
    return count;
}

法二： 

class Solution {
    public int countPrimes(int n) {
        boolean[] isPrime = new boolean[n];
        Arrays.fill(isPrime, true);
        for (int i = 2; i * i < n; i++) 
            if (isPrime[i]) 
                for (int j = i * i; j < n; j += i) 
                    isPrime[j] = false;
        
        int count = 0;
        for (int i = 2; i < n; i++)
            if (isPrime[i]) count++;
        
        return count;
    }
}

 题目：买不到的数

对于互质的两个数a和b，其不能组成的最大整数为a*b-a-b。

正则匹配

public class 正则 {
    public static void main(String[] args) {
        // $0 表示匹配到的第一个字符（即该大写字母）
        // _$0 表示在匹配到的大写字母前加一个下划线（作为分隔符使用）
        String str="LanTaiXiaoQiao";
        String temp = str.replaceAll("[A-Z]", "_$0");
        System.out.println(temp);
        String[] split = temp.split("_");

    }
}