文章目录
- 前言
- Lecture5 Real-time Environment Mapping (prefiltering,split sum)
- 补充:反射波瓣(Lobe)
- Lecture6 Real-time Environment Mapping (precomputed radiance transfer)
- Spherical Harmonics
- precomputed radiance transfer
- DIffuse 的情况
- Glossy 的情况
- 总结
- 存在的问题:
- 更进一步的研究:
前言
课程录播:
https://www.bilibili.com/video/BV1YK4y1T7yY?p=5
课程主页:
https://sites.cs.ucsb.edu/~lingqi/teaching/games202.html
课程BBS:
http://games-cn.org/forums/forum/games202/
Lecture5 Real-time Environment Mapping (prefiltering,split sum)
环境光照:用一张图来记录在场景中往任何一个方向看,可以看到的方向。
隐含条件:环境光照来自无穷远处。
给了一个环境贴图,如何求一个点的shading呢?自然是回归我们的渲染方程:

我们注意到,如果 BRDF 是glossy的(BRDF是 出射光的 Ridiance 的微分 比上 入射光的 Irradiance 的微分),此时集中在一小块区域,积分域 support 是很小的;如果 BRDF 是 diffuse 的,那他是比较平滑smooth的。
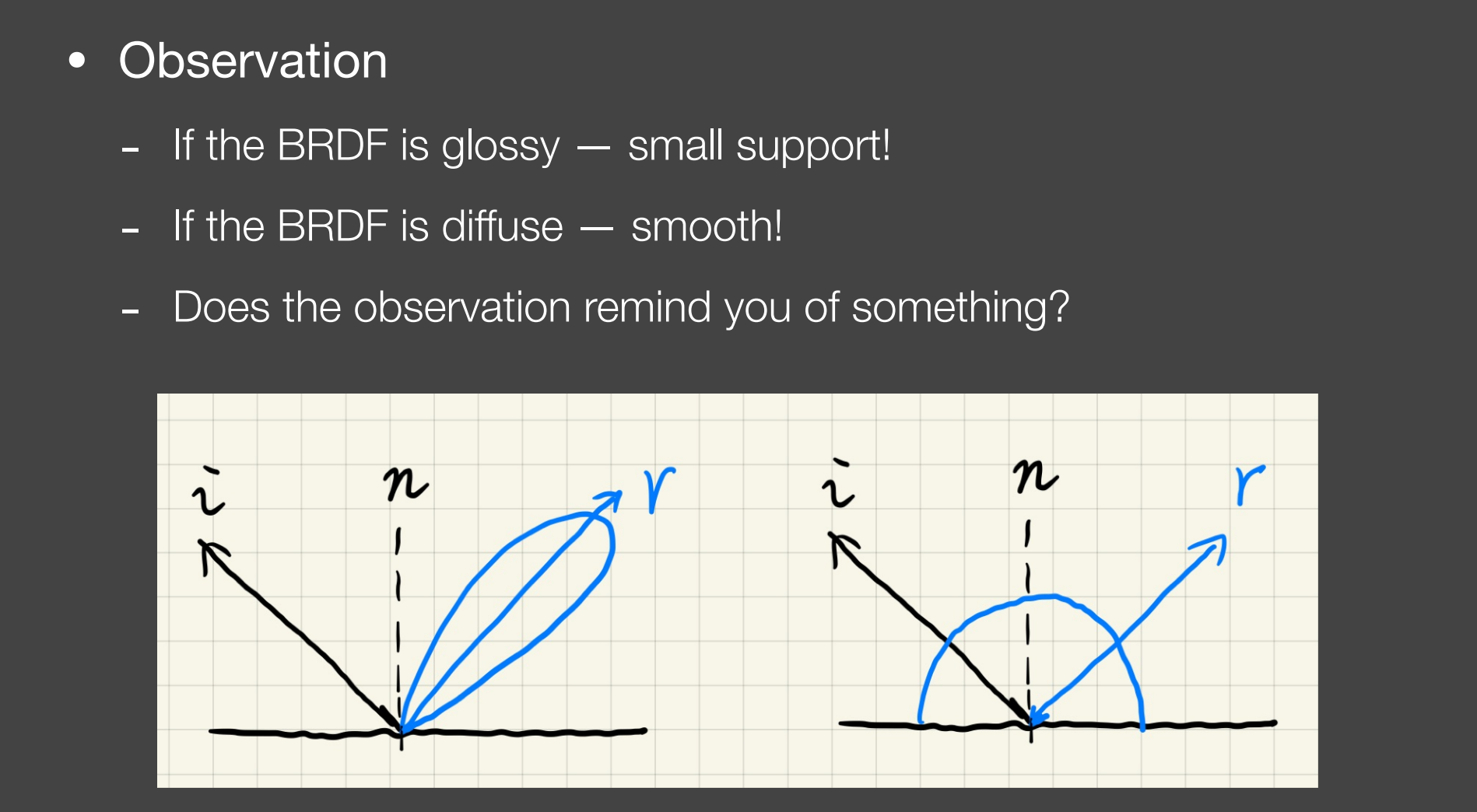
这就联想到之前讲阴影的时候,我们说那个近似公式的成立条件了:

于是我们可以先把 BRDF 从渲染方程里抽出来:

这样拆除来的好处是:light 和 brdf 一起作用我们不好求,我们这样可以把 brdf 表示的某个区域给积分起来再平均化,其实就是把 IBL 所表示的图给模糊了:

也就是我们可以去滤波我们的环境光,这个滤波核取多大取决于我们的 BRDF 占多大。
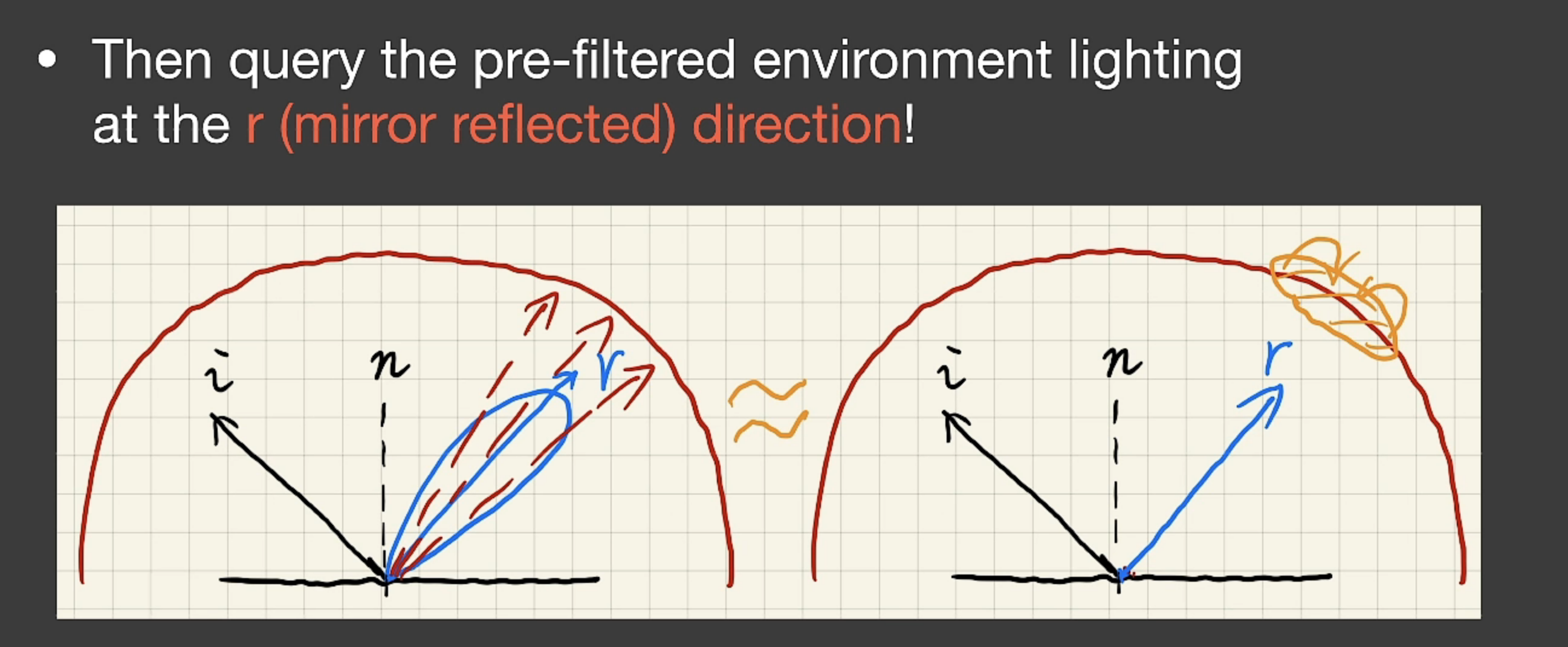
补充:反射波瓣(Lobe)
参考文章:
https://zhuanlan.zhihu.com/p/144437629
发现闫老师常用 lobe ,比如:
其实就是用反射波瓣去表示 BRDF,也即反射的分布。波瓣小,表示反射后的分布较集中(可以理解成分布在这个波瓣lobe上?),这个shading point比较glossy;反之,波瓣大,则diffuse
继续说,如上图左侧,我们查询反射的值,只能在球面上查对应反射方向的那一个值,这样就无法体现我们的 lobe;但没关系,我们提前做好了 filter,那么查询就是已经滤波后的值,也就相当于查询了周围一片方向的值(即这个 lobe 范围的值),如上图右侧。
举个例子,比如环境贴图是2k的,然后做了一个 filter 卷积模糊到了一个新的图;我们想查询一个 lobe 打过去的值,需要在原图找到这个 lobe 打中的那一块区域;但这里我们直接在原图上做了一个卷积模糊,新的图的一个像素就包含了周围像素的信息,因此只考虑 lobe 中心那个方向打中的地方也包含了之前整个 lobe 的信息(这时候涉及到 lobe 的大小我们就需要用插值了,双线性、三线性…)
回归原来的方程,我们还剩下对剩下的部分的积分:

如果要做预计算,角度一维、rgb三维、Roughness一维,一共五维的查找表,要存一个五维纹理,存储势必会爆炸(一般存三维纹理都很难接受了),因此不能硬存。
回顾:Microfacet BRDF
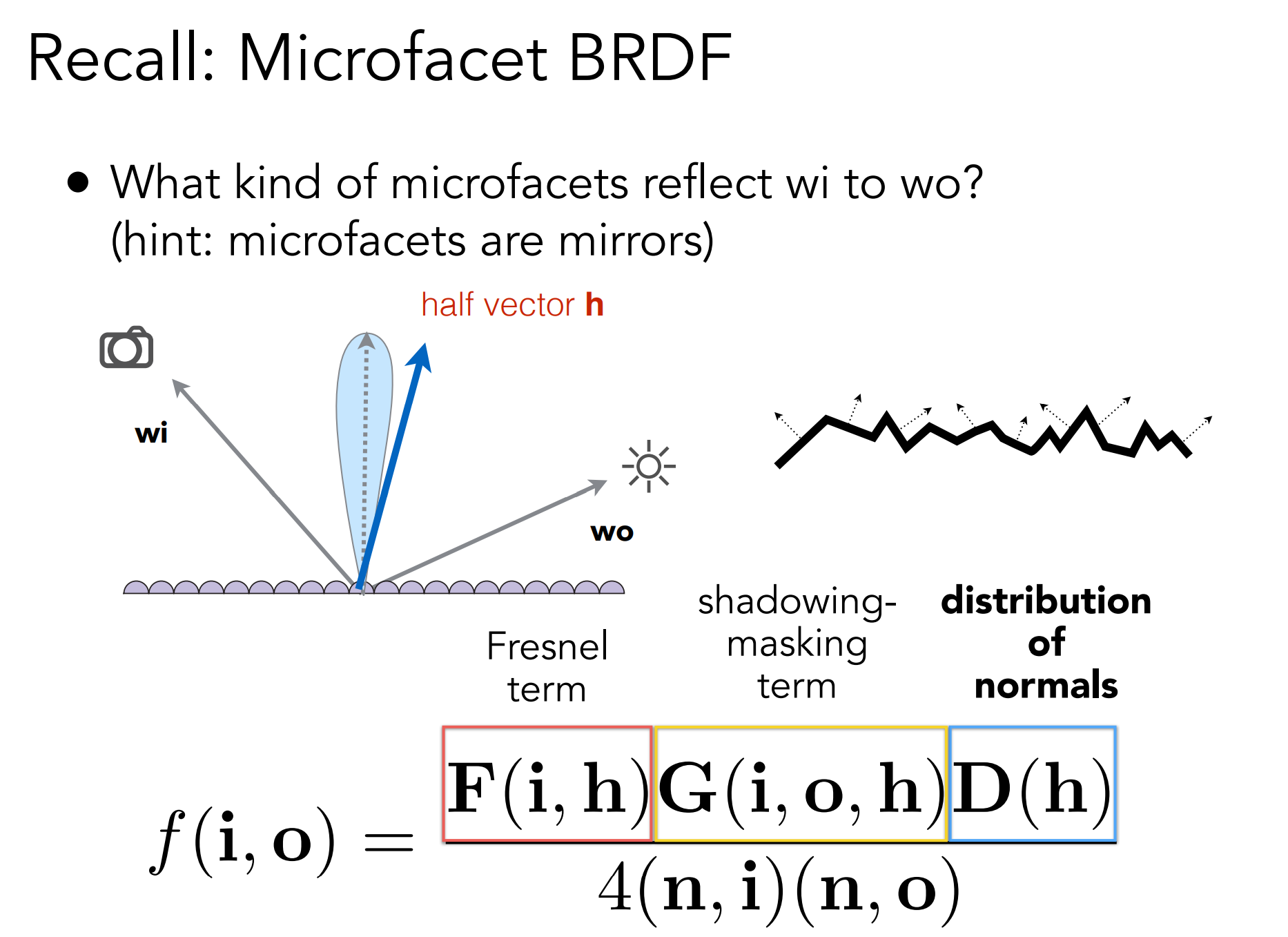
Fresnel 项可以用 Schlick 近似,NDF(法线分布函数,Normal Distribution Function) 也可以用一些分布去近似:

回顾旧笔记:https://zhuanlan.zhihu.com/p/427854383
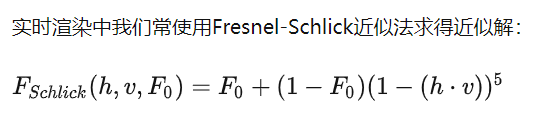
这里我们把 F0 提出来(在202里面叫做R0),可以把原来的BRDF变成这样(除以一个菲涅尔项再乘以一个,乘以的那一个用Schlick近似):

这样做的好处是可以把 R0 拆到积分外面去,而 R0 是事先给好的,可以看作一个常数。
注:见我前面的笔记链接:
R0 就是上面的 F0 即 基础反射率,这是三维的,我们这样拆其实就是把这三维给剥离出积分项,而可以事先就给定这三维的指(其实也就和这个物体表面的颜色值相关了,PBR流程中查一个albedo贴图即可),因此从原先的五维降到了二维,从而可以预先计算出纹理来查找。
而剩下的几项又其实只和 Roughness 以及 Cos 项相关,于是可以预积分成一张纹理:

因此对于上面右边的那个式子,拆出来的两个积分项都只和 theta 以及 Roughness 相关,我们可以预先计算出来,并分别存入纹理的 R 和 G 通道即可,也因此上图的那个纹理是红绿色的(有这两个通道的值)。
Lecture6 Real-time Environment Mapping (precomputed radiance transfer)
实时渲染从环境光计算出阴影,非常非常难。high level 下来讲就是做不到。
但是也有一个工业界的解决方案,就是只生成一个最亮的光源下的阴影(比如太阳光)。另外一个就是PRT(precomputed radiance transfer)。
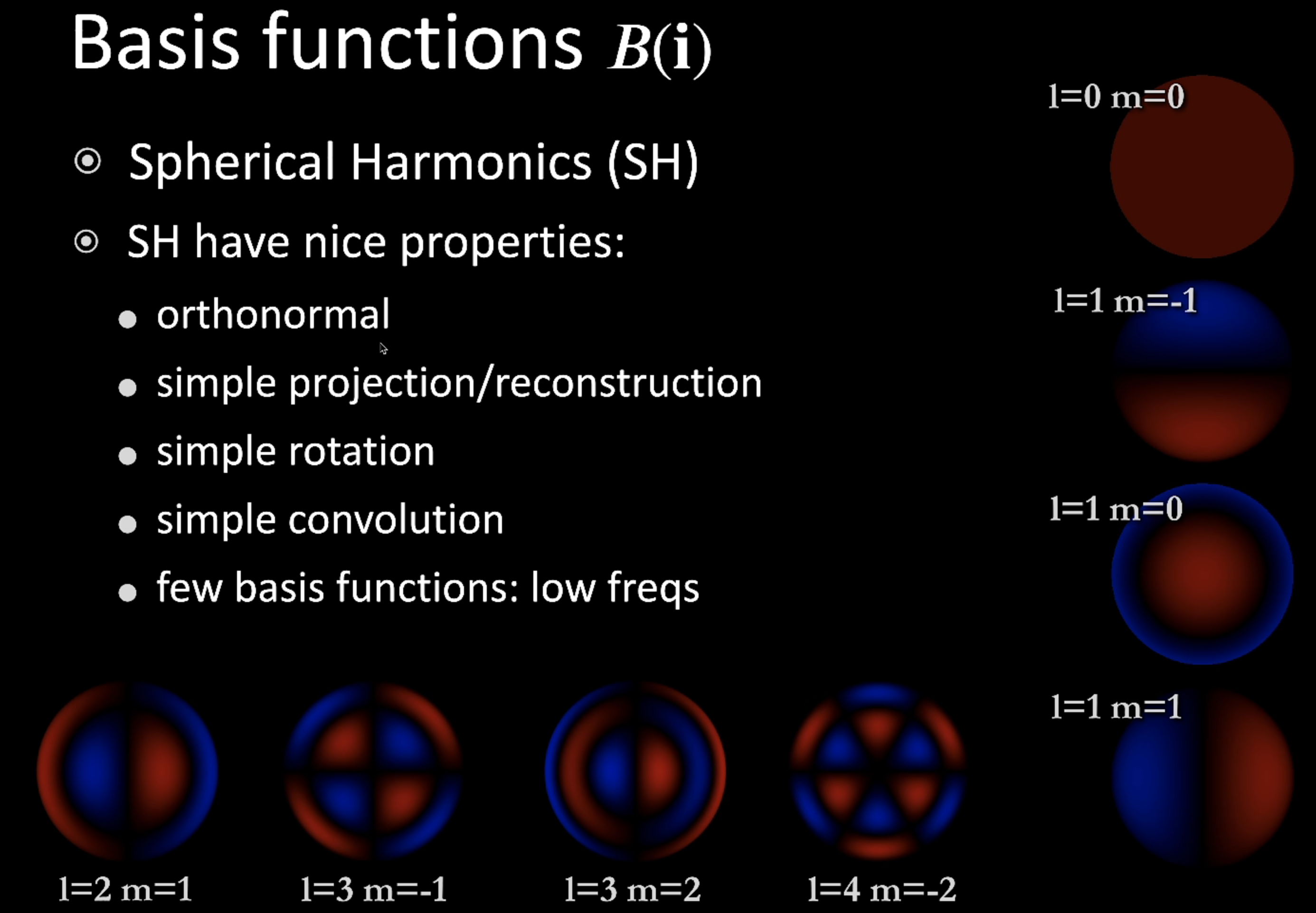
Spherical Harmonics
他是一系列的二维基函数,并且定义在球面上的(三维空间中的一个方向是二维的,因为可以拿 theta 和 phi 来描述)。有点像在一维情况下的傅里叶函数。

如上图,球谐函数每一行所描述的频率都是一样的,只是旋转或者形状有所不同。(颜色表示值大小,蓝色中越白的表示值越大,黄色则为负的,越白则绝对值越大。这里仅仅是可视化)
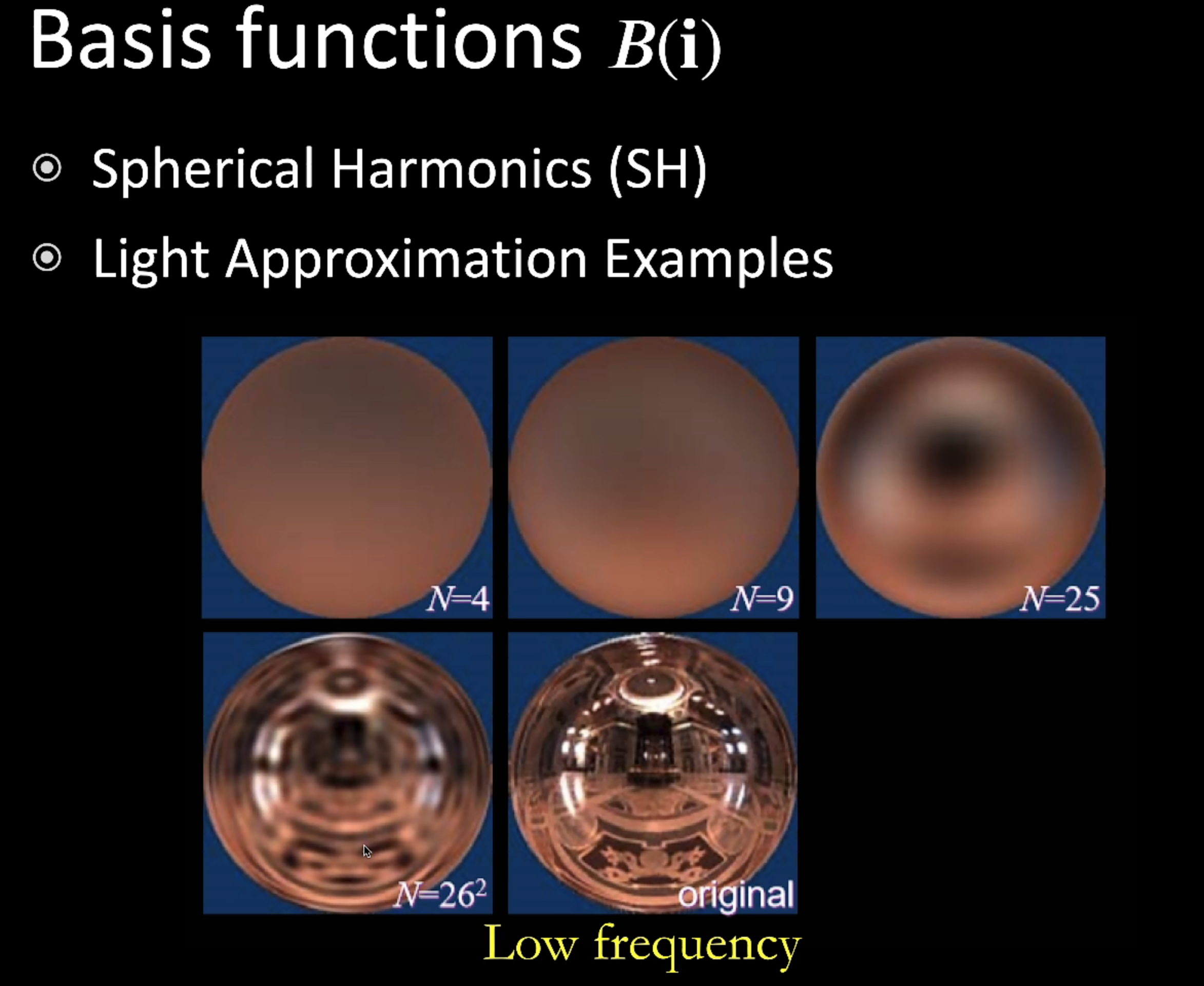
因此 Spherical Harmonics 仅仅是一系列二维的函数,并且他们有着不同的频率。并且每一行函数的个数就是 2 l + 1 个。l = k 叫做第 k 阶的SH,编号从 -k 到 k。(每一阶描述一个频率,阶越高频率越高)。每一个阶函数在数学上可以用勒让德多项式去描述。
给一个球面函数,用任意一组基底(记为Bi),前面的系数(记为Ci)可以很快求出来:

求这个系数的过程就叫做投影。
可以额外参考:
https://zhuanlan.zhihu.com/p/359856625
不过我们要是想恢复这个函数,我们其实不需要用到那么多阶(即不需要那么精确)。比如可以用前四阶的SH来恢复原来的函数,那么恢复出来的函数保留的最高的频率就是 l = 3 的频率,更高的被我们给扔了。这意味着我们只是损失了一些细节(高频),大体还是准的。(一般用前多少阶,则这些阶的基函数通常我们都用,比如 l = 2 第二阶,这五个基函数我们都用)
于是SH可以用来近似光照,比如之前说的某一点求shading的时候求他的球面的 irradiance 值。并且在 Diffuse 的 BRDF 下,本身的 shading 就主要是低频的信息,只需要用到前三阶(l = 012)的 SH 就可以描述了。
于是只剩下两个问题了:shadow 以及 非diffuse的BRDF
precomputed radiance transfer

这里BRDF是一个四维的,代表入射角和观察角,球面坐标一个方向是二维。这里是对某一个特定的shading point、特定的观察点来求BRDF值,那么观察方向已知,我们就可以对不同的入射方向存成一个贴图了,就像图中的BRDF那个黑白图一样。
注:
个人理解:
出射角的radiance微分比上入射角的irradiance微分,因为 radiance 的测量和光源大小相关,所以入射用irradiance,直接弄一个面积就可以方便测量了,单位是 sr-1,也就是球面度分之1,因为radiance比irradiance多除以了一个单位立体角(单位即球面度)。
而之所以微分的比可以作为一个值存在贴图中,是因为我们默认应该都是单位大小的。就像功率是一样,Q是焦耳,t是秒,功率是瓦特,也就是一个单位时间内通过表面或者空间区域的能量的总量,因此这个积分应该默认是0到1的。
但是这只是一个shading point的计算,每次算三个值的乘积,一张图那么多分辨率,要全算一遍积分,这也太费了。于是搞出个PRT
DIffuse 的情况

我们做出假设:渲染的时候只有光照可以发生变化(例如换一种光照或者光照旋转),场景其他东西不变。那么我们就可以把渲染方程看成 lighting 和 light transport 两部分。
这样假设之后,light transport 其实只是针对一个点shading point的性质,于是可以提前预计算出来。并且在其他场景都不变的情况下 light transport 其实也就是一个球面函数(观察方向为两维自变量)。
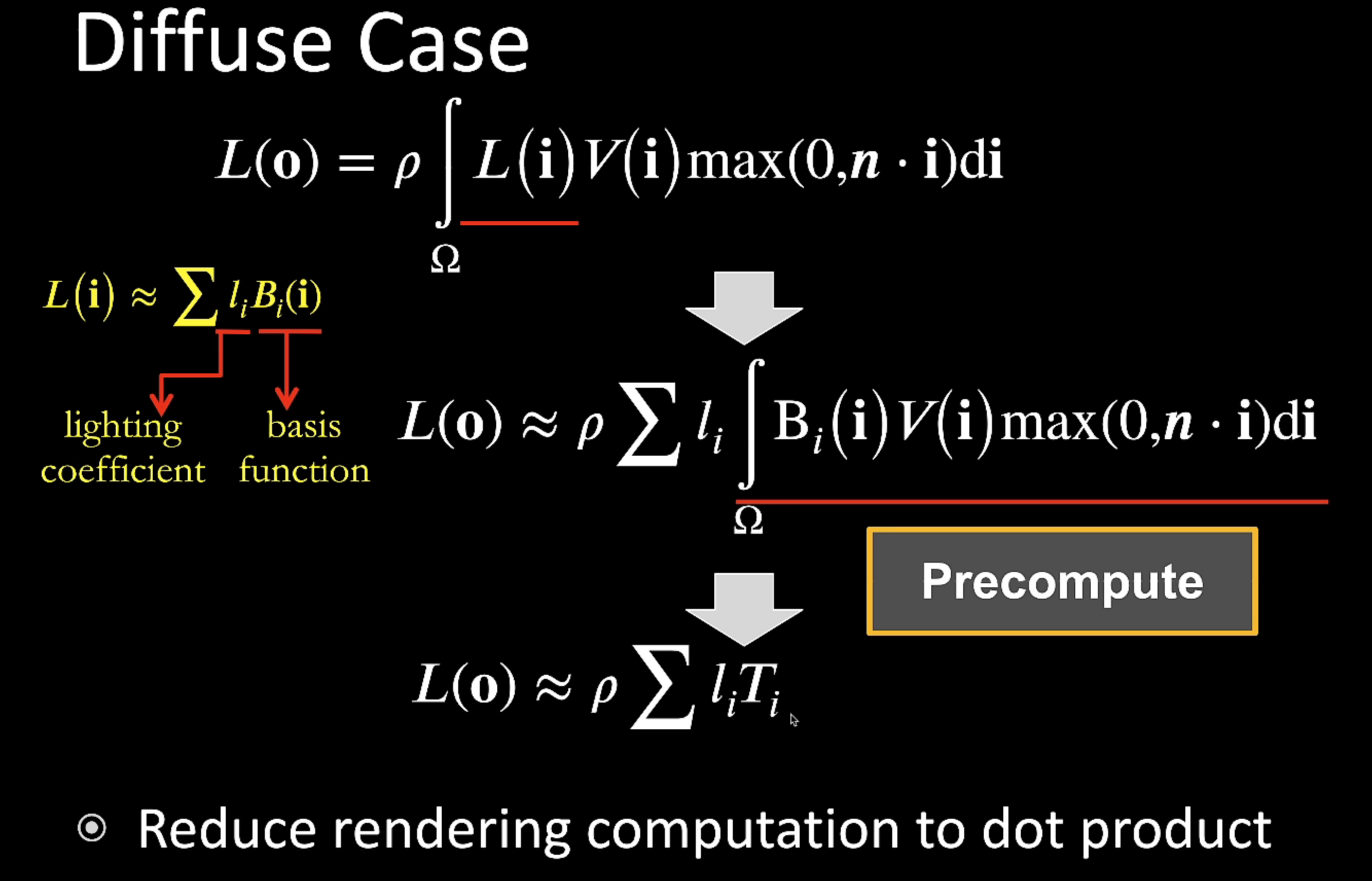
我们把Light球谐展开,并且把BRDF提出来(diffuse情况下),做可以交换的假设,如上。剩下的 light transport 乘上那个球谐系数的积分 其实也就是 整个函数在这组球谐基上的投影。这部分的积分是可以预计算出来的。
但是代价是 light transport 所有东西都是固定的,这就意味着 visibility 项也是固定的,也就意味着场景所有的东西都是不能动的。另外一个代价是 Light 也做了预计算,那么只要光源被预计算过就可以替换,但是光源要是一旋转也就相当于换了一种光源,然而球谐具有旋转不变性,因此其实这种情况是可以处理的。( visibility 项是从 shading point 朝四面八方看,那个方向是否会被物体挡住,和光源没关系,我认为更确切的说是和环境光没关系)
因此之前说旋转光源,其实跟旋转球谐系数是一样的,我们就相当于把旋转光源变成了旋转任意一个 SH Basis。但是球谐的一个好性质是,旋转任意一个SH Basis他都能被同阶的 SH 的线性组合所得到。
因此,我们得出:要是光源旋转了,相当于对 SH 旋转,每一阶的 SH 旋转后都能被同阶的 SH 的线性组合所得到,于是又产生了新的一组 SH 系数,因此我们可以预先算出系数,得到一张表就行了。

Glossy 的情况
Glossy 和视点有关,BRDF 是四维的。因此 Light Transport 在 i 的方向的 SH 投影出来一定是一个关于 o (观察方向)的函数。
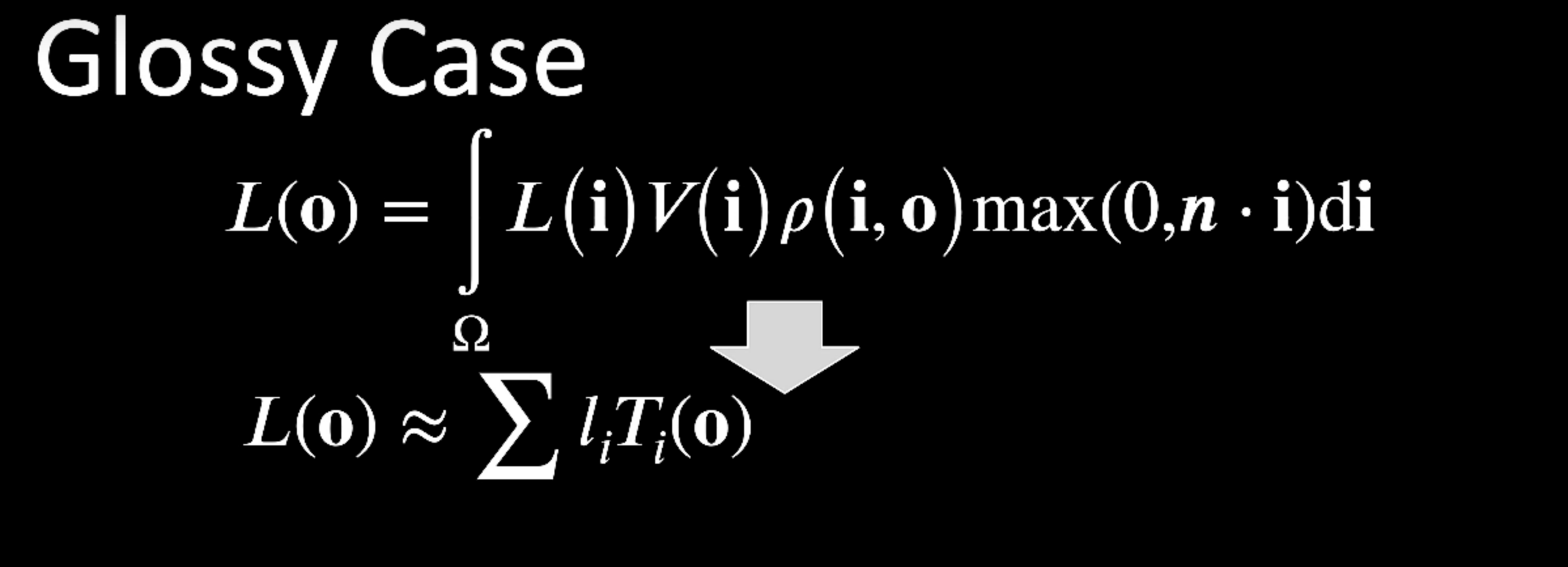
那么人们就想到也可以在 o 的方向投影出来一个 SH 结果:
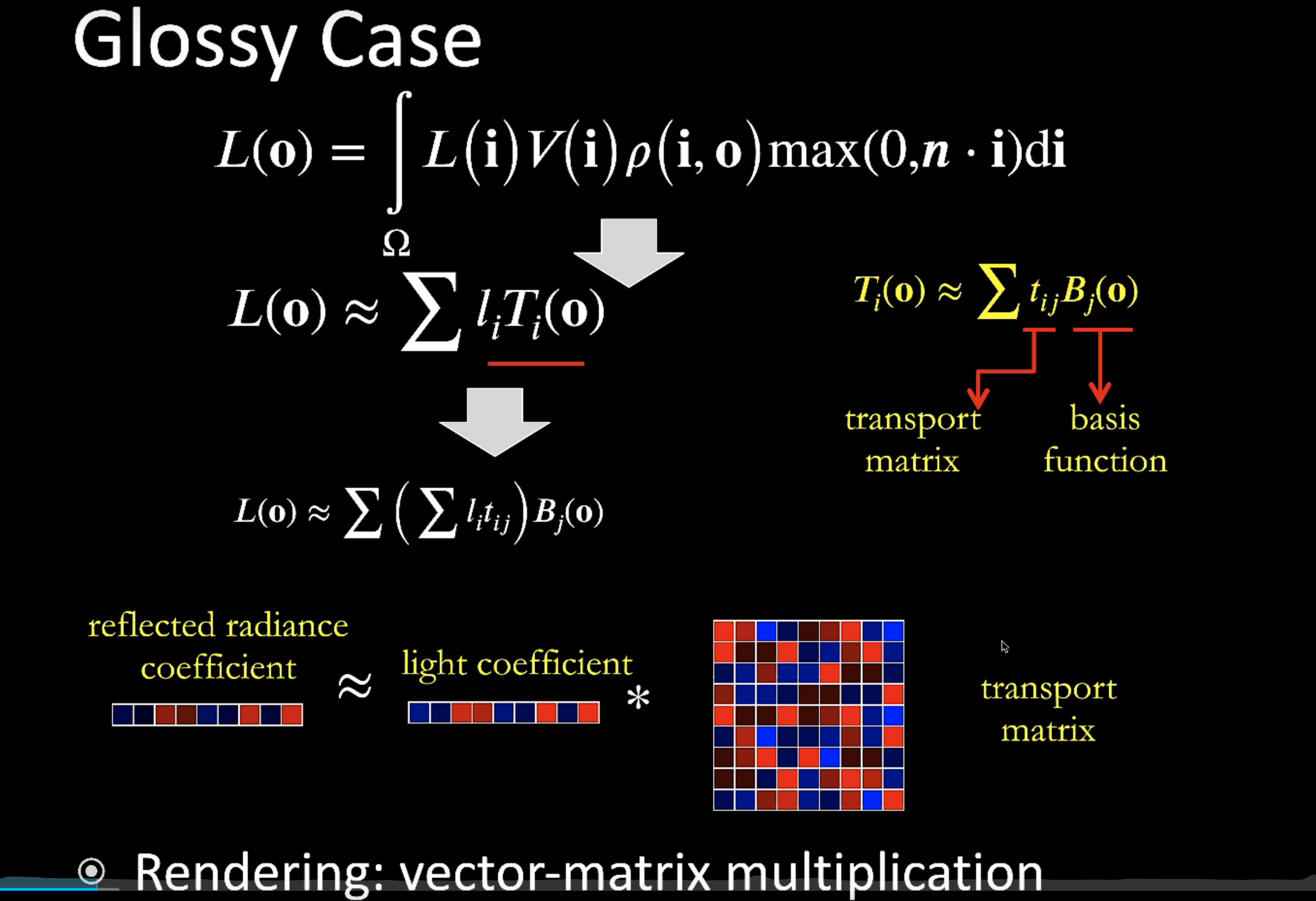
因此其实就是对 diffuse 情况的一组延申:对任何一个 shading point 都需要存他的 transport matrix。

科研领域 glossy 的物体大家觉得十阶 SH 都还不够呢。当 glossy 非常高频的情况下,SH描述的效果并不好。(diffuse、glossy、specular,一般 glossy 介于 diffuse 和 specular 中间,不太严格的话可以认为glossy和specular差不多)
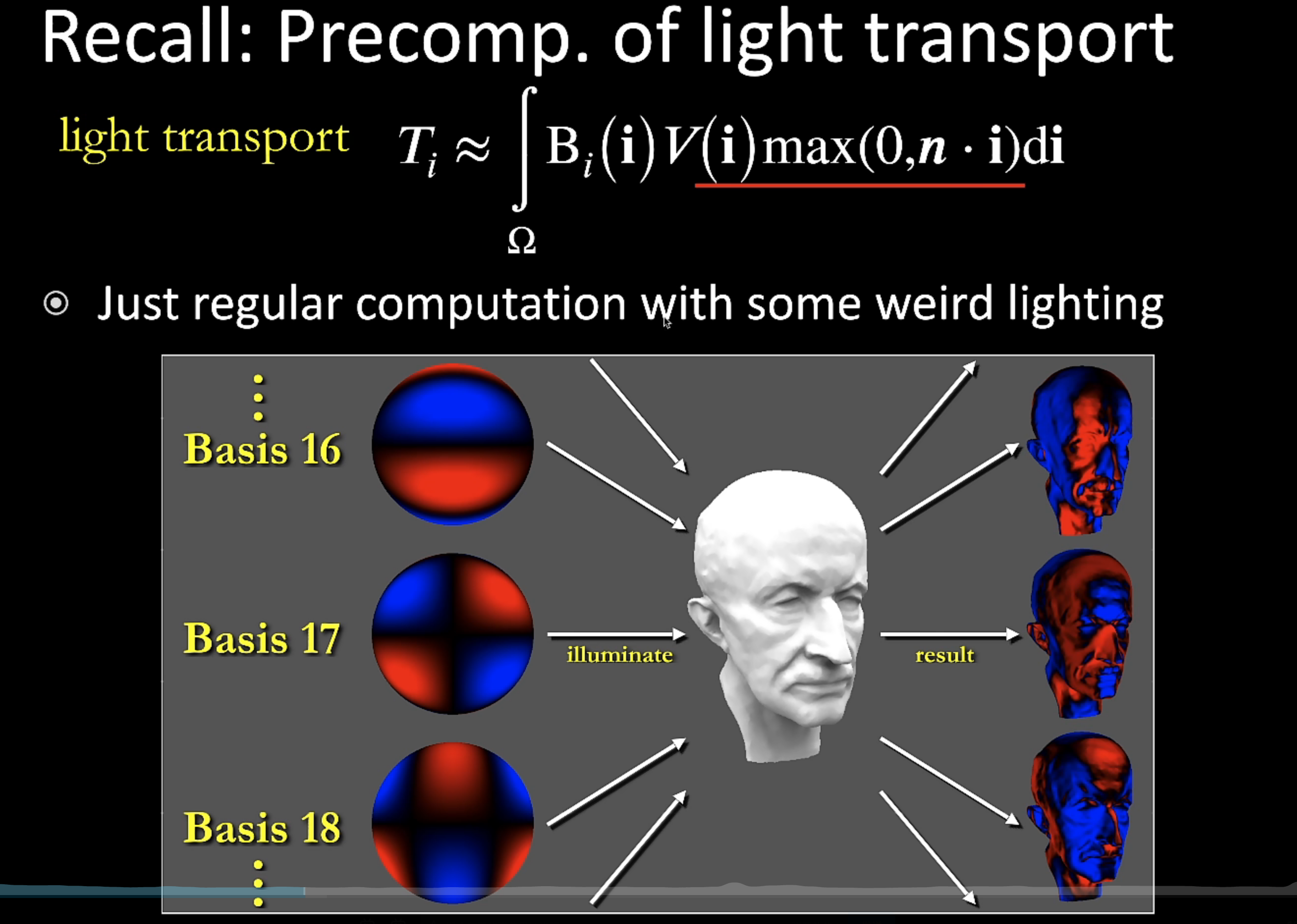
我们之前的 light transport 投影到 SH 上面去的这个式子(上图),还可以理解成,把每个 SH 的基函数看作一种光源,上式看成 rendering equation,然后就是这个光照来照亮了每个顶点,并且把这个照亮结果给记录下来。(上图是可视化了,红的越厉害表示越正,蓝的越厉害表示越负,所以看着有些奇怪)

像上图这种 Spatially Varying,即一个物体上任意一点也可能是另一种 BRDF,那么整个物体的 BRDF 就上升到六维了(物体上不同点的位置占二维)
总结
总结一下最早的这篇 PRT,它首先描述了用 SH 来把描述 lighting 和 light transport 两部分,对于 diffuse 的情况下就可以在每个 shading point 做一个点乘的操作,而如果是 glossy 的情况下每个顶点就做一个向量乘以矩阵的一个操作。

存在的问题:
- SH 基本上只适合描述低频的函数,比如下图用了 26 阶才基本恢复出高频来。
- 做了一个假设,一旦要预计算就需要场景是固定住的,即只适用于静态场景。场景中就不能动态去改变它的材质。
- 需要大量的预计算数据,带来存储以及读取的开销。

更进一步的研究:
PRT 一些其他思路:
不用SH换成别的基函数、不用点积等等。