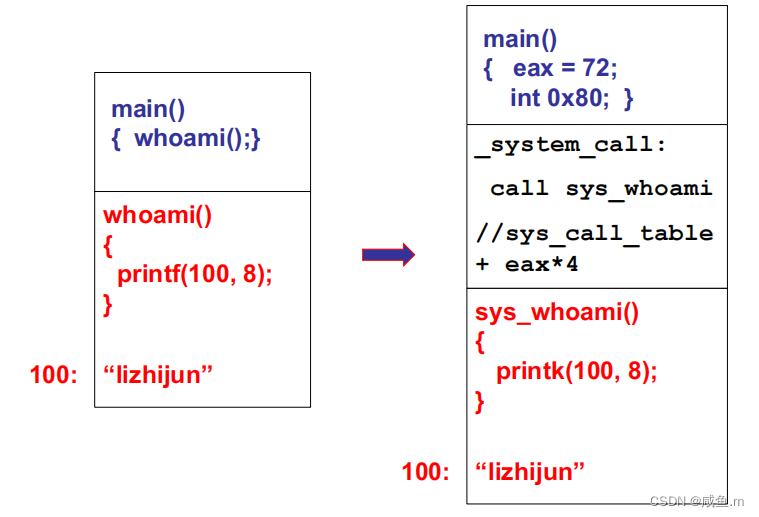
题目

n*n的网格(n<=2e3)，

每个网格内的字符是O或者X，其中O表示(i,j)上有一个棋子，X表示没有

位于(s,t)棋子覆盖住了方格(u,v)，当且仅当：

1.

2.

3.

q(q<=2e5)次询问，第i次给出一个方格位置(xi,yi)(1<=xi,yi<=n)，

询问有多少棋子覆盖住了这个方格

思路来源

官方题解&aging佬代码

题解1

Editorial - AtCoder Beginner Contest 260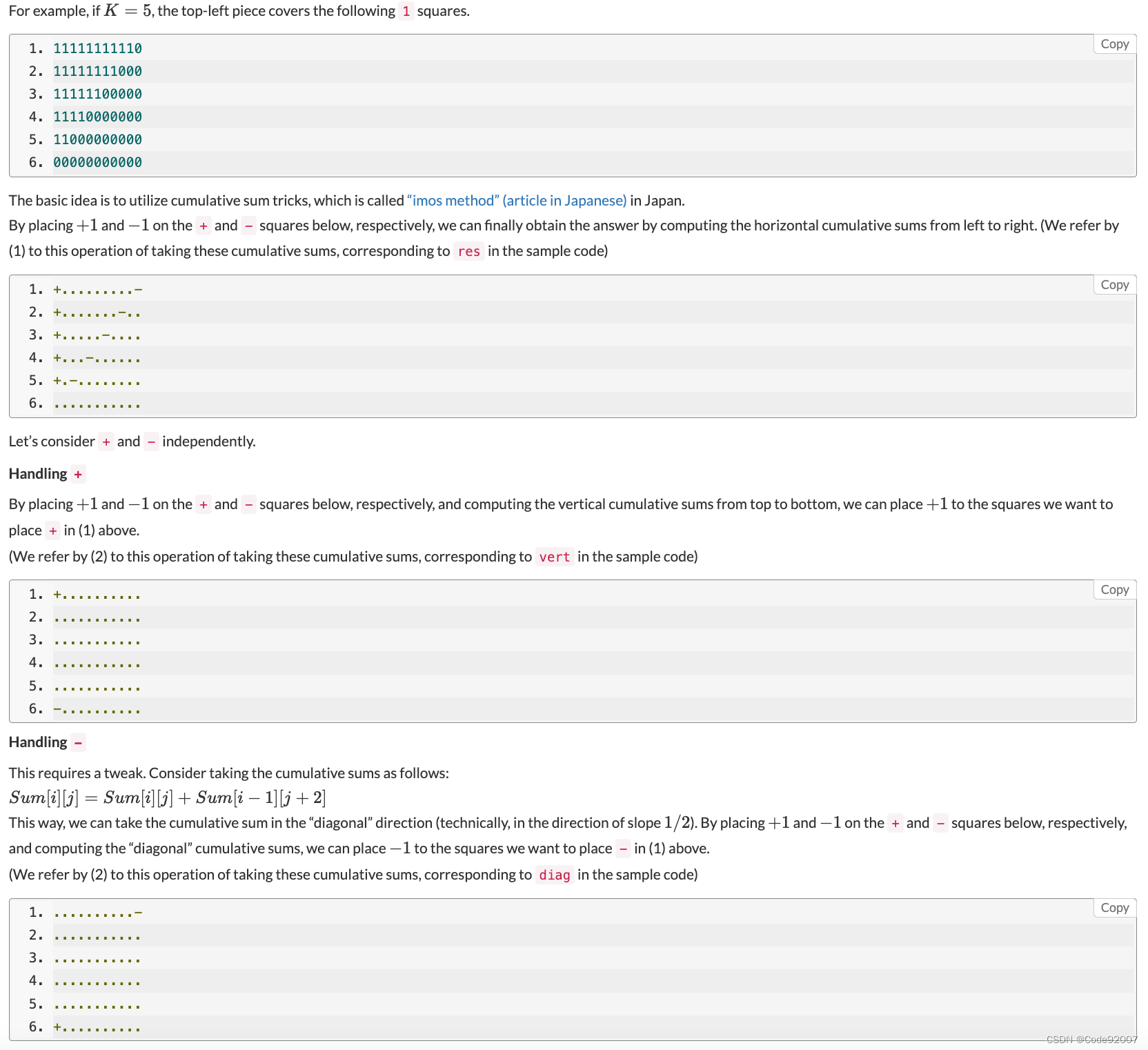

 可以发现，+1的区域形似一个三角形，纵向失效处为u-s=m，横向失效处为(v-t)/2=m

横向一维差分后得到第二个图，考虑将+和-分开处理，再差分一次，

于是，+是一个列方向差分，-是一个(+1,-2)方向的差分，

如图三和图四所示，分两个数组维护这两部分的二维差分数组，

分别按列/按(1,-2)方向，求得一维差分数组，

再按行求一遍前缀和，即得到原数组

题解2

将第三个式子化简，有2u+v<2s+t+2*m，相当于有三维权值

即对于每个点(u,v,w)来说，只统计s<=u且t<=v且w>2u+v的点(u,v,w)

而对于棋子(u,v,w)来说，其权值w=2*u+v+2*m

类似一个三维数点问题，控制i这一维本身自增，

剩下的开二维线段树来维护，这里二维树状数组常数相对小一些

代码1（二维差分）

#include<iostream>
#include<cstdio>
using namespace std;
const int N=2e3+10,M=2*N,K=1e4+10;
int n,m,q,x,y,ver[N][K],diag[N][K],ans[N][K];
char s[N];
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;++i){
        scanf("%s",s);
        for(int j=0;j<n;++j){
            if(s[j]=='O'){
                ver[i][j]++;
                if(i+m<N)ver[i+m][j]--;
                diag[i][j+2*m]--;
                if(i+m<N)diag[i+m][j]++;
            }
        }
    }
    for(int i=1;i<N;++i){// 竖向前缀和 斜向前缀和
        for(int j=0;j<K;++j){
            ver[i][j]+=ver[i-1][j];
            if(j+2<K)diag[i][j]+=diag[i-1][j+2];
        }
    }
    for(int i=0;i<N;++i){
        for(int j=0;j<K;++j){
            ans[i][j]=ver[i][j]+diag[i][j];
        }
    }
    for(int i=0;i<N;++i){// 横向前缀和
        for(int j=1;j<K;++j){
            ans[i][j]+=ans[i][j-1];
        }
    }
    scanf("%d",&q);
    while(q--){
        scanf("%d%d",&x,&y);x--;y--;
        printf("%d\n",ans[x][y]);
    }
    return 0;
}

代码2（二维树状数组）

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
//2*u+v<2*M+2*s+t
const int N=2e3+10,M=2*N,K=2*M+3*N;
int n,m,q,x,y,res[N][N];
char s[N][N];
struct BIT{
	int n,m,tr[N][K];
	void init(int _n,int _m){
		n=_n;m=_m;
		memset(tr,0,sizeof tr);
	}
	void add(int x,int y,int v){
		for(int i=x;i<=n;i+=i&-i){
            for(int j=y;j<=m;j+=j&-j){
                tr[i][j]+=v;
            }
        }
	}
	int sum(int x,int y){
		int ans=0; 
		for(int i=x;i;i-=i&-i){
            for(int j=y;j;j-=j&-j){
                ans+=tr[i][j];
            }
        }
		return ans;
	}
}tr;
int main(){
    scanf("%d%d",&n,&m);
    tr.init(n,2*m+3*n);
    for(int i=1;i<=n;++i){
        scanf("%s",s[i]+1);
        for(int j=1;j<=n;++j){
            if(s[i][j]=='O'){
                tr.add(j,2*m+2*i+j,1);
            }
            //printf("i:%d j:%d sum2:%d sum:%d\n",i,j,tr.sum(j,2*m+3*n),tr.sum(j,2*i+j));
            res[i][j]=tr.sum(j,2*m+3*n)-tr.sum(j,2*i+j);
        }
    }
    scanf("%d",&q);
    while(q--){
        scanf("%d%d",&x,&y);
        printf("%d\n",res[x][y]);
    }
    return 0;
}