前言
A* 寻路算法是什么
游戏开发中往往有这样的需求,让玩家控制的角色自动寻路到目标地点,或是让 AI 角色移动到目标位置,实际的情况可能很复杂,比如地图上有无法通过的障碍或者需要付出代价(时间或其他资源)才能通过的河流、沼泽等,想要让角色找到一条付出最小代价到达目标的路径,就需要使用一些特殊的算法,而 A* 寻路算法就是目前应用最广泛的寻路算法之一,unity asset store 上广受好评的 A* Pathfinding project 插件也是基于 A* 寻路算法实现的,简单来说:A* 算法是一种寻找最短路径并避开障碍物的算法。
A* 算法的基本概念
至于为何A* 是寻路最受欢迎的选择,是因为它非常灵活,可以在各种环境中使用。
像 Dijkstra 算法一样,它可以用来找到最短的路径。
像贪心算法一样,它可以使用启发式来指导自己。在简单的情况下,它与贪心算法一样快:

在具有凹陷障碍物的示例中,A* 可以找到与Dijkstra算法找到的路径一样好的路径:
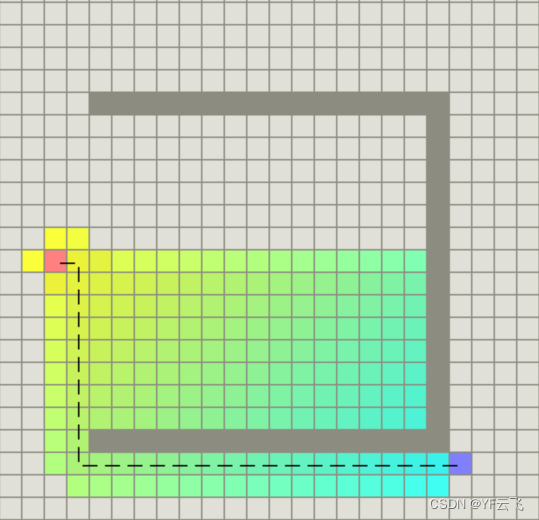
它成功的秘诀在于它结合了Dijkstra算法使用的信息(支持接近起点的顶点)和贪心算法使用的信息(支持接近目标的顶点)。
在谈论A *时使用的标准术语,g(n)表示从起点到任何顶点的路径的 确切成本 n,h(n)表示从顶点到目标的启发式 估计成本 n。
在上图中,黄色点(h)表示远离目标的顶点,蓝绿色点(g)表示远离起点的顶点。
A* 在从起点移动到目标时平衡两者。每次通过主循环,它检查 n具有最低的顶点 f(n) = g(n) + h(n)。
A* 算法的实现原理
要实现 A* 算法,首先需要将纷繁复杂的游戏地图抽象成寻路网格(如上面的图),最简单的方式是将游戏地图划分为多个正方形单元或正多边形单元,也可以划分为非均匀的凸多边形,这些网格可以看做是一个个 “寻路点”,网格越精细,寻路的效果越好,但计算量也越大,所以针对实际的游戏环境,需要好好平衡一下性能和效果。
A* 算法的基本思想就是借助这些网格实现寻路,从起点开始遍历四周的点,寻找最有可能在最短路径上的点,并以这个点为基准继续向四周遍历,直至遍历到终点,路径也就找到了。
通过这个思想也可以看出,A* 算法其实只能得到一种近似最优解,实际上对于寻路问题,往往存在不止一个最优解,如果非要找出所有的解就只能遍历所有可能的路径一一比较,但这样效率太低,所以 A* 算法并不去遍历整个地图,而是只遍历了最短路径上的点和其周围的点,所以得到的是一种近似最优解。
那么遍历周围的点时怎样确定哪个点最有可能在最短路径上呢?这就是 A* 算法的核心:F=G+H
每个寻路点都有 F、G、H 这三个属性,F 可以理解为通过这个点的总代价,代价越低,这个点当然就更有可能在最短路径上。G 是从起点到这个点的代价,H 是从这个点到终点的代价,这两个代价加起来就是这个点的总代价,关于具体如何计算,下面给出示例。
我们还需要两个集合,一个是 open 集合,一个是 close 集合,open 集合里存放的是还未计算代价的点,close 集合里是已经计算过的点。开始时 open 集合里只有起点,close 集合没有元素,每次迭代将 open 集合里 F 最小的点作为基点,对于基点周围的相邻点做如下处理:
(1)如果这个点是障碍,直接无视。
(2)如果这个点不在 open 表和 close 表中,则加入 open 表
(3)如果这个点已经在 open 表中,并且当前基点所在路径代价更低,则更新它的 G 值和父亲
(4)如果这个点在 close 表中,忽略。
处理完之后将基点加入 close 集合。
当终点出现在 open 表中的时候,迭代结束。
如果到达终点前 open 表空了,说明没有路径可以到达终点。
正文
A* 算法实现
下面来动手实现最简单的 A* 算法,A* 算法针对实际开发有着相当多的变化,怎样设计跟游戏的需求有关,这里用 unity 来实现一个最基本的 2D 正方形网格寻路,实际开发中也可以直接使用 unity 的导航网格或者 A* Pathfinding Project 插件。
在这个实现中,我定义了一个 10x10 的网格,网格中有一些无法通过的障碍。
public class Point
{
public int X;
public int Y;
public int F;
public int G;
public int H;
public Point parent=null;
public bool isObstacle = false;
public Point(int x,int y)
{
X = x;
Y = y;
}
public void SetParent(Point parent,int g)
{
this.parent = parent;
G = g;
F = G + H;
}
}这里定义了一个 Point 类代表每一个寻路点,X 和 Y 代表坐标,F、G、H 就是上面说的三个属性,isObstacle 代表这个点是否是障碍(无法通过),parent 则代表这个点的父亲结点,每当我们遍历到下一个可能在最短路径上的点时,就把它的父亲设为当前结点,这样寻路结束后我们可以从终点通过访问父亲结点一步步回溯到起点,将路径存储下来。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class AStar : MonoBehaviour
{
public const int width = 10;
public const int height = 10;
public Point[,] map = new Point[height,width];
public SpriteRenderer[,] sprites = new SpriteRenderer[height, width];//图片和结点一一对应
public GameObject prefab; //代表结点的图片
public Point start;
public Point end;
void Start()
{
InitMap();
//测试代码
AddObstacle(2, 4);
AddObstacle(2, 3);
AddObstacle(2, 2);
AddObstacle(2, 0);
AddObstacle(6, 4);
AddObstacle(8, 4);
SetStartAndEnd(0, 0, 7, 7);
FindPath();
ShowPath();
}
public void InitMap()//初始化地图
{
for(int i=0;i<width;i++)
{
for (int j = 0; j < height; j++)
{
sprites[i, j] = Instantiate(prefab, new Vector3(i, j, 0),Quaternion.identity).GetComponent<SpriteRenderer>();
map[i, j] = new Point(i, j);
}
}
}
public void AddObstacle(int x,int y)//添加障碍
{
map[x, y].isObstacle = true;
sprites[x, y].color = Color.black;
}
public void SetStartAndEnd(int startX,int startY,int endX,int endY)//设置起点和终点
{
start = map[startX,startY];
sprites[startX, startY].color = Color.green;
end = map[endX, endY];
sprites[endX, endY].color = Color.red;
}
public void ShowPath()//显示路径
{
Point temp = end.parent;
while(temp!=start)
{
sprites[temp.X, temp.Y].color = Color.gray;
temp = temp.parent;
}
}
public void FindPath()
{
List<Point> openList = new List<Point>();
List<Point> closeList = new List<Point>();
openList.Add(start);
while(openList.Count>0)//只要开放列表还存在元素就继续
{
Point point = GetMinFOfList(openList);//选出open集合中F值最小的点
openList.Remove(point);
closeList.Add(point);
List<Point> SurroundPoints = GetSurroundPoint(point.X,point.Y);
foreach(Point p in closeList)//在周围点中把已经在关闭列表的点删除
{
if(SurroundPoints.Contains(p))
{
SurroundPoints.Remove(p);
}
}
foreach (Point p in SurroundPoints)//遍历周围的点
{
if (openList.Contains(p))//周围点已经在开放列表中
{
//重新计算G,如果比原来的G更小,就更改这个点的父亲
int newG = 1 + point.G;
if(newG<p.G)
{
p.SetParent(point, newG);
}
}
else
{
//设置父亲和F并加入开放列表
p.parent = point;
GetF(p);
openList.Add(p);
}
}
if (openList.Contains(end))//只要出现终点就结束
{
break;
}
}
}
public List<Point> GetSurroundPoint(int x,int y)//得到一个点周围的点
{
List<Point> PointList = new List<Point>();
if(x>0&&!map[x-1,y].isObstacle)
{
PointList.Add(map[x - 1, y]);
}
if(y>0 && !map[x , y-1].isObstacle)
{
PointList.Add(map[x, y - 1]);
}
if(x<height-1 && !map[x + 1, y].isObstacle)
{
PointList.Add(map[x + 1, y]);
}
if(y<width-1 && !map[x , y+1].isObstacle)
{
PointList.Add(map[x, y + 1]);
}
return PointList;
}
public void GetF(Point point)//计算某个点的F值
{
int G = 0;
int H = Mathf.Abs(end.X - point.X) + Mathf.Abs(end.Y - point.Y);
if(point.parent!=null)
{
G = 1 + point.parent.G;
}
int F = H + G;
point.H = H;
point.G = G;
point.F = F;
}
public Point GetMinFOfList(List<Point> list)//得到一个集合中F值最小的点
{
int min = int.MaxValue;
Point point = null;
foreach(Point p in list)
{
if(p.F<min)
{
min = p.F;
point = p;
}
}
return point;
}
}上面是 A* 算法的代码,这里使用了一张 100x100 像素的图片代表每一个结点,修改它们的颜色用来表示起点、终点、障碍和路径。在这里我计算的方式是每移动一个格子代价为 1,所以起点的 G 值为 0,每次遍历把 G+1,H 则是当前结点和终点在 x 轴和 y 轴上的差之和。
最终效果
寻路前
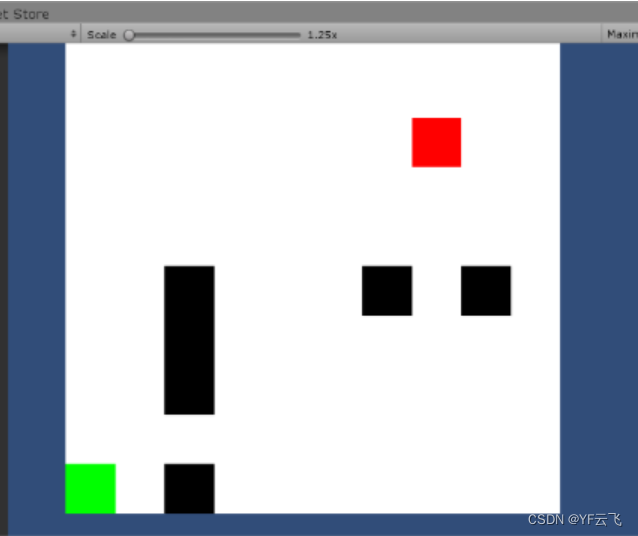
寻路结果

总结
A* 寻路有相当多可以扩展的地方,只要抓住核心,就是不断计算周围点的代价,找出花费最小代价到达终点的路径,这个代价可以针对各种复杂的情况采取不同的计算方法。
比如对于一个 FPS 游戏的 AI而言,游戏中玩家肯定会向火力范围内的敌人攻击,这时候如果为了走最短的路径而暴露在玩家的枪口下就得不偿失了,这时可以加大处在玩家攻击范围内的点的代价值,让 AI 在更短路径和受到攻击的风险之间做出权衡,或者某个地方有奖励道具,这时可以减少奖励道具附近的点的代价值,让 AI 更倾向于绕一些路去获取道具。
总之,理解了算法思想,才能为灵活运用于各种寻路情境打下基础。