LeetCode598. 范围求和 II（python）

news2024/7/6 19:58:26

题目

给你一个 m x n 的矩阵 M ，初始化时所有的 0 和一个操作数组 op ，其中 ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。
提示:
1 <= m, n <= 4 * 104
0 <= ops.length <= 104
ops[i].length == 2
1 <= ai <= m
1 <= bi <= n
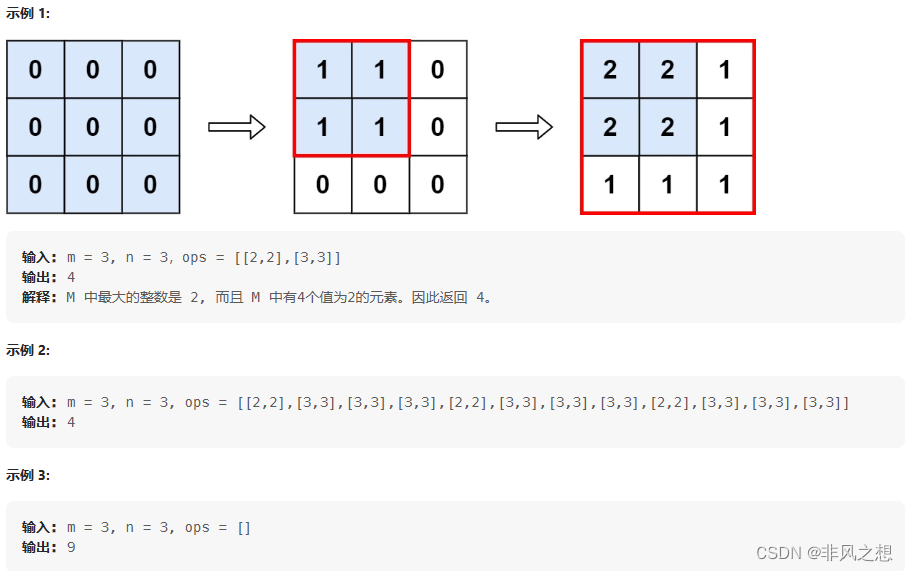
示例
在这里插入图片描述

思路

最简单的思路就是把这个二维数组，也就是加完1之后的矩阵计算出来，在求解最大值的个数

class Solution:
    def maxCount(self, m: int, n: int, ops: List[List[int]]) -> int:
        if not bool(ops):
            return m * n
        elif len(ops) == 1:
            return ops[0][1] * ops[0][0]
        M = [[0 for i in range(n)] for j in range(m)]
        for op in ops:
            ai, bi = op[0], op[1]
            for x in range(m):
                for y in range(n):
                    if x < ai and y < bi:
                        M[x][y] += 1 
        res = sum(M, [])
        return res.count(max(res))

很可惜，超时了，后面的数字太大了，

那么有没有一种只求答案不计算这个数组的方法呢

如果每个x和y在ops[i][0]和ops[i][1]范围内都要加1，
那么其中的最小值就是加1次数最多的，
将ops变成两个分别存放x,y的数组，

res = sum(ops, []) #将ops改为一维数组
res[::2] #索引为奇数，为x的数组
res[1::2] #索引为偶数，为y的数组

分别求出x和y的最小值，

min(res[::2]）
min(res[1::2])

x_min * y_min就是加1次数最多的矩阵，
x_min * y_min 的值就是最大值的个数

min(res[1::2]) * min(res[::2])

当然还要考虑到ops为空的情况，
每个值都没有+1 ，
所以直接返回 x_min * y_min

if not bool(ops):
            return m * n

题解

class Solution:
    def maxCount(self, m: int, n: int, ops: List[List[int]]) -> int:
        if not bool(ops):
            return m * n
        else:
            res = sum(ops, [])
            return min(res[1::2]) * min(res[::2])


https://leetcode.cn/problems/range-addition-ii/solutions/2162215/fan-wei-qiu-he-by-funny-shavvpwo-i3xg/