【C++进阶】四、红黑树（三）

news2024/12/25 1:32:13

目录

一、红黑树的概念

二、红黑树的性质

三、红黑树节点的定义

四、红黑树的插入

五、红黑树的验证

六、红黑树与AVL树的比较

七、完整代码

一、红黑树的概念

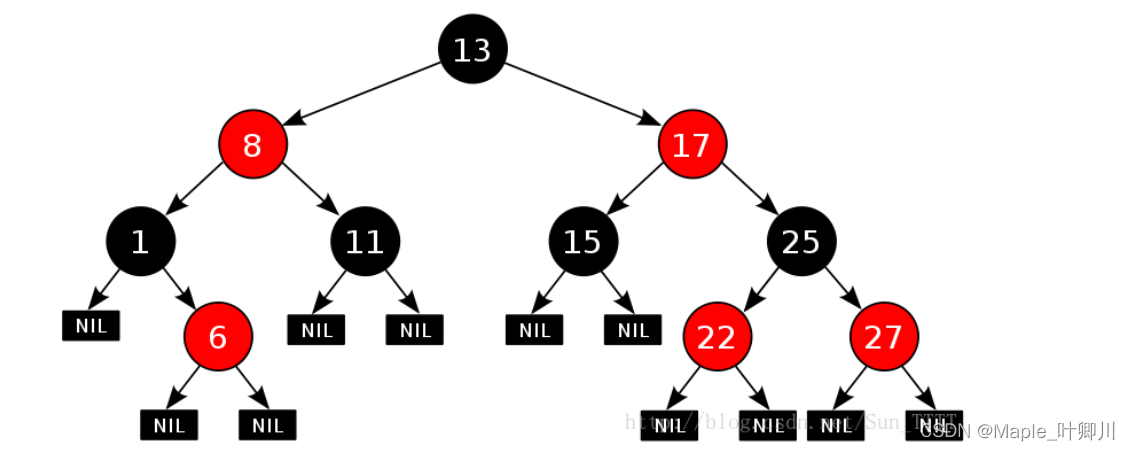
        红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的

如下图就是一棵红黑树：

二、红黑树的性质

红黑树有以下性质：

  1. 每个结点不是红色就是黑色
  2. 根节点是黑色的
  3. 如果一个节点是红色的，则它的两个孩子结点是黑色的，即没有连续红色节点
  4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
  5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点，如上图的NIL节点)
  •  红黑树最优情况（左右平衡）：全黑或每条路径都是一黑一红相间的满二叉树，搜索高度 logN
  • 红黑树最差情况（左右极不平衡）：每颗子树左子树全黑，右子树一黑一红，搜索高度 2*logN

        红黑树不追求极致的平衡，AVL树则是追求极致的平衡，红黑树是近似平衡；红黑树这种近似平衡的结构大大减少了大量的旋转，红黑树的综合性能优于 AVL树

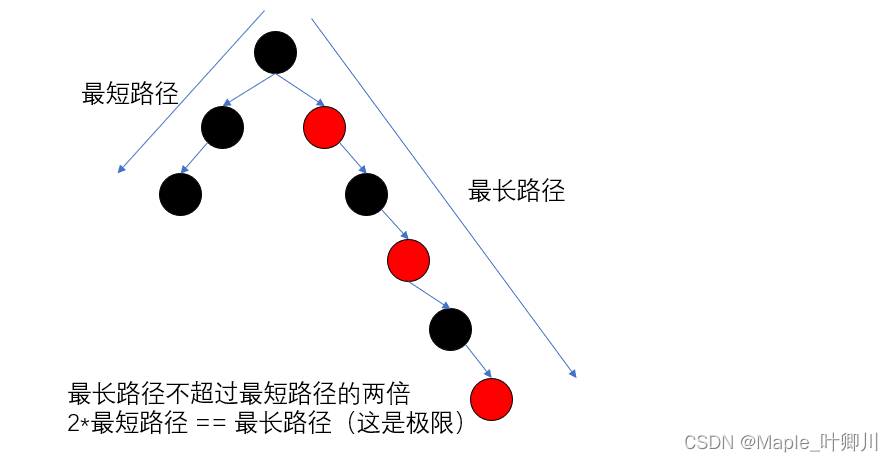
为什么红黑树满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径节点个数的两倍？

  • 红黑树的最短路径：全黑，一条路径上的全是黑色节点
  • 红黑树的最长路径：一黑一红相间的路径

比如：

三、红黑树节点的定义

        红黑树也是使用键值对，即KV模型，也是为了方便后序操作，红黑树的结构也是三叉链，即增加了指向父节点的 parent指针，还增加了一个成员变量，用于标识节点的颜色（red or black）

enum Colour
{
	RED,
	BLACK,
};

//K:key, V:value
template<class K, class V>
struct RBTreeNode
{
	//构造函数
	RBTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_col(RED)
	{}

	//成员变量
	pair<K, V> _kv;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	Colour _col;
};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:

private:
	Node* _root = nullptr;//缺省值
};

注：这里使用了枚举来列举颜色

为什么构造红黑树结点时，默认将结点的颜色设置为红色？

  • 插入结点如果是黑色的，一定破坏红黑树的性质4，无论如何都必须对红黑树进行调整。
  • 插入结点如果是红色的，可能破坏红黑树的性质3，可能需要对红黑树进行调整 或者不需要调整

所以将节点颜色默认设置为红色

四、红黑树的插入

红黑树的插入分两步：

  1. 按照二叉搜索树的方式插入新节点
  2. 判断是否需要对红黑树进行调整

（1）插入节点

因为红黑树本身就是一棵二叉搜索树，因此寻找结点的插入位置是非常简单的，按照二叉搜索树的插入规则：

  1. 待插入结点的key值比当前结点小就插入到该结点的左子树
  2. 待插入结点的key值比当前结点大就插入到该结点的右子树
  3. 待插入结点的key值与当前结点的 key 值相等就插入失败

（2）判断是否需要对红黑树进行调整

判断：插入节点的父亲 parent 存在且为红色，则需要进行调整，否则不需要

然后分两种情况：

  • （A）parent在 grandfather 的左边
  • （B）parent在 grandfather 的右边

注：进行调整的关键是 uncle 

（A）parent在 grandfather 的左边有三种情况：

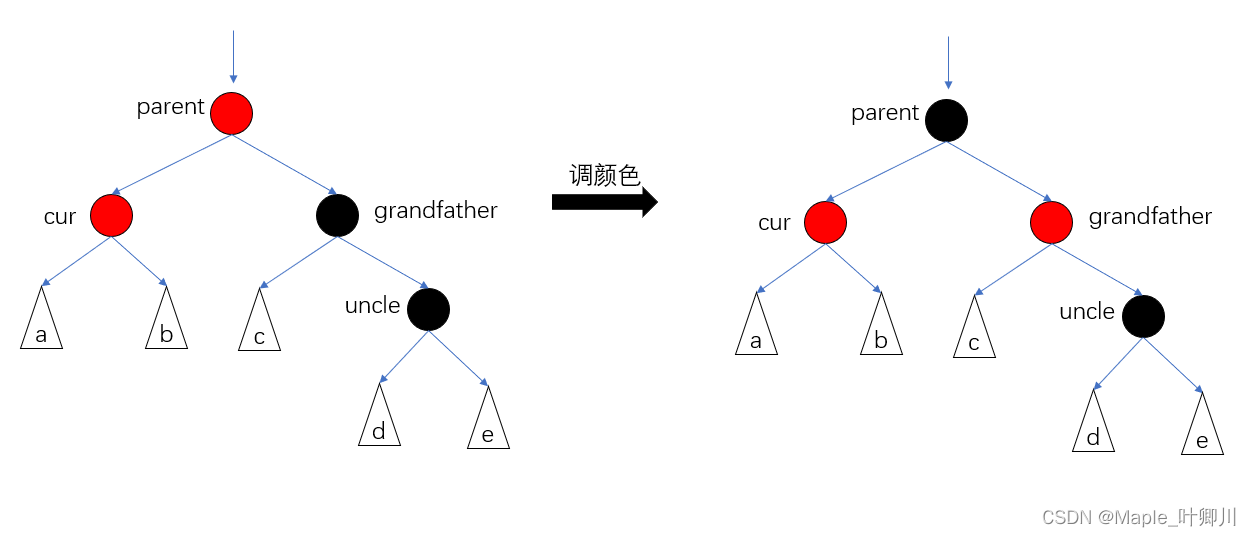
  1. 情况1：uncle存在且为红，uncle和parent的颜色需要修改为黑，granfather 修改为红，如果满足循环条件继续往上更新
  2. 情况2：uncle存在且为黑，需要对红黑树进行旋转
  3. 情况3：uncle不存在，需要对红黑树进行旋转

情况1，图如下：

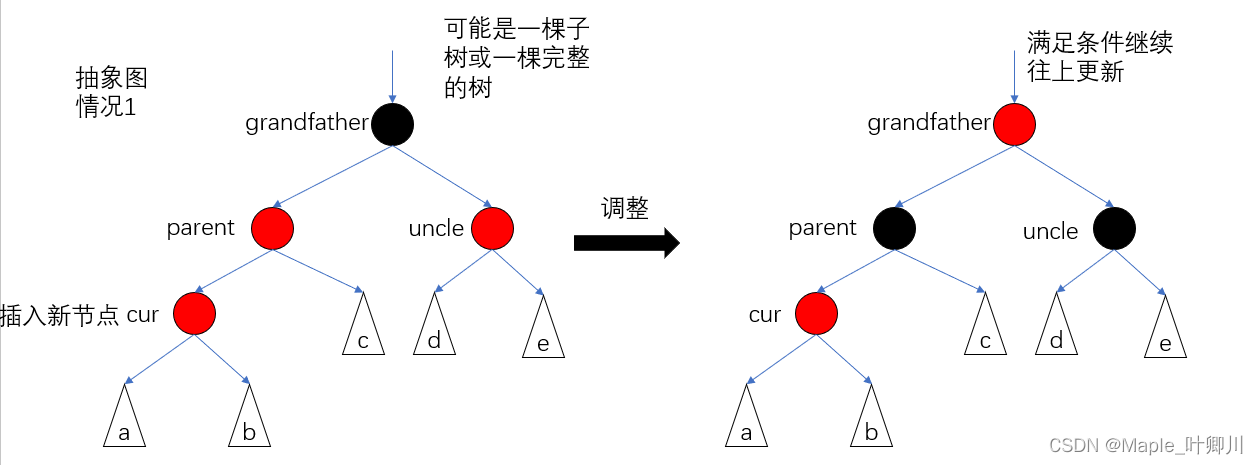
注：情况2和情况3是一起处理的

情况2 + 情况3：

  1. cur，parent，grandfather 三个节点在一条直线上，单旋处理即可，对 grandfater 进行右单旋，然后 parent 的颜色改为黑，grandfater 的颜色改为红
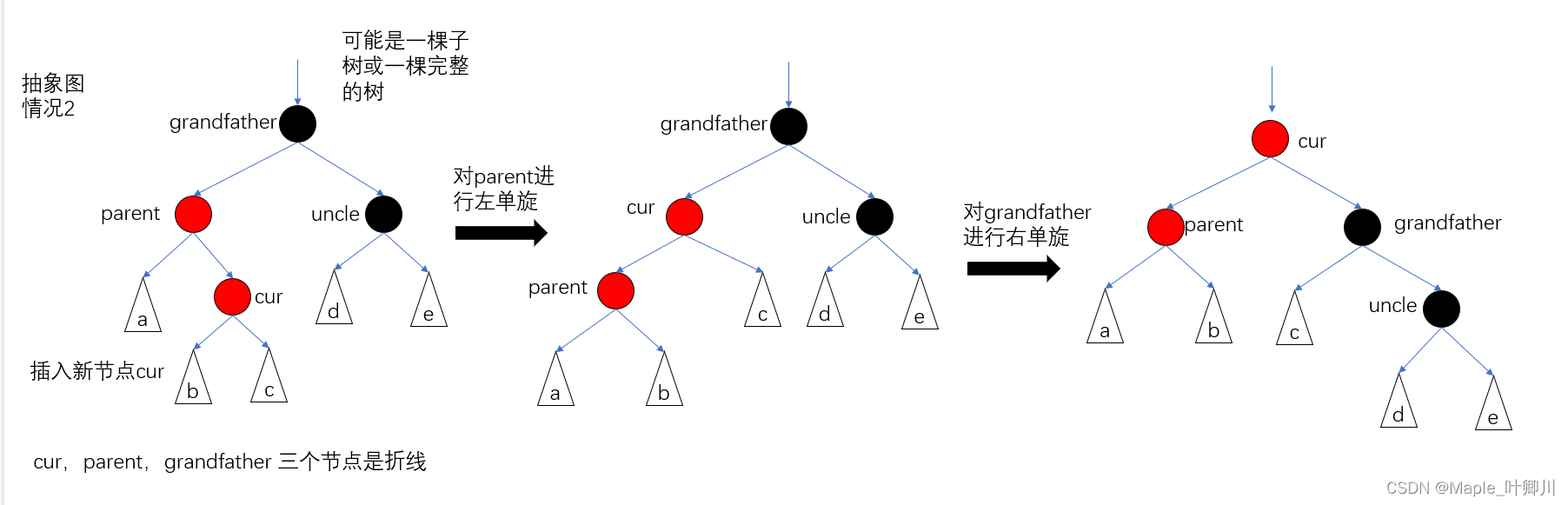
  2. cur，parent，grandfather 三个节点是折线，需要双旋处理，对 parent 进行左单旋，然后对 grandfater 进行右单旋，然后 cur 的颜色改为黑，grandfater 的颜色改为红

情况2，图如下：

cur，parent，grandfather 三个节点在一条直线上

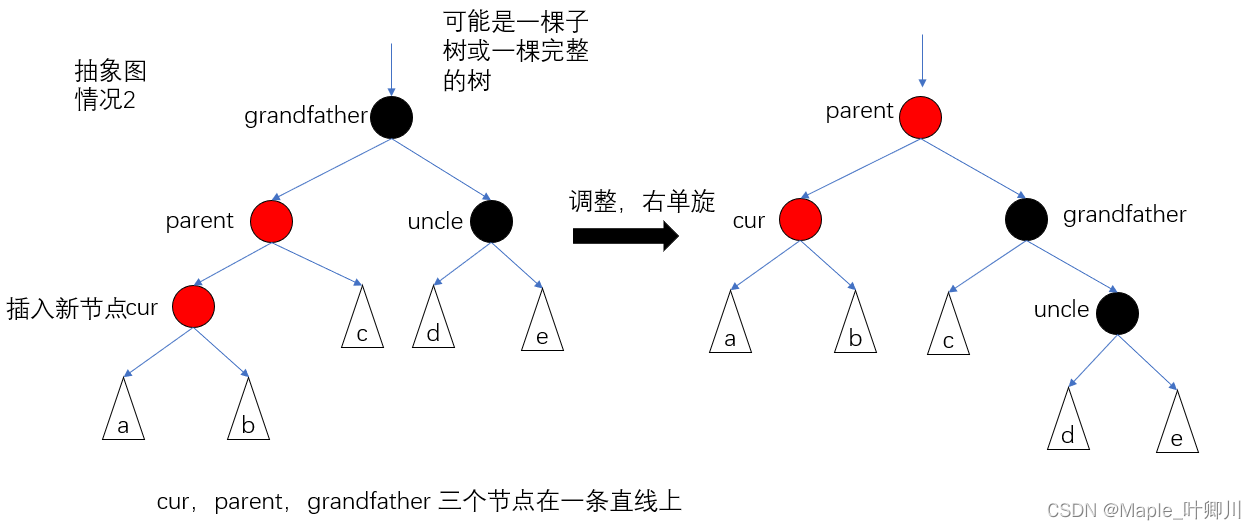
调颜色 

 cur，parent，grandfather 三个节点是折线

 调颜色

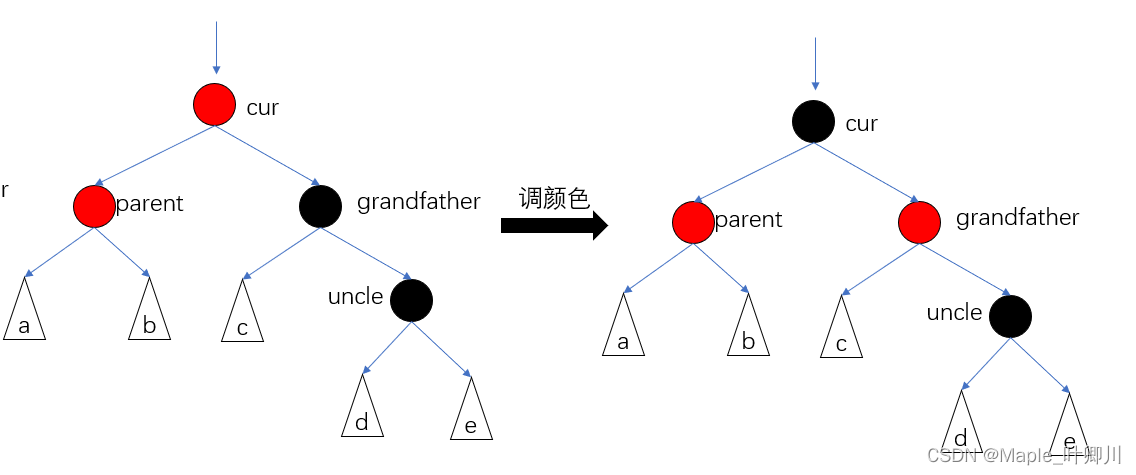
 情况3，图如下：

cur，parent，grandfather 三个节点在一条直线上

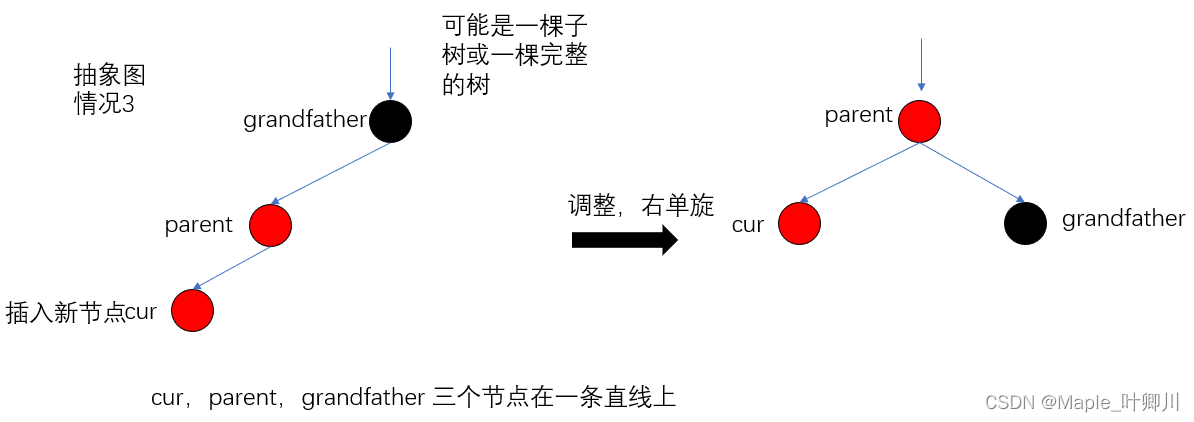
调颜色

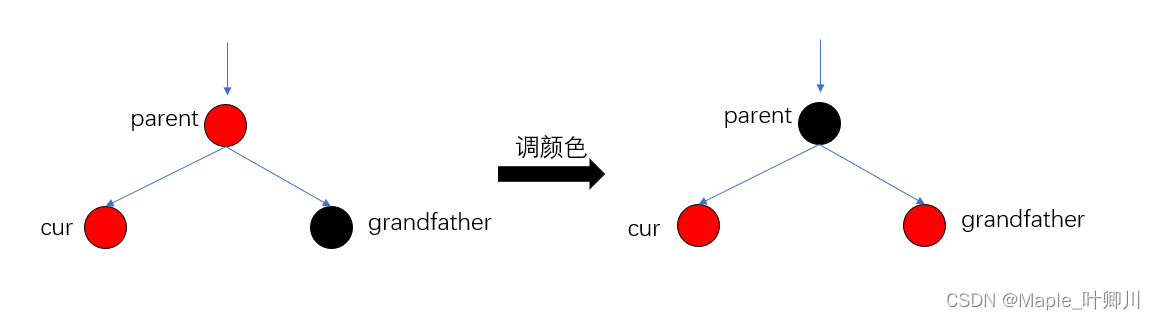
  cur，parent，grandfather 三个节点是折线

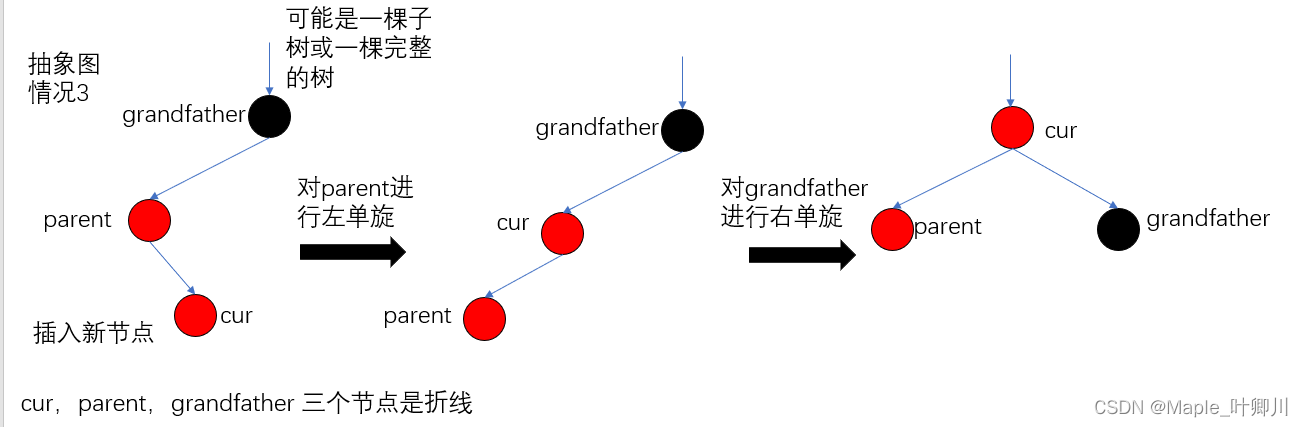
 调颜色

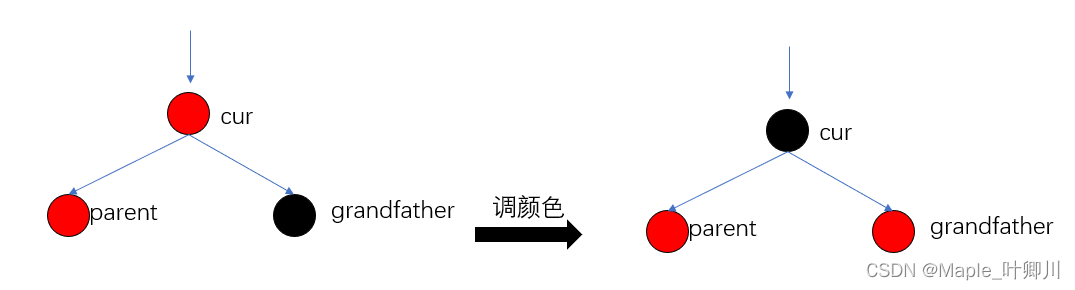
（B）parent在 grandfater 的右边也有三种情况：（与左边情况完全一致，只是旋转不同）

  1. 情况1：uncle存在且为红，uncle和parent的颜色需要修改为黑，grandfater修改为红，如果满足循环条件继续往上更新
  2. 情况2：uncle存在且为黑，需要对红黑树进行旋转，对 grandfather 进行右单旋
  3. 情况3：uncle不存在，需要对红黑树进行双旋转，对 parent 进行左单旋，然后对 grandfather 进行右单旋

注：情况2和情况3是一起处理的

情况2 + 情况3：

  1. cur，parent，grandfather 三个节点在一条直线上，单旋处理即可，对 grandfather 进行左单旋，然后 parent 的颜色改为黑，grandfater 的颜色改为红
  2. cur，parent，grandfather 三个节点是折线，需要双旋处理，对 parent 进行右单旋，然后对 grandfather 进行左单旋，然后 cur 的颜色改为黑，grandfather 的颜色改为红

图就不画了，左边的图反过来就是右边的图，旋转在 AVL树有解释，这里就不再解释

经调整后，保持了红黑树的特性

插入代码如下：

//插入
bool Insert(const pair<K, V>& kv)
{
	//节点为空，新建根节点
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_root->_col = BLACK;//根节点默认为黑色
		return true;
	}

	//节点为不空
	Node* parent = nullptr;//用于记录上一个节点
	Node* cur = _root;
	//寻找合适的位置进行插入
	while (cur)
	{
		if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else//cur->kv.first == kv.first要插入值已经存在，插入失败
		{
			return false;
		}
	}

	cur = new Node(kv);
	cur->_col = RED;//新节点默认为红
	//插入
	if (parent->_kv.first < kv.first)//插入到parent左边
	{
		parent->_right = cur;
		cur->_parent = parent;
	}
	else//插入到parent右边
	{
		parent->_left = cur;
		cur->_parent = parent;
	}

	//进行调平衡 && 保持红黑树的特性，即插入节点的父亲是红色，需要对红黑树进行调整
	while (parent && parent->_col == RED)//parent存在且为红 进行调整
	{
		Node* grandfather = parent->_parent;

		//（1）parent在grandfater的左边
		//（2）parent在grandfater的右边

		if (parent == grandfather->_left)//parent在grandfater的左边
		{
			//情况1：uncle存在且为红，uncle和parent的颜色需要修改为黑，grandfater修改为红，如果满足循环条件继续往上更新
			//情况2：uncle存在且为黑，需要对红黑树进行旋转
			//情况3：uncle不存在，需要对红黑树进行旋转
			//注：情况2和情况3是一起处理的

			Node* uncle = grandfather->_right;
			if (uncle && uncle->_col == RED)//情况1
			{
				//修改颜色
				uncle->_col = parent->_col = BLACK;
				grandfather->_col = RED;
				//迭代往上更新
				cur = grandfather;
				parent = cur->_parent;
			}
			else//情况2 + 情况3
			{
				if (cur == parent->_left)//cur，parent，grandfater三个节点在一条直线上，单旋处理即可
				{
					RotateR(grandfather);//右单旋
					parent->_col = BLACK;
					grandfather->_col = RED;
				}
				else//cur，parent，grandfater三个节点是折线，需要双旋处理
				{
					RotateL(parent);//左单旋
					RotateR(grandfather);//右单旋
					cur->_col = BLACK;
					grandfather->_col = RED;
				}
				break;//旋转后，该子树的根变成了黑色，符合红黑树的特性，无需继续往上处理
			}
		}
		else//parent在grandfater的右边
		{
			//在右边 也是上面左边的三种情况
			Node* uncle = grandfather->_left;
			if (uncle && uncle->_col == RED)//情况1
			{
				//修改颜色
				uncle->_col = parent->_col = BLACK;
				grandfather->_col = RED;
				//迭代往上更新
				cur = grandfather;
				parent = cur->_parent;
			}
			else//情况2 + 情况3
			{
				if (cur == parent->_right)//cur，parent，grandfater三个节点在一条直线上，单旋处理即可
				{
					RotateL(grandfather);
					parent->_col = BLACK;
					grandfather->_col = RED;
				}
				else//cur，parent，grandfater三个节点是折线，需要双旋处理
				{
					RotateR(parent);
					RotateL(grandfather);
					cur->_col = BLACK;
					grandfather->_col = RED;
				}
				break;//旋转后，该子树的根变成了黑色，符合红黑树的特性，无需继续往上处理
			}
		}
	}

	_root->_col = BLACK;//根的颜色需要变为黑（原因是可能情况1会把根节点变红）
	return true;
}

注：红黑树其他接口就不实现了，在面试考的花也是考查红黑树的插入，即红黑树如何调平衡

五、红黑树的验证

红黑树的检测分为两步：

  1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
  2. 检测其是否满足红黑树的性质

（1）中序检查

//中序遍历
void InOrder()
{
	_InOrder(_root);
}

void _InOrder(Node* root)
{
	if (root == nullptr)
		return;

	_InOrder(root->_left);
	cout << root->_kv.first << ":" << root->_kv.second << endl;
	_InOrder(root->_right);
}

（2）检查红黑树特性

//检查红黑树特性
bool IsBalance()
{
	if (_root == nullptr)
	{
		return true;
	}

	if (_root->_col != BLACK)
	{
		cout << "违反规则：根节点不为黑色" << endl;
		return false;
	}

	Node* left = _root;
	int ref = 0;//用于一条路径上记录黑色节点的数量
	while (left)//求一条路径的黑色节点
	{
		if (left->_col == BLACK)
		{
			++ref;
		}
		left = left->_left;
	}
	return Check(_root, 0, ref);
}

//检查每条路径的黑色节点是否相等 && 是否出现连续红色节点
bool Check(Node* root, int blackNum, int ref)
{
	if (root == nullptr)
	{
		if (blackNum != ref)
		{
			cout << "违反规则：本条路径的黑色节点的数量跟最左路径不相等" << endl;
			return false;
		}
		return true;
	}

	if (root->_col == RED && root->_parent->_col == RED)
	{
		cout << "违反规则：出现连续红色节点" << endl;
		return false;
	}

	if (root->_col == BLACK)
	{
		++blackNum;
	}

	return Check(root->_left, blackNum, ref)
		&& Check(root->_right, blackNum, ref);
}

六、红黑树与AVL树的比较

        红黑树和 AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(logN)，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比 AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多

红黑树的应用：

  1. C++ STL库 -- map/set、mutil_map/mutil_set
  2. Java 库
  3. linux内核
  4. 其他一些库

七、完整代码

RBTree.h

#pragma once

enum Colour
{
	RED,
	BLACK,
};

//K:key, V:value
template<class K, class V>
struct RBTreeNode
{
	//构造函数
	RBTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_col(RED)
	{}

	//成员变量
	pair<K, V> _kv;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	Colour _col;
};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	//插入
	bool Insert(const pair<K, V>& kv)
	{
		//节点为空，新建根节点
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;//根节点默认为黑色
			return true;
		}

		//节点为不空
		Node* parent = nullptr;//用于记录上一个节点
		Node* cur = _root;
		//寻找合适的位置进行插入
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else//cur->kv.first == kv.first要插入值已经存在，插入失败
			{
				return false;
			}
		}

		cur = new Node(kv);
		cur->_col = RED;//新节点默认为红
		//插入
		if (parent->_kv.first < kv.first)//插入到parent左边
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else//插入到parent右边
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

		//进行调平衡 && 保持红黑树的特性，即插入节点的父亲是红色，需要对红黑树进行调整
		while (parent && parent->_col == RED)//parent存在且为红 进行调整
		{
			Node* grandfather = parent->_parent;

			//（1）parent在grandfater的左边
			//（2）parent在grandfater的右边

			if (parent == grandfather->_left)//parent在grandfater的左边
			{
				//情况1：uncle存在且为红，uncle和parent的颜色需要修改为黑，grandfater修改为红，如果满足循环条件继续往上更新
				//情况2：uncle存在且为黑，需要对红黑树进行旋转
				//情况3：uncle不存在，需要对红黑树进行旋转
				//注：情况2和情况3是一起处理的

				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)//情况1
				{
					//修改颜色
					uncle->_col = parent->_col = BLACK;
					grandfather->_col = RED;
					//迭代往上更新
					cur = grandfather;
					parent = cur->_parent;
				}
				else//情况2 + 情况3
				{
					if (cur == parent->_left)//cur，parent，grandfater三个节点在一条直线上，单旋处理即可
					{
						RotateR(grandfather);//右单旋
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else//cur，parent，grandfater三个节点是折线，需要双旋处理
					{
						RotateL(parent);//左单旋
						RotateR(grandfather);//右单旋
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;//旋转后，该子树的根变成了黑色，符合红黑树的特性，无需继续往上处理
				}
			}
			else//parent在grandfater的右边
			{
				//在右边 也是上面左边的三种情况
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)//情况1
				{
					//修改颜色
					uncle->_col = parent->_col = BLACK;
					grandfather->_col = RED;
					//迭代往上更新
					cur = grandfather;
					parent = cur->_parent;
				}
				else//情况2 + 情况3
				{
					if (cur == parent->_right)//cur，parent，grandfater三个节点在一条直线上，单旋处理即可
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else//cur，parent，grandfater三个节点是折线，需要双旋处理
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;//旋转后，该子树的根变成了黑色，符合红黑树的特性，无需继续往上处理
				}
			}
		}

		_root->_col = BLACK;//根的颜色需要变为黑（原因是可能情况1会把根节点变红）
		return true;
	}
	//中序遍历
	void InOrder()
	{
		_InOrder(_root);
	}
	//检查红黑树特性
	bool IsBalance()
	{
		if (_root == nullptr)
		{
			return true;
		}

		if (_root->_col != BLACK)
		{
			cout << "违反规则：根节点不为黑色" << endl;
			return false;
		}

		Node* left = _root;
		int ref = 0;//用于一条路径上记录黑色节点的数量
		while (left)//求一条路径的黑色节点
		{
			if (left->_col == BLACK)
			{
				++ref;
			}
			left = left->_left;
		}
		return Check(_root, 0, ref);
	}
private:
	//检查每条路径的黑色节点是否相等 && 是否出现连续红色节点
	bool Check(Node* root, int blackNum, int ref)
	{
		if (root == nullptr)
		{
			if (blackNum != ref)
			{
				cout << "违反规则：本条路径的黑色节点的数量跟最左路径不相等" << endl;
				return false;
			}
			return true;
		}

		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "违反规则：出现连续红色节点" << endl;
			return false;
		}

		if (root->_col == BLACK)
		{
			++blackNum;
		}

		return Check(root->_left, blackNum, ref)
			&& Check(root->_right, blackNum, ref);
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_InOrder(root->_right);
	}
	//左单旋
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		//进行链接
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		Node* ppNode = parent->_parent;//记录parent节点的前一个节点
		subR->_left = parent;
		parent->_parent = subR;

		if (ppNode == nullptr)//即subR已经是根节点
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else//subR不是根节点
		{
			//与上一个节点进行链接
			if (ppNode->_left == parent)//parent原本在 ppNode 的左边
			{
				ppNode->_left = subR;
			}
			else//parent原本在 ppNode 的右边
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}
	}
	//右单旋
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		//进行链接
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		Node* ppNode = parent->_parent;//记录parent节点的前一个节点
		subL->_right = parent;
		parent->_parent = subL;

		if (ppNode == nullptr)//即subL已经是根节点
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else//subR不是根节点
		{
			//与上一个节点进行链接
			if (ppNode->_left == parent)//parent原本在 ppNode 的左边
			{
				ppNode->_left = subL;
			}
			else//parent原本在 ppNode 的右边
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
	}
private:
	Node* _root = nullptr;//缺省值
};

 Test.cpp

#include <iostream>
using namespace std;
#include "RBTree.h"

void TestRBTree1()
{
	//int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
	//int arr[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	RBTree<int, int> t;
	for (auto e : arr)
	{
		t.Insert(make_pair(e, e));
	}
	t.InOrder();
}

void TestRBTree2()
{
	srand(time(0));//随机数种子
	const size_t N = 100000;
	RBTree<int, int> t;
	for (size_t i = 0; i < N; ++i)
	{
		size_t x = rand();
		t.Insert(make_pair(x, x));
		//cout << t.IsBalance() << endl;
	}
	cout << t.IsBalance() << endl;
}

int main()
{
	TestRBTree2();
	return 0;
}

----------------我是分割线---------------

文章到这里就结束了，下一篇即将更新

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/403930.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

嵌入式安防监控项目——html框架分析和环境信息刷新到网页

嵌入式安防监控项目——html框架分析和环境信息刷新到网页

目录 一、html控制LED 二、模拟数据上传到html 一、html控制LED 简单来说就是html给boa服务器发了一个控制指令信息&#xff0c;然后boa转发给cgi进程&#xff0c;cgi通过消息队列和主进程通信。主进程再去启动LED子线程。 这是老师给的工程。 以前学32都有这工具那工具来管…
阅读更多...
导航技术调研（CSDN_0023_20221217）

导航技术调研（CSDN_0023_20221217）

文章编号&#xff1a;CSDN_0023_20221217 目录 1. 惯性导航 2. 组合导航技术 3. 卡尔曼滤波 1. 惯性导航 惯性导航系统(INS-Inertial Navigation System)是上个世纪初发展起来的。惯性导航是一种先进的导航方法&#xff0c;但实现导航定位的原理却非常简单&#xff0c;它是…
阅读更多...
RHCSA-用户和组管理和文件系统权限（3.11）

RHCSA-用户和组管理和文件系统权限（3.11）

目录 用户&#xff08;UID&#xff09; 用户类别&#xff08;UID&#xff09;&#xff1a; 用户的增删改查&#xff1a; 修改用户密码&#xff1a; 查看用户是否存在&#xff1a; 组&#xff08;GID&#xff09; 组的增删改查&#xff1a; 设置组密码&#xff1a; 用户…
阅读更多...
idea集成GitHub

idea集成GitHub

设置 GitHub 账号绑定账号有两种方式&#xff1a;1. 通过授权登录2.如果上述登录不成功&#xff0c;用Token口令的方式登录&#xff0c;口令在github账号哪里生成&#xff0c;点击settings --->Developer settings --->pwrsonal access tokens ----> 复制口令到idea 口…
阅读更多...
设置cpp-httplib 服务器模式模式下的线程池大小 以及如何增加默认处理函数 以便能够实现http请求转发

设置cpp-httplib 服务器模式模式下的线程池大小 以及如何增加默认处理函数 以便能够实现http请求转发

先说说默认的创建的线程池数量 原因是某天调试在gdb调试下 一启动程序发现 开启了好多线程 如下图 因为我们程序 没几个线程 数了下 居然有60多个线程 不需要那么多 所以看下 httplib的源码 构造函数的时候 设置了最大线程池数量 看下这个宏 然后打印了下 发现 居然那么大 …
阅读更多...
FusionCompute安装和配置步骤

FusionCompute安装和配置步骤

1. 先去华为官网下载FusionCompute的镜像 下载地址&#xff1a;https://support.huawei.com/enterprise/zh/distributed-storage/fusioncompute-pid-8576912/software/251713663?idAbsPathfixnode01%7C22658044%7C7919788%7C9856606%7C21462752%7C8576912 下载后放在D盘中&am…
阅读更多...
【rabbitmq 实现延迟消息-插件版本安装（docker环境）】

【rabbitmq 实现延迟消息-插件版本安装（docker环境）】

一&#xff1a;插件简介 在rabbitmq 3.5.7及以上的版本提供了一个插件&#xff08;rabbitmq-delayed-message-exchange&#xff09;来实现延迟队列功能。同时插件依赖Erlang/OPT 18.0及以上。 二&#xff1a;插件安装 1&#xff1a;选择适合自己安装mq 版本的插件&#xff1…
阅读更多...
设计模式---抽象工厂模式

设计模式---抽象工厂模式

目录 1 介绍 2 优缺点 3 实现 1 介绍 抽象工厂模式(Abstract Factory Pattern) 是围绕一个超级工厂创建其他工厂。该超级工厂又称为其他工厂的工厂。这种类型的设计模式属于创建型模式&#xff0c;它提供了一种创建对象的最佳方式。 在抽象工厂模式中&#xff0c;接口是负…
阅读更多...
ROC和AUC

ROC和AUC

目录 ROC AUC ROC ROC曲线是Receiver Operating Characteristic Curve的简称&#xff0c;中文名为"受试者工作特征曲线"。ROC曲线的横坐标为假阳性率(False Postive Rate, FPR)&#xff1b;纵坐标为真阳性率(True Positive Rate, TPR).FPR和TPR的计算方法分别为 F…
阅读更多...
Spring——案例-业务层接口执行效率和AOP通知获取数据+AOP总结

Spring——案例-业务层接口执行效率和AOP通知获取数据+AOP总结

执行时间获取:记录开始时间和结束时间&#xff0c;取差值。 这里使用环绕通知来实现。 环境准备: 项目文件结构: 业务层接口和实现类: 数据层: 采用mybatis注解开发&#xff0c;这里没有实现类&#xff0c;直接在接口方法里面实现映射。 domain层: 实现了数据库里面每一个…
阅读更多...
Altium designer--软件简介及安装教程（Altium designer16）

Altium designer--软件简介及安装教程（Altium designer16）

一、软件介绍&#xff08;完整安装包资源见文末链接&#xff0c;含破解license&#xff09; Altium Designer 是一款简单易用、原生3D设计增强的一体化设计环境&#xff0c;结合了原理图、ECAD库、规则和限制条件、BoM、供应链管理、ECO流程和世界一流的PCB设计工具。通过原理…
阅读更多...
Baumer工业相机中曝光与增益两种功能的优点和作用以及使用方法

Baumer工业相机中曝光与增益两种功能的优点和作用以及使用方法

项目场景 Baumer工业相机堡盟相机是一种高性能、高质量的工业相机&#xff0c;可用于各种应用场景&#xff0c;如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能&#xff0c;可以实时传输高分辨率图像。此外&#xff0c;该相机还具有…
阅读更多...
[NOIP2009 提高组] 最优贸易（C++，tarjan，topo，DP）

[NOIP2009 提高组] 最优贸易（C++，tarjan，topo，DP）

题目描述 $C 国有国有国有 n 个大城市和个大城市和个大城市和 m$ 条道路&#xff0c;每条道路连接这 nnn个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 mmm 条道路中有一部分为单向通行的道路&#xff0c;一部分为双向通行的道路&#xff0c;双向通行的…
阅读更多...
OpenHarmony通过MQTT连接 “改版后的华为IoT平台”

OpenHarmony通过MQTT连接 “改版后的华为IoT平台”

一、前言 本篇文章我们使用的是BearPi-HM_Nano开发板：小熊派的主板+E53_IA1扩展板 源码用的是D6_iot_cloud_oc，点击下载BearPi-HM_Nano全量源码 那么为什么要写这篇呢？ 前段时间看到OpenHarmony群里，经常有小伙伴问接入华为IoT平台的问题，他们无法正常连接到华为IoT平台等…
阅读更多...
【数据结构】二叉树相关OJ题

【数据结构】二叉树相关OJ题

文章目录一、单值二叉树二、检查两颗树是否相同三、判断一棵树是否为另一颗树的子树四、对称二叉树五、二叉树的前序遍历六、二叉树中序遍历七、二叉树的后序遍历八、二叉树的构建及遍历一、单值二叉树 单值二叉树 题目描述 如果二叉树每个节点都具有相同的值&#xff0c;那…
阅读更多...
【互联网架构】聊一聊所谓的“跨语言、跨平台“

【互联网架构】聊一聊所谓的“跨语言、跨平台“

文章目录序跨语言跨平台【饭后杂谈】为什么有人说Java的跨平台很鸡肋&#xff1f;序 很多技术都具有跨语言、跨平台的特点 比如JSON是跨语言的、Java是跨平台的、UniAPP、Electron是跨平台的 跨语言和跨平台&#xff0c;是比较重要的一个特性。这些特性经常能够决定开发者是否…
阅读更多...
软件测试项目实战，一比一还原可以写进简历的

软件测试项目实战，一比一还原可以写进简历的

项目一&#xff1a;ShopNC商城 项目概况&#xff1a; ShopNC商城是一个电子商务B2C电商平台系统&#xff0c;功能强大&#xff0c;安全便捷。适合企业及个人快速构建个性化网上商城。 包含PCIOS客户端Adroid客户端微商城&#xff0c;系统PC后台是基于ThinkPHP MVC构架开发的跨…
阅读更多...
ubuntu-22.04.2网络配置和root登录和root远程ssh登录

ubuntu-22.04.2网络配置和root登录和root远程ssh登录

配置网络&#xff1a; 1.查看网卡名称 ip addr(ifconfig 无法使用&#xff0c;需要后期安装) 2. 配置静态IP &#xff08;1&#xff09;进入网络配置文件&#xff1a; vim /etc/netplan/00-installer-config.yaml &#xff08;2&#xff09;按一下 i ,进入插入模式&#…
阅读更多...
网络 | 数据链路层讲解 | MAC帧与APR协议

网络 | 数据链路层讲解 | MAC帧与APR协议

最大以太网帧大小指的是以太网帧从目的地址到冗余校验的总字节数。在802.3标准里&#xff0c;规定了一个以太网帧的数据部分(Payload)的最大长度是1500个字节&#xff0c;这个数也是MTU。在这个限制之下&#xff0c;最长的以太网帧包括6字节的目的地址(DMAC)、6字节的源地址(SM…
阅读更多...
【C++】list的模拟实现

【C++】list的模拟实现

文章目录1.list 底层2. list的模拟实现1. list_node 类设计2. list类如何调用类型3 .push_back(正常实现)4. 迭代器的实现第一个模板参数Tconst迭代器第二个模板参数Ref第三个模板参数Ptr对list封装的理解5. insert6.push_back与 push_front(复用)7. erase8. pop_back与pop_fro…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023