题目描述

$C $国有$ n $个大城市和$ m$ 条道路，每条道路连接这 $n$个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 $m$ 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 $1 $条。

$C $国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 $C$ 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 $C$ 国 n 个城市的标号从 $1\sim n$，阿龙决定从 $1 $号城市出发，并最终在 $n$ 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 $n$ 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 $C$ 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 $C $国有 $5$个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

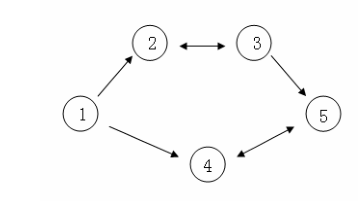
假设 $1n$ 号城市的水晶球价格分别为 $4,3,5,6,1$。

阿龙可以选择如下一条线路：$1$->$2$->$3$->$5$，并在 $2 $号城市以$ 3$ 的价格买入水晶球，在 $3$号城市以$ 5 $的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路$ 1$->$4$->$5$->$4$->$5$，并在第$1 $次到达$ 5$ 号城市时以 $1 $的价格买入水晶球，在第 $2$ 次到达$ 4$ 号城市时以$ 6$ 的价格卖出水晶球，赚取的旅费数为$ 5$。

现在给出 $n $个城市的水晶球价格，$m$ 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入格式

第一行包含 $2$ 个正整数$ n $和 $m$，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 $m$ 行，每行有$ 3 $个正整数$x,y,z$，每两个整数之间用一个空格隔开。如果 $z=1$，表示这条道路是城市$ x $到城市$ y $之间的单向道路；如果$ z=2$，表示这条道路为城市 $x $和城市$y $之间的双向道路。

输出格式

一 个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 $0$。

样例 #1

样例输入 #1

5 5 
4 3 5 6 1 
1 2 1 
1 4 1 
2 3 2 
3 5 1 
4 5 2

样例输出 #1

5

提示

【数据范围】

输入数据保证 $1$ 号城市可以到达$ n $号城市。

对于 10%的数据，$1\le n\le 6$。

对于 30%的数据，$1\le n\le 100$。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据，$1\le n\le 100000$，$1\le m\le 500000$，$1\le x$，$y\le n$，$1\le z\le 2$，$1\le$各城市

水晶球价格$\le 100$。

NOIP 2009 提高组 第三题

解题思路：

不需要过多考虑，本题唯一的解法是遍历每一种情况，找出最大差价

关于图的搜索，如果一个点能被重复经过会使问题复杂化，所以我们首先缩点，简化问题

然后考虑如何得出答案

缩点需要保留的信息是环中的最大出手价格和最小入手价格

DFS从城市1开始暴力搜索记录当前行过点中最小的买入价格，每到一个点，计算差价

然后与当前的最大差价比较（差价最小为0，代表不需要贸易）

需要注意的是，我们的目标除了找出最大差价，还需要到达城市n，否则答案没有意义

思路非常简洁，当然判题的回复也非常简洁

TLE（QAQ）

那么就需要考虑如何优化

超时的原因一定是因为暴力搜索重复搜索了太多次，所以关键在于去重

所以想到动态规划

考虑以上的图，动态规划关键在于从子情况的解推导出下一个情况的解

而我们从$1$开始DFS会导致直接到达$5$，我们能够在$4$处“等待”，但这显然不可能用DFS实现

因为对于$4$号节点来说，入边是不可见的，不可能判断出是否需要“等待”

这时就需要用到我们的工具，拓扑排序

拓扑排序能够实现在到达一个节点之间已经遍历过之前的所有节点

最后需要提示的一点

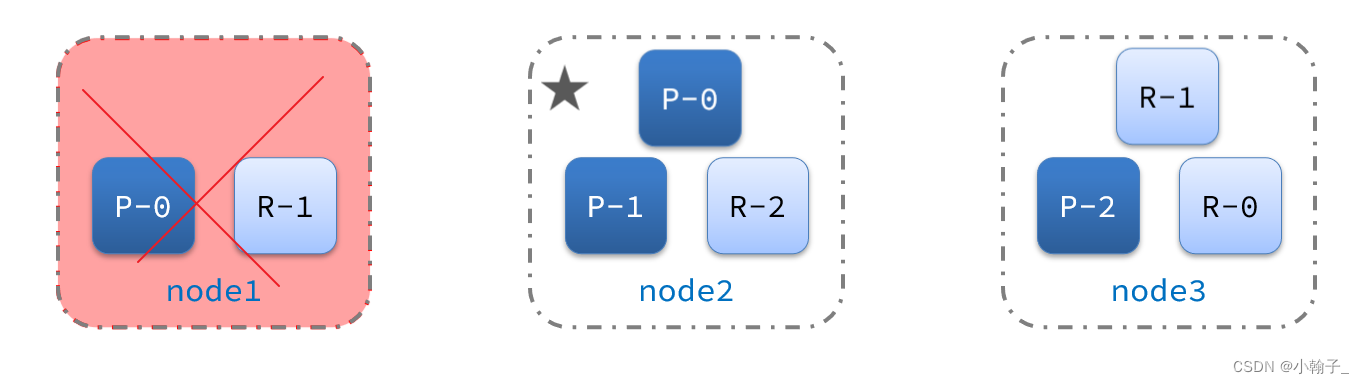
试着考虑图中矩形节点（矩形节点到节点1只有单向边）

这两个节点会影响答案的正确性，因为在拓扑排序 + DP的时候，我们会根据它们的信息更新节点1

解决方法就是在建新图的时候注意将其去除即可（具体如何去除见代码）

Code:

#include <iostream>
#include <string.h>
#include <queue>
using namespace std;
const int max_n = 1e5;
const int max_m = 5e5;
const int max_value = 100;
const int NaN = 0x3F3F3F3F;

int n, m, x, y, z;
struct edge { int v, next; }edges[max_m * 2];
int tot = -1;
int head[max_n + 1];
int value[max_n + 1];
//tarjan
int timeclock = 0, dfn[max_n + 1], low[max_n + 1];
int rsp = -1, stack[max_n + 1], instack[max_n + 1];
int cnt = 0, belong[max_n + 1];
//re_init
edge new_edges[max_m * 2];
int new_head[max_n + 1];
int new_tot = -1;
int invalue[max_n + 1];
int outvalue[max_n + 1];
//topo
int in[max_n + 1];
queue<int>topoq;
//dp
int ans[max_n + 1];


void add_edge(int u, int v) {
	edges[++tot] = { v,head[u] }; head[u] = tot;
}

void add_new_edge(int u, int v) {
	new_edges[++new_tot] = { v,new_head[u] }; new_head[u] = new_tot;
}

void tarjan(int x) {
	dfn[x] = low[x] = ++timeclock;
	stack[++rsp] = x;
	instack[x] = 1;

	for (int i = head[x]; i != -1; i = edges[i].next) {
		int v = edges[i].v;
		if (!dfn[v]) {
			tarjan(v);
			low[x] = min(low[x], low[v]);
		}
		else if (instack[v]) {
			low[x] = min(low[x], low[v]);
		}
	}

	if (dfn[x] == low[x]) {
		cnt++;
		while (stack[rsp + 1] != x) {
			int node = stack[rsp--];
			belong[node] = cnt;
			invalue[cnt] = min(invalue[cnt], value[node]);
			outvalue[cnt] = max(outvalue[cnt], value[node]);
			instack[node] = 0;
		}
	}
}

void re_init() {
	for (int i = 1; i <= n; i++) {
		for (int j = head[i]; j != -1; j = edges[j].next) {
			int v = edges[j].v;
			if (belong[i] && belong[v] && belong[i] != belong[v]) {
                //由于只从1号开始tarjan，从1号不可到达的节点没有归属任何新节点，其belong[x] == 0
				add_new_edge(belong[i], belong[v]);
				in[belong[v]]++;
			}
		}
	}
}

void topo() {
	for (int i = 1; i <= cnt; i++) {
		if (in[i] == 0) {
			topoq.push(i);
		}
	}

	while (!topoq.empty()) {
		int node = topoq.front();
		topoq.pop();
		ans[node] = max(ans[node], outvalue[node] - invalue[node]);

		for (int i = new_head[node]; i != -1; i = new_edges[i].next) {
			int v = new_edges[i].v;
			ans[v] = max(ans[v], ans[node]);//DP
			invalue[v] = min(invalue[v], invalue[node]);//DP
			in[v]--;
			if (!in[v]) topoq.push(v);
		}
	}
}

int main() {
	memset(head + 1, -1, sizeof(int) * max_n);
	memset(new_head + 1, -1, sizeof(int) * max_n);
	memset(invalue + 1, 0x3F, sizeof(int) * max_n);
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> value[i];
	for (int i = 0; i < m; i++) {
		cin >> x >> y >> z;
		add_edge(x, y);
		if (z == 2) add_edge(y, x);
	}

	tarjan(1);//只从1号开始tarjan
	re_init();
	topo();

	cout << ans[belong[n]];
	return 0;
}