题目链接

Leetcode.1590 使数组和能被 P 整除 Rating ： 2039

题目描述

给你一个正整数数组 nums，请你移除 最短 子数组（可以为 空），使得剩余元素的 和 能被 p整除。 不允许 将整个数组都移除。

请你返回你需要移除的最短子数组的长度，如果无法满足题目要求，返回 -1。

子数组 定义为原数组中连续的一组元素。

示例 1：

输入：nums = [3,1,4,2], p = 6
输出：1
解释：nums 中元素和为 10，不能被 p 整除。我们可以移除子数组 [4] ，剩余元素的和为 6 。

示例 2：

输入：nums = [6,3,5,2], p = 9
输出：2
解释：我们无法移除任何一个元素使得和被 9 整除，最优方案是移除子数组 [5,2] ，剩余元素为 [6,3]，和为 9 。

示例 3：

输入：nums = [1,2,3], p = 3
输出：0
解释：和恰好为 6 ，已经能被 3 整除了。所以我们不需要移除任何元素。

示例 4：

输入：nums = [1,2,3], p = 7
输出：-1
解释：没有任何方案使得移除子数组后剩余元素的和被 7 整除。

示例 5：

输入：nums = [1000000000,1000000000,1000000000], p = 3
输出：0

提示：

• $1\le nums.length\le 10^5$
• $1\le nums[i]\le 10^9$
• $1\le p\le 10^9$

分析：前缀和 + 哈希表

我们分析如下例子，nums = [7,3,6,2,5,6,2] , p = 10：

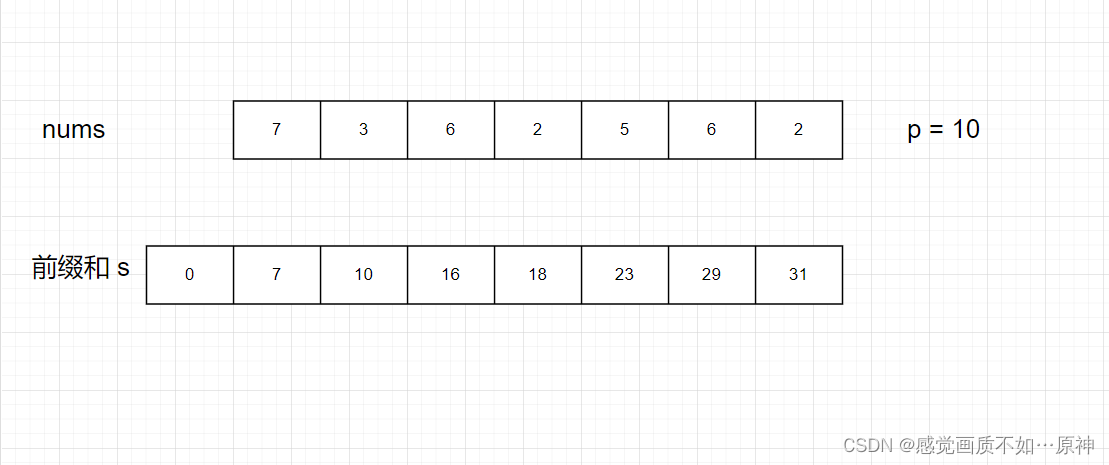
我们注意到，整个数组的和为 31，与 p = 10的余数 r = 1。

要让去掉一个 子数组 之后，剩下元素和是 p的倍数，那么这个被删除的 子数组的和sum与 p的余数也应该是 r。

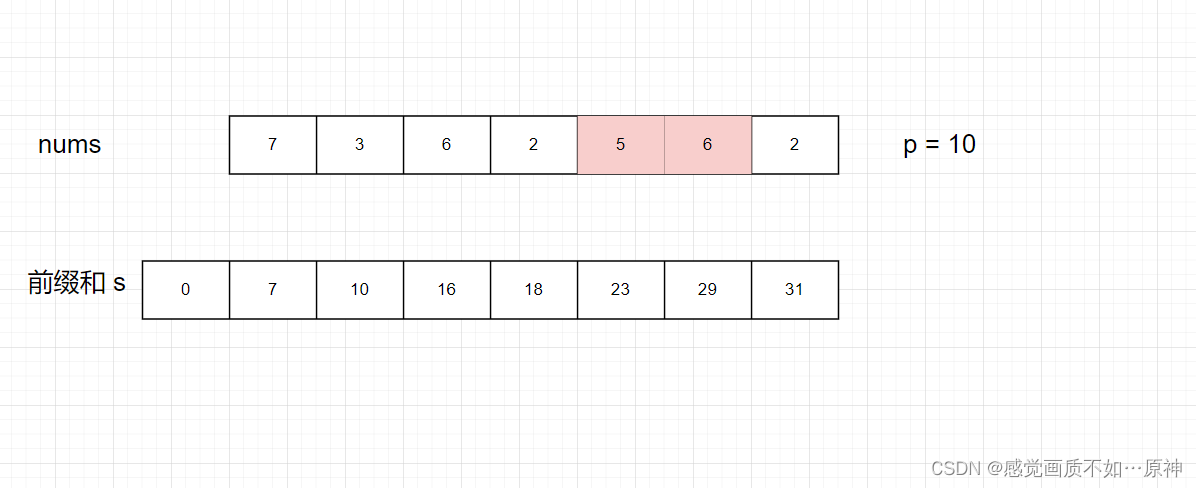
比如，删除 [5,6]，剩下的元素和为 20，正好可以整除 p。

所以，我们的目的就是，找出这样的最短的一段 [ i , j ]，使得 (s[j] - s[i]) % p == r，即找出最短的一个子数组，该子数组的和 sum，让它和 p的余数 为r。

我们可以将 (s[j] - s[i]) % p == r稍微变形，(s[i] % p) == (s[j] - r + p) % p。s[j] - r + p是为了防止 s[j] - r变成负数。

我们用哈希表 m记录 s[j] % p上一次出现的位置 i。

如果哈希表中存在 s[j] % p，说明 (s[j] - s[i]) % p == r，就找到了这样的一个子数组，子数组的长度为 j - i，我们只需要记录最短的那个长度 返回即可。

时间复杂度：$O(n)$

C++代码：

class Solution {
public:
    int minSubarray(vector<int>& nums, int p) {
        int n = nums.size();
        vector<int> s(n+1);

        for(int i = 1;i <= n;i++) s[i] = (s[i-1] + nums[i-1]) % p;

        int r = s[n];

        int ans = n;

        unordered_map<int,int> m;

        for(int j = 0;j <= n;j++){
            m[s[j]] = j;
            if(m.count((s[j] - r + p) % p)){
                int i = m[(s[j] - r + p) % p];
                ans = min(ans,j - i);
            }
        }
        return ans == n ? -1 : ans;
    }
};

Python代码：

class Solution:
    def minSubarray(self, nums: List[int], p: int) -> int:
        s = list(accumulate(nums,initial = 0))
        r = s[-1] % p
        
        n = len(nums)
        ans = n

        m = {}
        for j,sum in enumerate(s):
            m[sum % p] = j
            i = m.get((sum - r) % p,-n)
            ans = min(ans,j - i)

        return ans if ans != n else -1