不同路径

中等

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

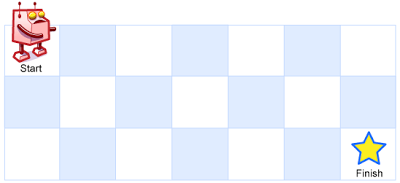
输入：m = 3, n = 7

输出：28

示例 2：

输入：m = 3, n = 2

输出：3

解释：

从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下

2. 向下 -> 向下 -> 向右

3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3

输出：28

示例 4：

输入：m = 3, n = 3

输出：6

题解

1. 因为只能向右或向下走，所以第一行第一列走的位置只能是一，初始化值为1

2. 从(1,1)开始可以从(0,1)(1,0)到达就有两种走法，有dp[i-1][j]+dp[i][j-1]个走法这是规律(可以自己在3x3的格子里写一下试试)

3. 双循环遍历从1开始，就可以求出整个表从开头到结束的走法

class Solution {
    public int uniquePaths(int m, int n) {
        int dp[][] = new int[m][n];
        for(int i = 0;i < m;i++){
            dp[i][0] = 1;
        } 
        for(int j = 0;j < n;j++){
            dp[0][j] = 1;
        } 
        for(int i = 1;i < m;i++){
            for(int j = 1;j < n;j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}