opencv-图像几何处理

news2024/11/15 3:44:59

缩放

缩放只是调整图像的大小。为此，opencv提供了一个cv2.resize()函数，可以手动指定图像大小，也可以指定缩放因子。你可以使用任意一种方法调整图像的大小：

import cv2
from matplotlib import pyplot as plt

logo = cv2.imread('logo.png')
logo_mini = cv2.resize(logo, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_CUBIC)
# 或者这样
# height, width = logo.shape[:2]
# logo_mini = cv2.resize(logo, (int(0.5 * height), int(0.5 * width)), interpolation=cv2.INTER_CUBIC)

plt.subplot(121),plt.imshow(logo, 'gray'),plt.title('logo')
plt.subplot(122),plt.imshow(logo_mini, 'gray'),plt.title('logo_mini')
plt.show()

效果如下：

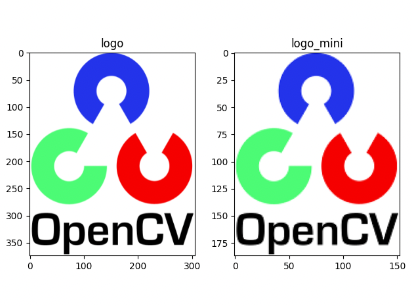
请看logo_mini的宽高与原图缩小了一半！resize(src, dsize, dst=None, fx=None, fy=None, interpolation=None)参数详解如下：

src: 输入图像
dsize: 修改后的图片宽高
dst: 输出图像
fx: 比例因子(宽度)，0.5表示宽度缩放成原来的一半
fy: 比例因子(高度)，0.5表示高度缩放成原来的一半
interpolation: 插值法

平移

平移是物体位置的移动。如果您知道 (x, y) 方向的偏移，让它成为(tx, ty)，M你可以按如下方式创建变换矩阵:

M = [[1, 0, tx], [0, 1, ty]]

你可以把它变成一个np类型的Numpy数组。np.float32()传递到cv2.warpAffine()函数，请看下面栗子：

import cv2
import numpy as np
from matplotlib import pyplot as plt

logo = cv2.imread('logo.png')
rows, cols = logo.shape[:2]
# 水平向右平移50个像素，垂直向下平移100个像素
M = np.float32([[1, 0, 50], [0, 1, 100]])
dst = cv2.warpAffine(logo, M, (cols, rows))
plt.subplot(121),plt.imshow(logo, 'gray'),plt.title('logo')
plt.subplot(122),plt.imshow(dst, 'gray'),plt.title('dst')
plt.show()

效果如下:

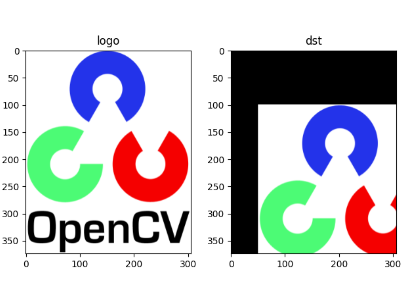
从效果图可以看到，图片水平向右移动了50个像素，垂直向下移动了100个像素。warpAffine(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)参数详解如下:

src: 输入图像
M: 2X3的变换矩阵
dsize: 指定图像输出尺寸
dst: 输出图像
flags: 插值算法标识符

旋转

旋转跟平移一样，同样是通过cv2.warpAffine()函数来实现的。在上面我们知道这个函数接收一个变换矩阵，为了得到这个变换矩阵，OpenCV 提供了一个函数cv2.getRotationMatrix2D()。下面我们来实现，将logo图像以中心点为圆心，逆时针旋转90度，代码如下：

import cv2
import numpy as np
from matplotlib import pyplot as plt

logo = cv2.imread('logo.png')
rows, cols = logo.shape[:2]
M = cv2.getRotationMatrix2D((int(cols / 2), int(rows / 2)), 90, 1)
dst = cv2.warpAffine(logo, M, (cols, rows))
plt.subplot(121),plt.imshow(logo, 'gray'),plt.title('logo')
plt.subplot(122),plt.imshow(dst, 'gray'),plt.title('dst')
plt.show()

效果如下:

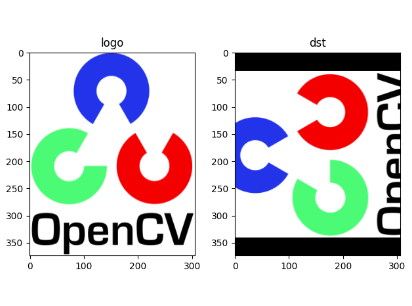
从效果图可以看到，图片围绕中心点逆时针旋转了90度。getRotationMatrix2D(center, angle, scale)参数详解如下:

center: 旋转的中心点
angle: 旋转角度，正数为逆时针，负数为顺时针
scale: 缩放因子

仿射变换

在仿射变换中，原始图像中的所有平行线在输出图像中仍将平行。为了找到变换矩阵，我们需要输入图像中的三个点及其在输出图像中的对应位置。我们可以使用cv2.getAffineTransform()函数将创建一个2*3矩阵，该矩阵将传递给cv2.warpAffine()函数，使用如下：

import cv2
import numpy as np
from matplotlib import pyplot as plt

qipan = cv2.imread('qipan.png')
# 在棋盘中描三个点
cv2.circle(qipan, (103, 103), 5, (255, 0, 0), -1)
cv2.circle(qipan, (103, 196), 5, (255, 0, 0), -1)
cv2.circle(qipan, (196, 103), 5, (255, 0, 0), -1)
rows, cols = qipan.shape[:2]
pts1 = np.float32([[103, 103], [103, 196], [196, 103]])
pts2 = np.float32([[30, 120],[200, 50],[80, 220]])
M = cv2.getAffineTransform(pts1, pts2)
dst = cv2.warpAffine(qipan, M, (rows, cols))
plt.subplot(121),plt.imshow(qipan, 'gray'),plt.title('qipan')
plt.subplot(122),plt.imshow(dst, 'gray'),plt.title('dst')
plt.show()

效果如下:

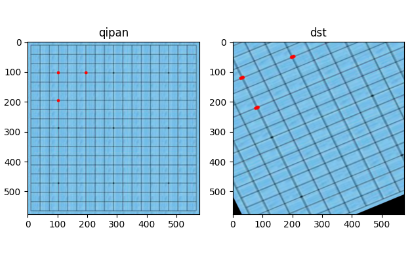
从效果图可以看到，原始图像中的所有平行线在输出图像中仍然平行。getAffineTransform(src, dst)参数详解如下:

src: 输入图像的三个点坐标
dst: 输出图像的三个点坐标

透视变换

对于透视变换，你需要一个3*3变换矩阵，即使在变换之后，直线仍将保持笔直。要找到这个变换矩阵，你需要输入图像上的4个点和输出图像上对应的点。我们可以通过函数cv2.getPerspectiveTransform()找到变换矩阵，然后再将这个变换矩阵应用到cv2.warpPerspective()函数当中，使用如下：

import cv2
import numpy as np
from matplotlib import pyplot as plt

qipan = cv2.imread('qipan-1.png')
pst1 = [[88, 30], [812, 30], [37, 848], [900, 832]]
pst2 = [[0, 0], [500, 0], [0, 500], [500, 500]]
# 在原图上绘制4个点
cv2.circle(qipan, pst1[0], 5, (255, 0, 0), -1)
cv2.circle(qipan, pst1[1], 5, (255, 0, 0), -1)
cv2.circle(qipan, pst1[2], 5, (255, 0, 0), -1)
cv2.circle(qipan, pst1[3], 5, (255, 0, 0), -1)
# 获取变换矩阵
M = cv2.getPerspectiveTransform(np.float32(pst1), np.float32(pst2))
# 透视变换
dst = cv2.warpPerspective(qipan, M, (500, 500))
# 在输出图像中再绘制4个点
cv2.circle(dst, pst2[0], 5, (255, 0, 0), -1)
cv2.circle(dst, pst2[1], 5, (255, 0, 0), -1)
cv2.circle(dst, pst2[2], 5, (255, 0, 0), -1)
cv2.circle(dst, pst2[3], 5, (255, 0, 0), -1)
plt.subplot(121),plt.imshow(qipan, 'gray'),plt.title('qipan')
plt.subplot(122),plt.imshow(dst, 'gray'),plt.title('dst')
plt.show()