视频地址:https://www.bilibili.com/video/BV1uA411N7c5
1. 贪心算法
贪心算法(又称贪婪算法),是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑 —— 所做出的是在某种意义上的局部最优解。
贪心算法并不保证会得到最优解,但是在某些问题上贪心算法的解就是最优解。要会判断一个问题能否用贪心算法来计算。
1.1 找零问题
假设商店老板需要找零n元钱,钱币的面额有:100元、50元、20元、5元、1元,如何找零使得所需钱币的数量最少?
只考虑元,不考虑角和分
def chaneg(t, n):
"""
t: 钱的面额
n: 需要找零的金额
"""
m = [0 for _ in range(len(t))] # t对应的使用次数
for i, money in enumerate(t):
m[i] = n // money # 对应面额的数量
n = n % money # 还剩下的钱
else: # n表示剩下没找开的钱
return m, n
if __name__ == "__main__":
t = [100, 50, 20, 5, 1]
print(chaneg(t, 376)) # ([3, 1, 1, 1, 1], 0)
print(chaneg(t, 376.5)) # ([3.0, 1.0, 1.0, 1.0, 1.0], 0.5)
1.2 背包问题
一个小偷在某个商店发现 n n n 个商品,第 i i i 个商品价值 v i v_i vi 元,重 w i w_i wi 千克。他希望拿走的价值尽量高,但他的背包最多只能容纳 W W W 千克的东西。他应该拿走哪些商品?
背包问题再往下细分,还有两种问题:
问题1:0-1背包:对于一个商品,小偷要么把它完整拿走,要么留下。不能只拿走一部分,或把一个商品拿走多次。(商品为金条)
问题2:分数背包:对于一个商品,小偷可以拿走其中任意一部分。(商品为金沙)
举例:
- 商品1(金): v 1 = 60 , w 1 = 10 v_1 = 60, w_1 = 10 v1=60,w1=10
- 商品2(银): v 2 = 100 , w 2 = 20 v_2 = 100, w_2 = 20 v2=100,w2=20
- 商品3(铜): v 3 = 120 , w 3 = 30 v_3 = 120, w_3 = 30 v3=120,w3=30
- 背包容量: W = 50 W=50 W=50
对于 0-1背包 和 分数背包,贪心算法是否都能得到最优解?为什么?
思路:先算一下三种商品的 价值/重量,先装最贵的。
对于0-1背包:
- 商品1(金): v 1 = 60 , w 1 = 10 v_1 = 60, w_1 = 10 v1=60,w1=10, 单价:6
- 商品2(银): v 2 = 100 , w 2 = 20 v_2 = 100, w_2 = 20 v2=100,w2=20, 单价:5
- 商品3(铜): v 3 = 120 , w 3 = 30 v_3 = 120, w_3 = 30 v3=120,w3=30, 单价:4
- 背包容量: W = 50 W=50 W=50
所以先拿商品1,再拿商品2,此时拿不走商品3了,此时总价值160,并不是最优解。所以 0-1背包 不能用贪心算法来解决。
对于分数背包:
先拿商品1,再拿商品2,最后拿部分的商品3。
def fractional_backpack(goods, vol):
"""
goods: 商品 (价格, 重量)
vol: 背包容量
"""
# 确定返回值
strategy = [0 for _ in range(len(goods))] # 对应的是排好序的goods
# 拿走商品的总价值
total_value = 0
for i, (price, weight) in enumerate(goods):
if vol >= weight:
strategy[i] = 1
# 更新vol
vol -= weight
total_value += price
else:
strategy[i] = vol / weight
# 更新vol
vol = 0
total_value += strategy[i] * price
break
print("Item : Times")
for key, value in dict(zip(goods, strategy)).items():
print(f"{key} : {value}")
print(f"Total Value: {total_value}")
return strategy, total_value
if __name__ == "__main__":
goods = [(60, 10), (120, 30), (100, 20)]
# 先对good进行排序 -> 按照商品单位重量价值进行降序排序
goods.sort(key=lambda x: x[0] / x[1], reverse=True)
fractional_backpack(goods, 50)
"""
Item : Times
(60, 10) : 1
(100, 20) : 1
(120, 30) : 0.6666666666666666
Total Value: 240.0
"""
1.3 拼接最大数字问题
有 n n n 个非负整数,将其按照字符串拼接的方式拼接为一个整数,如何拼接可以使得得到的整数最大?
例:32,94,128,1286,6,71可以拼接出的最大整数为94716321286128。
思路:字符串比大小的顺序来进行
小坑:128和1286怎么比?
解决思路:
a = 128
b = 1286
a + b if (a+b) > (b+a) else b + a
解题方法:
from functools import cmp_to_key
def xy_cmp(x, y):
if x + y < y + x:
return 1
elif x + y > y + x:
return -1
else:
return 0
def number_join(ls):
# 先将整数变为字符串
ls = list(map(str, ls)) # ['32', '94', '128', '1286', '6', '71']
# 按照第一个字符串排序
ls.sort(key=cmp_to_key(xy_cmp))
return "".join(ls)
if __name__ == '__main__':
ls = [32, 94, 128, 1286, 6, 71]
print(number_join(ls)) # 94716321286128
1.4 活动选择问题
假设有 n n n 个活动,这些活动要占用同一片场地,而场地在某时刻只能供一个活动使用。每个活动都有一个开始时间 s i s_i si 和结束时间 f i f_i fi (题目中时间以整数表述),表示活动在 [ s i , f i ) [s_i, f_i) [si,fi) 区间占用场地。问:安排哪些活动能够使该场地举办的活动数量最多?

贪心结论:最先结束的活动一定是最优解的一部分。
证明:假设 a a a 是所有活动中最先结束的活动, b b b 是最优解中最先结束的活动。如果 a = b a = b a=b,结论成立;如果 a ≠ b a \neq b a=b,则 b b b 的结束时间一定晚于 a a a 的结束时间,则此时用 a a a 替换掉最优解中的 b b b, a a a 一定不与最优解中的其他活动时间重叠,因此替换后的解也是最优解。
def activity_selection(activities):
res = []
res.append(activities[0]) # 第一个活动是最先结束的活动
for i in range(1, len(activities)):
# 如果下一个活动的开始时间≥上一个活动的结束时间 -> 不冲突
if activities[i][0] >= res[-1][1]: # [0]: 开始时间; [1]: 结束时间
res.append(activities[i])
return res
if __name__ == '__main__':
activities = [(1, 4), (3, 5), (0, 6), (5, 7), (3, 9), (5, 9),
(6, 10), (8, 11), (8, 12), (2, 14), (12, 16)]
# 保证活动是按照结束时间排好序的
activities.sort(key=lambda x: x[1])
print(activity_selection(activities)) # [(1, 4), (5, 7), (8, 11), (12, 16)]
2. 动态规划 (Dynamic Programming)
[概况]:动态规划(Dynamic Programming, DP)是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划的应用极其广泛,包括工程技术、经济、工业生产、军事以及自动化控制等领域,并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。
[原理]:动态规划问世以来,在经济管理、生产调度、工程技术和最优控制等方面得到了广泛的应用。例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题,用动态规划方法比用其它方法求解更为方便。
虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
[概念引入]:在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若干个互相联系的阶段,在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定,它依赖于当前面临的状态,又影响以后的发展。当各个阶段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线.这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程,这种问题称为多阶段决策问题。在多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义,称这种解决多阶段决策最优化的过程为动态规划方法。
[基本思想]:动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
动态规划不是一种特定的算法,而是一种算法思想。
2.1 从斐波那契数列看动态规划
- 斐波那契数列: F 1 = 1 , F 2 = 2 F_1 = 1, F_2 = 2 F1=1,F2=2, F n = F n − 1 + F n − 2 F_n = F_{n-1} + F_{n -2} Fn=Fn−1+Fn−2
- 练习:使用递归和非递归的方法来求解斐波那契数列的第 n n n 项。
from cal_time import cal_fn_time
def fibnacci(n):
if n == 1 or n == 2:
return 1
else:
return fibnacci(n - 1) + fibnacci(n - 2)
@cal_fn_time
def fibnacci_time(*args, **kwargs):
return fibnacci(*args, **kwargs)
@cal_fn_time
def fibnacci_no_recurision(n):
f = [0, 1, 1]
if n > 2:
for i in range(n - 2):
num = f[-1] + f[-2]
f.append(num)
return f[n]
if __name__ == '__main__':
print(fibnacci_time(5)) # 5 0.0000 ms
print(fibnacci_time(10)) # 55 0.0000 ms
print(fibnacci_time(20)) # 6765 3.0372 ms
print(fibnacci_time(30)) # 832040 243.0727 ms
print("----------")
print(fibnacci_no_recurision(5)) # 5 0.0000 ms
print(fibnacci_no_recurision(10)) # 55 0.0000 ms
print(fibnacci_no_recurision(20)) # 6765 0.0000 ms
print(fibnacci_no_recurision(30)) # 832040 0.0000 ms
print(fibnacci_no_recurision(50)) # 12586269025 0.0000 ms
可以看到,使用递归的fibnacci数列求解非常慢。这是因为递归有子问题的重复计算,比如说求 F ( 5 ) F(5) F(5) 时会用到 F ( 4 ) F(4) F(4) 和 F ( 3 ) F(3) F(3),而求 F ( 4 ) F(4) F(4) 的时候会用到 F ( 3 ) F(3) F(3) 和 F ( 2 ) F(2) F(2),那么 F ( 3 ) F(3) F(3) 就被重复计算了(算了两次)。
而使用非递归的算法时,因此计算结果都存在list中,因此不会出现子问题重复计算的问题。而这种非递归的思想,就是动态规划的思想。
动态规划的两个重点:
- 最优子结构:要想解决这个问题,解决它的子问题就好:递归式(如Fabnacci)
- 重复子问题:把重复计算的结构存起来
2.2 钢条切割问题
某公司出售钢条,出售价格与钢条长度之间的关系如下表:

问题:现在有一段长度为 n n n 的钢条和上面的价格表,求切割钢条方案,使得总收益最大。
长度为4的钢条的所有切割方案如下:(c方案为最优)

思考:长度为 n n n 的钢条的不同切割方案有几种?
答: 2 n − 1 2^{n-1} 2n−1种方案。
一根钢条有 n − 1 n-1 n−1 个切割点,每个切割点都有切和不切两种方案,所以是 2 n − 1 2^{n-1} 2n−1种切割方案。

r[i]是最优的收益。
当我们求出前面的,后面的最优解就可以直接用前面的来得出了。
2.2.1 递推式
设长度为 n n n 的钢条切割后最优收益值为 r n r_n rn,可以得出递推式:
r n = max ( p n , r 1 + r n − 1 , r 2 + r n − 2 , . . . , r n − 1 + r 1 ) r_n = \max(p_n, r_1 + r_{n - 1}, r_2 + r_{n - 2}, ..., r_{n - 1} + r_1) rn=max(pn,r1+rn−1,r2+rn−2,...,rn−1+r1)
- 第一个参数
p
n
p_n
pn 表示不切割,其他
n
−
1
n-1
n−1 个参数分别表示另外
n
−
1
n - 1
n−1种不同切割方案,对于方案
i
=
1
,
2
,
.
.
.
,
n
−
1
i=1, 2, ..., n - 1
i=1,2,...,n−1:
- 将钢条切割为长度为 i i i 和 n − i n - i n−i 两段
- 方案 i i i 的收益为切割两段的最优收益之和
- 考察所有的 i i i,选择其中收益最大的方案
代码如下:
def cut_rod_recursion_1(p, n):
"""
p: 钢条的价格, 其索引就是该价格下的长度
n: 钢条的长度
$$
r_n = \max(p_n, r_1 + r_{n - 1}, r_2 + r_{n - 2}, ..., r_{n - 1} + r_1)
$$
"""
if n == 0:
return 0
else:
res = p[n] # 不切割的收益
for i in range(1, n): # 1, n-1
res = max(res, cut_rod_recursion_1(p, i) + cut_rod_recursion_1(p, n - i))
return res
2.2.2 最优子结构
可以将求解规模为 n n n 的原问题,划分为规模更小的子问题:完成一次切割后,可以将产生的两段钢条看成两个独立的钢条切割问题。
组合两个子问题的最优解,并在所有可能的两段切割方案中选取组合收益最大的,构成原问题的最优解。
钢条切割满足最优子结构:问题的最优解由相关子问题的最优解组合而成,这些子问题可以独立求解。
钢条切割问题还存在更简单的递归求解方法:
- 从钢条的左边切割下长度为 i i i 的一段,只对右边剩下的一段继续进行切割,左边的不再切割
- 递推式简化为: r n = max 1 ≤ i ≤ n ( p i + r n − 1 ) r_n = \underset{1\le i \le n}{\max}(p_i + r_{n - 1}) rn=1≤i≤nmax(pi+rn−1)
- 不做切割的方案就可以描述为:左边一段长度为 n n n,收益为 p n p_n pn,剩余一段长度为0,收益为 r 0 = 0 r_0 = 0 r0=0。
代码如下:
def cut_rod_recursion_2(p, n):
"""
$r_n = \\underset{1\le i \le n}{\max}(p_i + r_{n - 1})$
"""
if n == 0:
return 0
else:
res = 0
for i in range(1, n + 1):
res = max(res, p[i] + cut_rod_recursion_2(p, n - i))
return res
完整代码如下:
import time
def cal_fn_time(fn):
def wrapper(*args, **kwargs):
t1 = time.time()
res = fn(*args, **kwargs)
t2 = time.time()
print(f"{fn.__name__}'s running time is: {(t2 - t1) * 1000:.4f} ms")
return res
return wrapper
def cut_rod_recursion_1(p, n):
"""
p: 钢条的价格, 其索引就是该价格下的长度
n: 钢条的长度
$$
r_n = \max(p_n, r_1 + r_{n - 1}, r_2 + r_{n - 2}, ..., r_{n - 1} + r_1)
$$
"""
if n == 0:
return 0
else:
res = p[n] # 不切割的收益
for i in range(1, n): # 1, n-1
res = max(res, cut_rod_recursion_1(p, i) + cut_rod_recursion_1(p, n - i))
return res
@cal_fn_time
def cut_rod_recursion_1_time(*args, **kwargs):
return cut_rod_recursion_1(*args, **kwargs)
def cut_rod_recursion_2(p, n):
"""
$r_n = \\underset{1\le i \le n}{\max}(p_i + r_{n - 1})$
"""
if n == 0:
return 0
else:
res = 0
for i in range(1, n + 1):
res = max(res, p[i] + cut_rod_recursion_2(p, n - i))
return res
@cal_fn_time
def cut_rod_recursion_2_time(*args, **kwargs):
return cut_rod_recursion_2(*args, **kwargs)
if __name__ == '__main__':
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
p_exp = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]
print(cut_rod_recursion_1(p, 9)) # 25
print(cut_rod_recursion_2(p, 9)) # 25
print(cut_rod_recursion_1_time(p_exp, 15)) # 42 1671.4497 ms
print(cut_rod_recursion_2_time(p_exp, 15)) # 42 12.9933 ms
2.2.3 自顶向下的递归实现
def _cut_rod(p, n):
if n == 0:
return 0
q = 0
for i in range(1, n + 1):
q = max(q, p[i] + _cut_rod(p, n - i))
return q
递归的时候,
n-1说明n一直在减小,所以是从上往下的递归。
为何自顶向下的递归实现的效率会这么差?
- 时间复杂度: O ( 2 n ) O(2^n) O(2n)

可以从图中可以看到,还是存在大量的重复子问题计算,这样就会导致算法的效率很差。
2.3.4 动态规划解法
递归算法由于重复求解相同子问题,效率极低,因此可以使用动态规划的思想来做:
- 每个子问题只求解一次,保存求解的结果
- 之后需要此问题时,只需查找保存的结果
需要自底向上的算
代码如下:
def cir_rod_dynamic_programming(p, n):
"""
使用动态规划的思想来实现自底向上的算
$r_n = \max(p_i + r_{n - 1})$
"""
# 开一个列表用来存放结果
r = [0] # 长度为0时,收益为0
for i in range(1, n + 1): # [1, n+1]
res = 0
for j in range(1, i + 1): # i就相当于是n
res = max(res, p[j] + r[i - j])
r.append(res)
return r[n]

时间复杂度: O ( n 2 ) O(n^2) O(n2)
| 时间复杂度 | |
|---|---|
| 自顶向下 | O ( 2 n ) O(2^{n}) O(2n) |
| 自底向上 | O ( n 2 ) O(n^2) O(n2) |
可以看到,使用了动态规划,算法的时间复杂度大幅度降低!
2.3.4 重构解
如何修改动态规划算法,使其不仅输出最优解,还输出最优切割方案?
对每个子问题,保存切割一次时左边切下的长度:

s [ i ] s[i] s[i]是用来记录左边切割的长度
- 对于 i = 4 i=4 i=4, s [ i ] = 2 s[i] = 2 s[i]=2,说明 4 = 2 + 2 4 = 2 + 2 4=2+2,2的价值已经知道了;
- 对于 i = 5 i=5 i=5, s [ i ] = 2 s[i] = 2 s[i]=2,说明 5 = 2 + 3 5 = 2 + 3 5=2+3,2的价值已经知道了,3的最优价值也知道了,所以总价值=5+8=13;
- 对于 i = 9 i=9 i=9, s [ i ] = 3 s[i] = 3 s[i]=3,说明 9 = 2 + 7 9 = 2 + 7 9=2+7,2的价值已经知道了;7的 s [ i ] = 1 s[i]=1 s[i]=1,所以 7 = 1 + 6 7 = 1 + 6 7=1+6,以此类推…
def cut_rod_dp(p, n):
# 开一个列表用来存放结果
r = [0] # 长度为0时,收益也为0
for i in range(1, n + 1):
res = 0
for j in range(1, i + 1): # i就相当于是n
res = max(res, p[j] + r[i - j])
r.append(res)
return r[n]
def cut_rod_extend(p, n): # 重构解
r = [0]
s = [0]
for i in range(1, n + 1): # 从底向上算
res_r = 0 # 记录最优价值
res_s = 0 # 记录最优左边长度
for j in range(1, i + 1):
if p[j] + r[i - j] > res_r:
res_r = p[j] + r[i - j]
res_s = j
r.append(res_r)
s.append(res_s)
return r[n], s
def cut_rod_solution(p, n):
r, s = cut_rod_extend(p, n) # 最优值和s表得到了
solution = []
while n > 0:
solution.append(s[n]) # 先把左边的加进去
n -= s[n]
return solution
if __name__ == '__main__':
p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
p_exp = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]
print(cut_rod_dp(p, 10))
r, s = cut_rod_extend(p, 10)
print(s)
print(f"Price: {cut_rod_extend(p, 10)}, solution: {cut_rod_solution(p, 10)}")
# Price: (30, [0, 1, 2, 3, 2, 2, 6, 1, 2, 3, 10]), solution: [10]
print(f"Price: {cut_rod_extend(p, 9)}, solution: {cut_rod_solution(p, 9)}") # [1, 6]
# Price: (25, [0, 1, 2, 3, 2, 2, 6, 1, 2, 3]), solution: [3, 6]
print(f"Price: {cut_rod_extend(p, 8)}, solution: {cut_rod_solution(p, 8)}") # [1, 6]
# Price: (22, [0, 1, 2, 3, 2, 2, 6, 1, 2]), solution: [2, 6]
2.3 动态规划问题关键特征
什么问题可以使用动态规划方法?
- 有最优值的问题可以考虑使用动态规划
- 最优子结构
- 原问题的最优解中涉及多少个子问题
- 在确定最优解使用哪些子问题时,需要考虑多少种选择
- 重叠子问题(为避免重复计算,动态规划是一种很好的方法)
递推式在解决实际问题时,是很难找的😂
2.4 最长公共子序列
一个序列的子序列是在该序列中删去若干元素后得到的序列。例:"ABCD"和"BDF"都是"ABCDEFG"的子序列。
最长公共子序列(LCS)问题:给定两个序列X和Y,求X和Y长度最大的公共子序列。例:X="ABBCBDE",Y="DBBCDB",LCS(X, Y)="BBCD"
注意:这里并不是说LCS必须是连着的!
应用场景:长公共子序列是一个十分实用的问题,它可以描述两段文字之间的“相似度”,即它们的雷同程度,从而能够用来辨别抄袭。对一段文字进行修改之后,计算改动前后文字的最长公共子序列,将除此子序列外的部分提取出来,这种方法判断修改的部分,往往十分准确。简而言之,百度知道、百度百科都用得上。
字符串相似度比对
一个字符串的子串有 2 n 2^n 2n个(包含空序列,空序列是任意一个序列的子序列)。
这道题是求最长的公共子序列,因此是一个求最优的问题,我们就要思考是否可以用动态规划的思想来做,因此需要思考。
思考:
- 暴力穷举法的时间复杂度是多少?
- 最长公共子序列是否具有最优子结构性质?
2.4.1 定理
定理(LCS的最优子结构):令 X = < x 1 , x 2 , . . . , x m > X=<x_1, x_2, ..., x_m> X=<x1,x2,...,xm> 和 Y = < y 1 , y 2 , . . . , y n > Y=<y_1, y_2, ..., y_n> Y=<y1,y2,...,yn> 为两个序列, Z = < z 1 , z 2 , . . . , z k > Z=<z_1, z_2, ..., z_k> Z=<z1,z2,...,zk> 为 X X X 和 Y Y Y 的任意LCS。
- 如果 x m = y n x_m = y_n xm=yn,则 z k = x m = y n z_k = x_m = y_n zk=xm=yn 且 Z k − 1 Z_{k-1} Zk−1 是 X m − 1 X_{m - 1} Xm−1 和 Y n − 1 Y_{n-1} Yn−1 的一个LCS。
- 如果 x m ≠ y n x_m \ne y_n xm=yn,那么 z k ≠ x m z_k \ne x_m zk=xm 且 意味着 Z Z Z 是 X m − 1 X_{m - 1} Xm−1 和 Y Y Y 的一个LCS。
- 如果 x m ≠ y n x_m \ne y_n xm=yn,那么 z k ≠ y n z_k \ne y_n zk=yn 且 意味着 Z Z Z 是 X X X 和 Y n − 1 Y_{n - 1} Yn−1 的一个LCS。
对于1:假设 X = <A, B, C, D>, Y=<A, B, D>,它们的LCS是 <ABD>,那么就可以说 <A, B, C> 和 <A, B> 的LCS是 <A, B>。意思就是说,如果两个字符的最后一个字符相等,那么两者同时扔掉这个相同的字符,LCS也需要扔掉这个字符。
也可以用长度来理解,X的长度是
m
m
m,Y的长度是
n
n
n,它们的LCS长度是
k
k
k。如果它们最后一个字符相等的话,去掉这个相等的字符,X的长度变为
m
−
1
m-1
m−1,Y的长度变为
n
−
1
n-1
n−1,LCS的长度变为
k
−
1
k-1
k−1。
对于2和3:假设 X = <A, B, C, D>, Y=<A, B, C>,这两个字符长的最后一个字符不相等,那么LCS的长度等于X = <A, B, C>和Y=<A, B, C>的LCS的长度 或者 等于X = <A, B, C, D>和Y=<A, B>的LCS的长度,这两个取最大值。
例子:要求a="ABCBDAB"与b="BDCABA"的LCS。
因为两个字符串的最后一个字符不同("B" ≠ "A"),因此LCS(a, b)应该来源于LCS(a[: -1], b)与LCS(a, b[: -1])中更大的那一个。
因为两个字符串最后一位不相同,因此对于两个字符串而言,二者中的最后一位要想是LCS的一部分,就必须不能同时是两个字符串的最后一位。这意味着对于字符串X而言,LCS要想保留
X[-1],那么Y就必须不能保留Y[-1];对于Y也是同理。
2.4.2 最优解推导式
最优解的推导式如下:

灰色的表示LCS的具体字符串内容
c [ i , j ] = { 0 若 i = 0 或 j = 0 c [ i − 1 , j − 1 ] + 1 若 i , j > 0 且 x i = y i max ( c [ i , j − 1 ] , c [ i − 1 , j ] ) 若 i , j > 0 且 x i ≠ y i c[i, j] = \begin{cases} 0 & 若 i = 0 或 j = 0 \\ c[i - 1, j - 1] + 1 & 若i,j > 0且x_i = y_i \\ \max(c[i, j-1], c[i-1,j]) & 若i,j > 0 且 x_i \ne y_i \end{cases} c[i,j]=⎩ ⎨ ⎧0c[i−1,j−1]+1max(c[i,j−1],c[i−1,j])若i=0或j=0若i,j>0且xi=yi若i,j>0且xi=yi
其中, c [ i , j ] c[i, j] c[i,j] 表示 X i X_i Xi 和 Y j Y_j Yj 的LCS长度。
最终我们求的是 c [ 7 , 6 ] c[7, 6] c[7,6]就是LCS的长度。
第一行:都是空串,所以都是0
第二行:如果两个字符串的最后一个字符相等,那么都-1的LCS+1,即左上方的数值+1
第三行:因为两个字符串的最后一个字符不相等,因此两个字符串分别-1,再取二者的最大值,即取Max(上方, 左方)
举个例子:CA和CB,A ≠ B,因此LCS来自于
max
(
[
C
A
,
C
]
L
C
S
,
[
C
B
,
C
]
L
C
S
)
\max([CA, C]_{\rm LCS}, [CB, C]_{\rm LCS})
max([CA,C]LCS,[CB,C]LCS)。
再举个例子:CA和AB,A 不等于 B,因此LCS来自于
max
(
[
C
A
,
A
]
L
C
S
,
[
A
B
,
C
]
L
C
S
)
\max([CA, A]_{\rm LCS}, [AB, C]_{\rm LCS})
max([CA,A]LCS,[AB,C]LCS)。
创建那个表的时候,i=0和j=0都是默认的,我们一行一行的填。对于 i=1, j=1而言,左右和左上都有数,因此是可以填的,一行一行的,我们就都可以填完了!
2.4.3 LCS长度的代码实现
代码实现:
def lcs_length(x, y):
"""
x: 字符串X
y: 字符串Y
"""
m = len(x) # x的字符串长度
n = len(y) # y的字符串长度
# 因为i=0和j=0并不在两个字符串长度范围内,因此需要再扩充一行一列
c = [[0 for _ in range(n + 1)] for _ in range(m + 1)] # m+1行, n+1列
"""
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
"""
# 一行一行的填充值(因为我们扩充了一行一列,而一行一列我们不考虑,因此是[1, m]和[1, n])
for i in range(1, m + 1): # [1, m]
for j in range(1, n + 1): # [1, n]
# 因为i和j都是大于0的,所以我们不考虑(而且前面定义的c的时候也都赋0了)
"""
虽然公式是x[i] == y[j],但是我们的i和j都是从1开始的,
对应字符串应该是从0开始,所以需要-1
意思就是,字符串x和y的索引应该-1,而c的索引是不需要-1的!
i-1和j-1对于x和y而言不会越界,因为i和j最小值为1,
同理,对c也不会越界
"""
if x[i - 1] == y[j - 1]: # i和j位置上的字符相等,看左上方的+1
c[i][j] = c[i - 1][j - 1] + 1
else:
c[i][j] = max(c[i - 1][j], c[i][j - 1])
# 打印一下填充后的二维列表
for _ in c:
print(_)
return c[m][n]
if __name__ == "__main__":
x = "ABCBDAB"
y = "BDCABA"
print(lcs_length(x, y))
"""
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 1, 1]
[0, 1, 1, 1, 1, 2, 2]
[0, 1, 1, 2, 2, 2, 2]
[0, 1, 1, 2, 2, 3, 3]
[0, 1, 2, 2, 2, 3, 3]
[0, 1, 2, 2, 3, 3, 4]
[0, 1, 2, 2, 3, 4, 4]
4
"""
2.4.4 LCS具体内容
现在我们只是知道,LCS的长度,但我们还没有确定LCS的具体内容。

我们看这个表可以看到,灰色的表示LCS的具体字符串内容。我们观察发现,当有斜着过来的,表示该行和该列的字母是相等的(匹配的),那我们找的就是匹配的过程,并确定它匹配的位置,这样我们就可以确定LCS的具体内容。
2.4.5 TraceBack回溯法
思路:TraceBack(回溯):从最后一个往回找。
- 最后[7, 6]是4,它的箭头是↑,表示它来自于上方,即[6, 6];
- [6, 6]的箭头是↖,表示来自左上方(来自左上方表示匹配 ->
A),即[5, 5]; - [5, 5]的箭头是 ↑,表示来自上方,即[4, 5];
- [4, 5]的箭头是↖,表示来自左上方(来自左上方表示匹配 ->
B),即[3, 4]; - [3, 4]的箭头是←,表示来自左方,即[3, 3];
- [3, 3]的箭头是↖,表示来自左上方(来自左上方表示匹配 ->
C),即[2, 2]; - [2, 2]的箭头是←,表示来自左方,即[2, 1];
- [2, 1]的箭头是↖,表示来自左上方(来自左上方表示匹配 ->
B),即[1, 0]; - [1, 0]是空串,停止回溯。因此可以确定最终的LCS:
BCBA
TraceBack方法要求我们记录箭头
2.4.6 TraceBack回溯法代码实现
代码实现:
def lcs_length(x, y):
"""
x: 字符串X
y: 字符串Y
"""
m = len(x) # x的字符串长度
n = len(y) # y的字符串长度
# 因为i=0和j=0并不在两个字符串长度范围内,因此需要再扩充一行一列
c = [[0 for _ in range(n + 1)] for _ in range(m + 1)] # m+1行, n+1列
"""
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
"""
# 一行一行的填充值(因为我们扩充了一行一列,而一行一列我们不考虑,因此是[1, m]和[1, n])
for i in range(1, m + 1): # [1, m]
for j in range(1, n + 1): # [1, n]
# 因为i和j都是大于0的,所以我们不考虑(而且前面定义的c的时候也都赋0了)
"""
虽然公式是x[i] == y[j],但是我们的i和j都是从1开始的,
对应字符串应该是从0开始,所以需要-1
意思就是,字符串x和y的索引应该-1,而c的索引是不需要-1的!
i-1和j-1对于x和y而言不会越界,因为i和j最小值为1,
同理,对c也不会越界
"""
if x[i - 1] == y[j - 1]: # i和j位置上的字符相等,看左上方的+1
c[i][j] = c[i - 1][j - 1] + 1
else:
c[i][j] = max(c[i - 1][j], c[i][j - 1])
# 打印一下填充后的二维列表
for _ in c:
print(_)
return c[m][n]
def lcs_record_arrows(x, y):
m = len(x)
n = len(y)
c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
# 定义相同的二维数组,用来记录箭头
# 0: 没有方向(空串); 1: 左上方(↖); 2: 上方(↑); 3: 左方(←)
arrow_ls = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
"""
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0]
"""
for i in range(1, m + 1):
for j in range(1, n + 1):
if x[i - 1] == y[j - 1]: # i和j位置上的字符相等,看左上方的+1
c[i][j] = c[i - 1][j - 1] + 1
arrow_ls[i][j] = 1 # 确定↖
elif c[i - 1][j] >= c[i][j - 1]: # 上方↑ (>=优先上方)
c[i][j] = c[i - 1][j]
arrow_ls[i][j] = 2
else: # 左方←
c[i][j] = c[i][j - 1]
arrow_ls[i][j] = 3
return c[m][n], arrow_ls
def lcs_traceback(x, y):
"""
回溯算法
"""
lcs_len, arrows = lcs_record_arrows(x, y)
# 确定最后一个位置
i = len(x)
j = len(y)
# 存放LCS的具体字符
res = []
# 当i <= 0或 j <= 0时停止
while i > 0 and j > 0: # 否命题是或,则逆命题是与
if arrows[i][j] == 1: # 来自↖:匹配的
res.append(x[i - 1]) # 和之前一样,对于x和y而言,还是要-1的
# 确定下一步怎么走
i -= 1
j -= 1
elif arrows[i][j] == 2: # 来自↑:不匹配的
i -= 1
elif arrows[i][j] == 3: # 来自←:不匹配的
j -= 1
# 因为我们是回溯,所以res是倒着的
res.reverse() # list.reverse()没有返回值!
# "".join(map(str, res))是常见的把list转换为str
return " ".join(map(str, res))
if __name__ == "__main__":
x = "ABCBDAB"
y = "BDCABA"
print(lcs_length(x, y))
print()
"""
[0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 1, 1]
[0, 1, 1, 1, 1, 2, 2]
[0, 1, 1, 2, 2, 2, 2]
[0, 1, 1, 2, 2, 3, 3]
[0, 1, 2, 2, 2, 3, 3]
[0, 1, 2, 2, 3, 3, 4]
[0, 1, 2, 2, 3, 4, 4]
4
"""
lcs_length, arrow_ls = lcs_record_arrows(x, y)
print(lcs_length) # 4
for _ in arrow_ls:
print(_)
print()
"""
[0, 0, 0, 0, 0, 0, 0]
[0, 2, 2, 2, 1, 3, 1]
[0, 1, 3, 3, 2, 1, 3]
[0, 2, 2, 1, 3, 2, 2]
[0, 1, 2, 2, 2, 1, 3]
[0, 2, 1, 2, 2, 2, 2]
[0, 2, 2, 2, 1, 2, 1]
[0, 1, 2, 2, 2, 1, 2]
"""
res = lcs_traceback(x, y)
print(res) # B C B A
3. 欧几里得算法
3.1 最大公约数
约数:如果整数 a a a 能被整数 b b b 整除,那么 a a a 叫做 b b b 的倍数, b b b 叫做 a a a 的约数。
给定两个整数 a , b a, b a,b,两个数的所有公共约数中的最大值即为最大公约数 (Greatest Common Divisor, GCD)。
例子:12与16的最大公约数是4.
如何计算两个数的最大公约数:
- 欧几里得:辗转相除法(欧几里得算法)
- 《九章算术》:更相减损术
这两个算法的本质是一样的,前者是除,后者是减
3.2 欧几里得算法
欧几里得算法的公式如下:
gcd ( a , b ) = gcd ( b , a m o d b ) \gcd(a, b) = \gcd(b, a \ {\rm mod} \ b) gcd(a,b)=gcd(b,a mod b)
mod=%—— 取余数
例子:gcd(60, 21) = gcd(21, 18) = gcd(18, 3) = gcd(3, 0) = 3
代码实现:
def gcd(a, b):
"""
最后的b肯定会变为零,此时a就是最大公约数
"""
if b == 0:
return a
else:
return gcd(b, a % b)
def gcd_no_recursion(a, b):
while b > 0:
tmp = a % b
a = b
b = tmp
return a
if __name__ == "__main__":
print(gcd(12, 16)) # 4
print(gcd_no_recursion(12, 16)) # 4
3.3 应用:实现分数计算
利用欧几里得算法实现一个分数类,支持分数的四则运算。
class Fraction:
def __init__(self, a, b):
"""
a: 分子
b: 分母
"""
self.a = a
self.b = b
# 默认约分
divisor = self.gcd(self.a, self.b)
self.a /= divisor
self.b /= divisor
@staticmethod
def gcd(a, b):
while b > 0:
tmp = a % b
a = b
b = tmp
return a
@staticmethod
def lcm(a, b): # 最小公倍数(least common multiple)
"""
formula:
divisor = gcd(a, b)
(a / divisor) * (b / divisor) * divisor <=> a * b / divisor
"""
divisor = Fraction.gcd(a, b)
return a * b / divisor
def __add__(self, other):
# 两个分子加法,先通分
a = self.a
b = self.b
c = other.a
d = other.b
denominator = self.lcm(b, d) # 分母
# 让分子增加相同的倍数
numerator = a * (denominator / b) + c * (denominator / d)
return Fraction(numerator, denominator)
def __sub__(self, other):
# 两个分子加法,先通分
a = self.a
b = self.b
c = other.a
d = other.b
denominator = self.lcm(b, d) # 分母
# 让分子增加相同的倍数
numerator = a * (denominator / b) - c * (denominator / d)
return Fraction(numerator, denominator)
def __mul__(self, other):
a = self.a
b = self.b
c = other.a
d = other.b
return Fraction(a * c, b * d)
def __truediv__(self, other):
a = self.a
b = self.b
c = other.a
d = other.b
return Fraction(a * d, b * c)
def __str__(self):
return "%d/%d" % (self.a, self.b)
if __name__ == "__main__":
f = Fraction(30, 15)
print(f)
a = Fraction(1, 3)
b = Fraction(1, 2)
print(a + b) # 5/6
print(b - a) # 1/6
print(a * b) # 1/6
print(a / b) # 2/3
4. RSA加密算法
4.1 密码与加密
我们常用的password是口令,和密码不一样
-
传统密码:加密算法是秘密的
- 凯撒密码:每个密码往后移动3位
- 这种密码相对不安全,可以通过暴力枚举破解
-
现代密码系统:加密算法是公开的,秘钥是秘密的
秘钥一般指密钥。 密钥是一种参数,它是在明文转换为密文或将密文转换为明文的算法中输入的参数。密钥分为:
- 对称加密:一个秘钥,可以用来加密也可以用来解密
- 非对称加密:需要两个秘钥,一个用来加密,一个用来解密
4.2 RSA加密算法
RSA非对称加密系统:
- 公钥:用来加密,是公开的
- 私钥:用来解密,是私有的
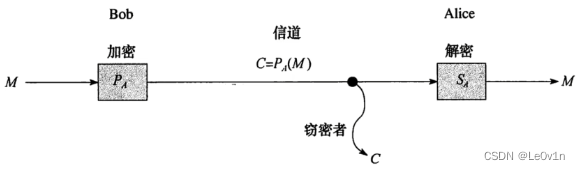
M是明文
加密用的是公钥
C是密文
解密用的是私钥
4.3 RSA加密算法过程
- 随机选取两个质数 p p p和 q q q
- 计算 n = p q n = pq n=pq
- 选取一个与 Φ ( n ) \Phi(n) Φ(n)互质的小奇数 e e e, Φ ( n ) = ( p − 1 ) ( q − 1 ) \Phi(n) = (p - 1)(q - 1) Φ(n)=(p−1)(q−1)
- 对模 Φ ( n ) \Phi(n) Φ(n),计算 e e e的乘法逆元 d d d,即满足 ( e ∗ d ) m o d Φ ( n ) = 1 (e*d) \mod \Phi(n) = 1 (e∗d)modΦ(n)=1
- 公钥 ( e , n ) (e, n) (e,n);私钥 ( d , n ) (d, n) (d,n)
- 加密过程:
c
=
m
e
m
o
d
n
c = m^e \mod n
c=memodn ->
c = m ** e % n - 解密过程:
m
=
c
d
m
o
d
n
m = c^d \mod n
m=cdmodn ->
m = c ** d % n
Q:为什么RAS算法难破解?
A:两个质数算乘法很容易,但是把一个大整数拆成两个质数很难。
15 -> 3 * 5
但对于一个大的整数而言,拆成两个质数的乘积就很难求解。
我们知道公钥 e e e和 n n n,现在想求私钥的 d d d。那么我们需要知道 Φ ( n ) \Phi(n) Φ(n),要想知道 Φ ( n ) \Phi(n) Φ(n),我们就要知道 p p p和 q q q,而 p p p和 q q q是两个质数,二者的乘积等于 n n n,求这两个质数的过程很难。