ccc-pytorch-RNN（7）

news2024/9/27 7:20:08

文章目录

      • 一、RNN简介
      • 二、RNN关键结构
      • 三、RNN的训练方式
      • 四、时间序列预测
      • 五、梯度弥散和梯度爆炸问题

一、RNN简介

RNN（Recurrent Neural Network）中文循环神经网络，用于处理序列数据。它与传统人工神经网络和卷积神经网络的输入和输出相互独立不同，依赖它独特的神经结构（循环核）获得“记忆能力”

注意与递归神经网络(Recursive Neural Network)RNN区分，同时循环神经网络为短期记忆，与（Long Short-Term Memory networks）LSTM的长期记忆不同

二、RNN关键结构

img
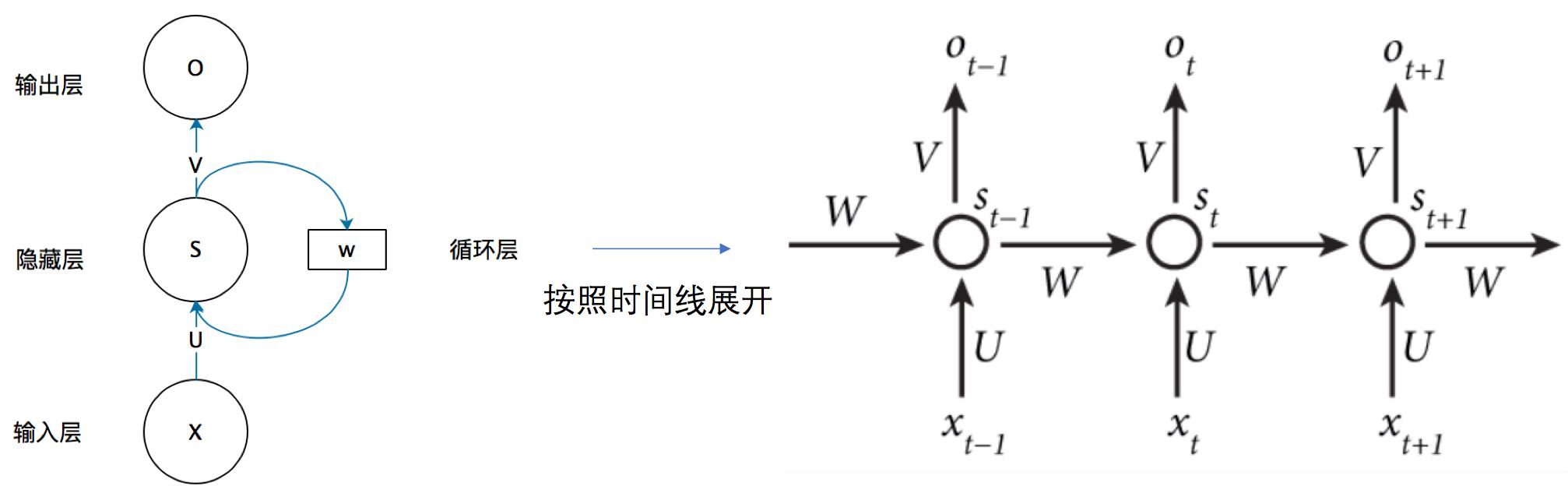
各参数含义：

  • x t x_t xt​：序列t的输入层的值， s t s_t st​：序列t的隐藏层的值 ， o t o_t ot​：序列t的输出层的值
  • U U U：输入层到隐藏层的权重矩阵 ， V V V：隐藏层到输出层的权重矩阵
  • W W W：隐藏层上一次的值作为这一次输入的权重

注意事项：

  • 同不同序列t时的W，V，U相同，即RNN的Weight sharing
  • 结构图中每一步都会有输出，但实际中很可能只需最后一步的输出
  • 为了降低网络复杂度， s t s_t st​只包含前面若干隐藏层的状态

三、RNN的训练方式

本质还是梯度下降的反向传播，由前向传播得到的预测值与真实值构建损失函数，更新W、U、V求解最小值：
S t = f ( U ⋅ X t + W ⋅ S t − 1 + b ) O t = g ( V ⋅ S t ) L t = 1 2 ( Y t − O t ) 2 S_t=f(U\cdot X_t+W\cdot S_{t-1}+b) \\O_t = g(V\cdot S_t) \\ L_t=\frac{1}{2}(Y_t-O_t)^2 St​=f(U⋅Xt​+W⋅St−1​+b)Ot​=g(V⋅St​)Lt​=21​(Yt​−Ot​)2
如果对 t 3 t_3 t3​的U、V、W求偏导如下：

∂ L 3 ∂ V = ∂ L 3 ∂ O 3 ∂ O 3 ∂ V ∂ L 3 ∂ U = ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ∂ S 3 ∂ U + ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ∂ S 3 ∂ S 2 ∂ S 2 ∂ U + ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ∂ S 3 ∂ S 2 ∂ S 2 ∂ S 1 ∂ S 1 ∂ U ∂ L 3 ∂ W = ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ∂ S 3 ∂ W + ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ∂ S 3 ∂ S 2 ∂ S 2 ∂ W + ∂ L 3 ∂ O 3 ∂ O 3 ∂ S 3 ∂ S 3 ∂ S 2 ∂ S 2 ∂ S 1 ∂ S 1 ∂ W 因为有： O 3 = V S 3 + b 2 S 3 = U X 3 + W S 2 + b 1 S 2 = U X 2 + W S 1 + b 1 S 1 = U X 1 + W S 0 + b 1 \begin{aligned} &\frac{\partial L_3}{\partial V}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial V} \\ &\frac{\partial L_3}{\partial U}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial U}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial U}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial S_1}\frac{\partial S_1}{\partial U} \\&\frac{\partial L_3}{\partial W}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial W}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial W}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial S_1}\frac{\partial S_1}{\partial W} \\ &因为有：\\&O_3 = VS_3 + b_2\\&S_3 =UX_3+WS_2+b_1\\&S_2 =UX_2+WS_1+b_1\\&S_1=UX_1+WS_0+b_1 \end{aligned} ​∂V∂L3​​=∂O3​∂L3​​∂V∂O3​​∂U∂L3​​=∂O3​∂L3​​∂S3​∂O3​​∂U∂S3​​+∂O3​∂L3​​∂S3​∂O3​​∂S2​∂S3​​∂U∂S2​​+∂O3​∂L3​​∂S3​∂O3​​∂S2​∂S3​​∂S1​∂S2​​∂U∂S1​​∂W∂L3​​=∂O3​∂L3​​∂S3​∂O3​​∂W∂S3​​+∂O3​∂L3​​∂S3​∂O3​​∂S2​∂S3​​∂W∂S2​​+∂O3​∂L3​​∂S3​∂O3​​∂S2​∂S3​​∂S1​∂S2​​∂W∂S1​​因为有：O3​=VS3​+b2​S3​=UX3​+WS2​+b1​S2​=UX2​+WS1​+b1​S1​=UX1​+WS0​+b1​​
可以看到U和W对于序列产生了依赖，并且可以得到：
∂ L t ∂ U = ∑ k = 0 t ∂ L t ∂ O t ∂ O t ∂ S t ( ∏ j = k + 1 t ∂ S j ∂ S j − 1 ) ∂ S k ∂ U ∂ L t ∂ W = ∑ k = 0 t ∂ L t ∂ O t ∂ O t ∂ S t ( ∏ j = k + 1 t ∂ S j ∂ S j − 1 ) ∂ S k ∂ W \begin{aligned} &\frac{\partial L_t}{\partial U}= \sum_{k=0}^{t}\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}(\prod_{j=k+1}^{t}\frac{\partial S_j}{\partial S_{j-1}})\frac{\partial S_k}{\partial U}\\&\frac{\partial L_t}{\partial W}= \sum_{k=0}^{t}\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}(\prod_{j=k+1}^{t}\frac{\partial S_j}{\partial S_{j-1}})\frac{\partial S_k}{\partial W} \end{aligned} ​∂U∂Lt​​=k=0∑t​∂Ot​∂Lt​​∂St​∂Ot​​(j=k+1∏t​∂Sj−1​∂Sj​​)∂U∂Sk​​∂W∂Lt​​=k=0∑t​∂Ot​∂Lt​​∂St​∂Ot​​(j=k+1∏t​∂Sj−1​∂Sj​​)∂W∂Sk​​​
最后将结果放入激活函数即可

四、时间序列预测

预测一个正弦函数的走势
第一部分：构建样本数据

start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

第二部分：构建循环神经网络结构

class Net(nn.Module):

    def __init__(self, ):
        super(Net, self).__init__()

        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=1,
            batch_first=True,
        )
        for p in self.rnn.parameters():
          nn.init.normal_(p, mean=0.0, std=0.001)

        self.linear = nn.Linear(hidden_size, output_size)

    def forward(self, x, hidden_prev):

       out, hidden_prev = self.rnn(x, hidden_prev)
       # [b, seq, h]
       out = out.view(-1, hidden_size)
       out = self.linear(out) # [seq,h] => [seq,1]
       out = out.unsqueeze(dim=0)# [1,seq,1]
       return out, hidden_prev

第三部分：迭代训练并计算loss

model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr)

hidden_prev = torch.zeros(1, 1, hidden_size)

for iter in range(6000):
    start = np.random.randint(10, size=1)[0]
    time_steps = np.linspace(start, start + 10, num_time_steps)
    data = np.sin(time_steps)
    data = data.reshape(num_time_steps, 1)
    x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
    y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

    output, hidden_prev = model(x, hidden_prev)
    hidden_prev = hidden_prev.detach() #不会具有梯度

    loss = criterion(output, y)
    model.zero_grad()
    loss.backward()
    optimizer.step()

    if iter % 100 == 0:
        print("Iteration: {} loss {}".format(iter, loss.item()))

第四部分：绘制预测值并比较

predictions = []
input = x[:, 0, :]
for _ in range(x.shape[1]):
  input = input.view(1, 1, 1)
  (pred, hidden_prev) = model(input, hidden_prev)
  input = pred
  predictions.append(pred.detach().numpy().ravel()[0])

x = x.data.numpy().ravel()
y = y.data.numpy()
plt.scatter(time_steps[:-1], x, s=90)
plt.plot(time_steps[:-1], x)

plt.scatter(time_steps[1:], predictions)
plt.show()

迭代200次的图像：
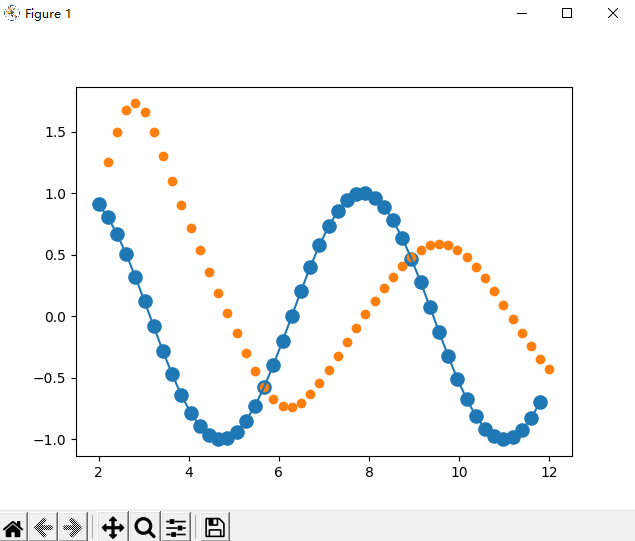
image-20230309201951030
迭代6000次的图像：
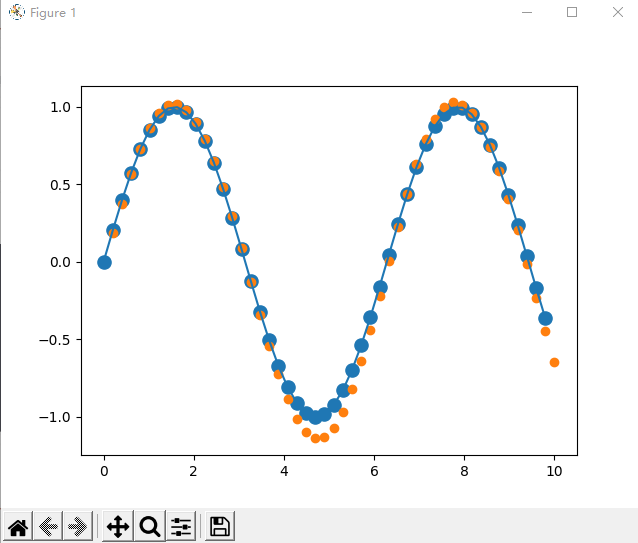
image-20230309194409606
完整代码：

import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from matplotlib import pyplot as plt
num_time_steps = 50
input_size = 1
hidden_size = 16
output_size = 1
lr=0.01

class Net(nn.Module):

    def __init__(self, ):
        super(Net, self).__init__()

        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=1,
            batch_first=True,
        )
        for p in self.rnn.parameters():
          nn.init.normal_(p, mean=0.0, std=0.001)

        self.linear = nn.Linear(hidden_size, output_size)

    def forward(self, x, hidden_prev):

       out, hidden_prev = self.rnn(x, hidden_prev)
       # [b, seq, h]
       out = out.view(-1, hidden_size)
       out = self.linear(out) # [seq,h] => [seq,1]
       out = out.unsqueeze(dim=0)# [1,seq,1]
       return out, hidden_prev

model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr)

hidden_prev = torch.zeros(1, 1, hidden_size)

for iter in range(200):
    start = np.random.randint(10, size=1)[0]
    time_steps = np.linspace(start, start + 10, num_time_steps)
    data = np.sin(time_steps)
    data = data.reshape(num_time_steps, 1)
    x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
    y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

    output, hidden_prev = model(x, hidden_prev)
    hidden_prev = hidden_prev.detach() #不会具有梯度

    loss = criterion(output, y)
    model.zero_grad()
    loss.backward()
    optimizer.step()

    if iter % 100 == 0:
        print("Iteration: {} loss {}".format(iter, loss.item()))

start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

predictions = []
input = x[:, 0, :]
for _ in range(x.shape[1]):
  input = input.view(1, 1, 1)
  (pred, hidden_prev) = model(input, hidden_prev)
  input = pred
  predictions.append(pred.detach().numpy().ravel()[0])

x = x.data.numpy().ravel()
y = y.data.numpy()
plt.scatter(time_steps[:-1], x, s=90)
plt.plot(time_steps[:-1], x)

plt.scatter(time_steps[1:], predictions)
plt.show()

五、梯度弥散和梯度爆炸问题

  • 梯度弥散(消失）：由于导数的链式法则，连续多层小于1的梯度相乘会使梯度越来越小，最终导致某层梯度为0。梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系
  • 梯度爆炸：初始化权值过大，梯度更新量是会成指数级增长的，前面层会比后面层变化的更快，就会导致权值越来越大

上面两个问题都是RNN训练时的难题，解决它们需要不断的实操经验和更加升入的理解

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/399525.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Revit导出CAD图纸操作及批量导出

Revit导出CAD图纸操作及批量导出

一、Revit如何导出CAD格式图纸 1.打开Revit模型。 2.项目浏览器，图纸(全部)，鼠标右键点击，新建图纸。 3.选择自己需要的图纸大小，点击“确定”，即可创建一张图纸。 4.找到想要导出的图纸标高或者立面，例如&…
阅读更多...
idea leetcode插件无法登录

idea leetcode插件无法登录

em 2022某天 leetcode-cn.com 改为了 leetcode.cn so , 如果是版本比较老idea leetcode插件, 就无法使用了. 因为用的旧域名 先说解决办法: 2.0 先把旧版本卸载了 2.1 ideaplugin官网找到本地idea版本下可安装的最高版本的leetcode.cn 假设是 leetcode-editor-6.9.zip 2.2 下…
阅读更多...
2023年3.8女神节买台灯怎么挑选？台灯用什么样的比较好

2023年3.8女神节买台灯怎么挑选？台灯用什么样的比较好

最近女神节，祝广大女性朋友们节日快乐啊。娱乐之余，一些实用的东西也是非常适合作为礼物送给女性朋友哦，台灯就是其中一个不错的选择。 台灯作为一种智能家居产品，不仅可见点缀卧室房间装饰，晚上的时候开启小范围照明&…
阅读更多...
uniapp+uniCloud实战项目报修小程序开发

uniapp+uniCloud实战项目报修小程序开发

前言 本项目基于 uniapp uniCloud 云开发，简单易用，逻辑主要是云数据库的增删查改，页面大部分自写，部分使用uniUI, uView 组件库。大家可用于学习或者二次开发，有什么不懂的地方可联系 wechat：MrYe443。用…
阅读更多...
2023-03-09 MySQL源码分析-MySQL中的直方图

2023-03-09 MySQL源码分析-MySQL中的直方图

摘要: 直方图的在查询优化中的作用主要是为了优化器中的代价模型提供代价中的统计信息计算, 本文对其进行分析 Histogram In MySQL mysql hitograms目录中为mysql所提供的直方图的相关基础设施代码。在mysql 8.0之前其没有使用直方图作为统计信息来为查询优化提供支持。 早期的…
阅读更多...
请教大神们，pmp考试和复习有什么攻略诀窍吗？

请教大神们，pmp考试和复习有什么攻略诀窍吗？

PMP考试通过率挺高的，很多考生也是朝九晚五甚至天天加班的打工人，还是有很多人通过了的，我也是下班后和周末才有时间学习的，3A通过，但不是什么考试大神，每天抽出3-4个小时跟着培训机构制定的学习计划学习&a…
阅读更多...
Linux高并发服务器之Linux多线程开发

Linux高并发服务器之Linux多线程开发

Linux高并发服务器之Linux多线程开发一、线程概述二、线程操作相关函数1、创建线程2、线程终止3、线程连接4、线程分离5、线程取消6、线程属性三、线程同步1、多线程卖票案例2、互斥锁解决卖票问题3、读写锁优化卖票问题4、生产者消费者模型5、条件变量解决生产者消费者问题6、…
阅读更多...
[ 云计算 | Azure ] Episode 03 | 描述云计算运营中的 CapEx 与 OpEx，如何区分 CapEx 与 OpEx

[ 云计算 | Azure ] Episode 03 | 描述云计算运营中的 CapEx 与 OpEx，如何区分 CapEx 与 OpEx

正常情况如果你不是会计，或者对钱相关的数字比较敏感的财务，本文的一些东西你不会接触的，但是最为云架构或者云运营，你可能会遇到如何采购亦或者估算的我成本和运营成本等等，所以本文的一些知识点就需要进行一定的了解…
阅读更多...
哪款蓝牙耳机音质好？内行推荐四款高音质蓝牙耳机

哪款蓝牙耳机音质好？内行推荐四款高音质蓝牙耳机

蓝牙耳机经过近几年的快速发展，在音质上的表现也越来越好。哪款蓝牙耳机音质好？最近看到很多人问。接下来，我来给大家推荐四款高音质蓝牙耳机，可以当个参考。 一、南卡小音舱蓝牙耳机 参考价：246 发声单元&#xff…
阅读更多...
900万英镑！光量子计算公司PsiQuantum获得英国政府支持

900万英镑！光量子计算公司PsiQuantum获得英国政府支持

PsiQuantum的模块化量子计算系统使用传统光纤将单个低温单元联网。（图片来源：网络）3月6日，PsiQuantum宣布，在英格兰西北部STFC的Daresbury实验室，开设先进研发设施。这项工作得到了英国政府科学创新和技术部…
阅读更多...
HTTP加密/HTTPS工作过程

HTTP加密/HTTPS工作过程

31.HTTPS即HTTP加密 前言 工作过程清楚明白！！！ 本质上是在讲SSL，适用面很广。不用再深挖了，密码学不用了解太多 SSL和TSL，本质上是一类东西 之后可以看看123 文章目录31.HTTPS即HTTP加密前言一、什么是HTT…
阅读更多...
C++基础——C++面向对象之数据封装、数据抽象与接口基础总结

C++基础——C++面向对象之数据封装、数据抽象与接口基础总结

【系列专栏】：博主结合工作实践输出的，解决实际问题的专栏，朋友们看过来！ 《项目案例分享》 《极客DIY开源分享》 《嵌入式通用开发实战》 《C语言开发基础总结》 《从0到1学习嵌入式Linux开发》 《QT开发实战》 《Android开发实…
阅读更多...
打怪升级之字符串的分界符与字符串替换

打怪升级之字符串的分界符与字符串替换

流的字符串分界符 在C的iostream中，有流的字符串分界符： " “和”"都代表简单的分隔。 因此，使用流来做字符串分隔的话，有一个比较简单的方案就是将原定义的分隔符通过替换的方式变成流的分隔符。然后再录入流中就能…
阅读更多...
【论文简述】Learning Optical Flow with Kernel Patch Attention（CVPR 2022）

【论文简述】Learning Optical Flow with Kernel Patch Attention（CVPR 2022）

一、论文简述 1. 第一作者：Ao Luo 2. 发表年份：2022 3. 发表期刊：CVPR 4. 关键词：光流、局部注意力、空间关联、上下文关联 5. 探索动机：现有方法主要将光流估计视为特征匹配任务，即学习在特征空间中将…
阅读更多...
软件设计师教程（十）计算机系统知识-结构化开发

软件设计师教程（十）计算机系统知识-结构化开发

软件设计师教程 软件设计师教程（一）计算机系统知识-计算机系统基础知识 软件设计师教程（二）计算机系统知识-计算机体系结构 软件设计师教程（三）计算机系统知识-计算机体系结构 软件设计师教程（…
阅读更多...
Zookeeper3.5.7版本——客户端命令行操作（节点删除与查看）

Zookeeper3.5.7版本——客户端命令行操作（节点删除与查看）

目录一、节点删除示例1.1、节点删除1.2、递归节点删除二、查看节点状态示例一、节点删除示例 1.1、节点删除 在客户端上创建 test 节点，并查看该节点 [zk: localhost:2181(CONNECTED) 5] create /test "123456"删除 test 节点，并查看该节点 […
阅读更多...
初识rollup 打包、配置vue脚手架

初识rollup 打包、配置vue脚手架

rollup javascript 代码打包器，它使用了 es6 新标准代码模块格式。 特点： 面向未来，拥抱 es 新标准，支持标准化模块导入、导出等新语法。tree shaking 静态分析导入的代码。排除未实际引用的内容兼容现有的 commonJS 模块&#…
阅读更多...
Sqoop详解

Sqoop详解

目录 一、sqoop基本原理 1.1、何为Sqoop？ 1.2、为什么需要用Sqoop？ 1.3、关系图 1.4、架构图 二、Sqoop可用命令 2.1、公用参数：数据库连接 2.2、公用参数：import 2.3、公用参数：export 2.4、公用参数&#xff…
阅读更多...
MySQL数据库和表管理

MySQL数据库和表管理

MySQL数据库和表管理一、常用的数据类型1、int(N)2、float(m,d)3、char与varchar二、查看数据库结构1、查看当前服务中的数据库2、查看数据库中存在的表3、查看表结构三、SQL语句1、SQL语言规范2、SQL语言分类四、创建、删除数据库和表1、创建数据库2、创建表3、删除数据表4、删…
阅读更多...
云医疗信息系统源码（云HIS）商业级全套源代码

云医疗信息系统源码（云HIS）商业级全套源代码

云his系统源码，有演示 一个好的HIS系统，要具有开放性，便于扩展升级，增加新的功能模块，支撑好医院的业务的拓展，而且可以反过来给医院赋能，最终向更多的患者提供更好地服务。 私信了解更多&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023