目录
八、算法
8.1 概念
8.1.1 非正式定义
8.1.2 示例
8.1.3 定义动作
8.1.4 细化
8.1.5 泛化
8.2 三种结构
8.2.1 顺序
8.2.2 判断
8.2.3 循环
8.3 算法的表示
8.3.1 UML
8.3.2 伪代码
8.4 更正式的定义
8.5 基本算法
8.5.1 求和
8.5.2 求积
8.5.3 最大和最小值
8.5.4 排序
8.5.5 查找
8.6 子算法
8.6.1 结构图
8.7 递归
8.7.1 迭代的定义
8.7.2 递归的定义
八、算法
8.1 概念
8.1.1 非正式定义
算法的一种非正式概念如下:算法是一种逐步解决问题或完成任务的方法。
按照这种定义,算法完全独立于计算机系统。算法需要一组输入数据,并产生一组输出数据。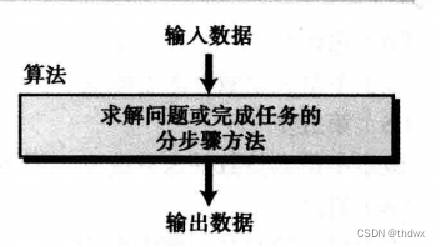
8.1.2 示例
现在我们要得到一组输入数据(都是整数)里的最大值,为了方便分析算法,我们假设要找到五个输入数据里的最大值,显然这个任务不可能一步完成,根据小学的数学知识,这个算法可以用以下几步实现:
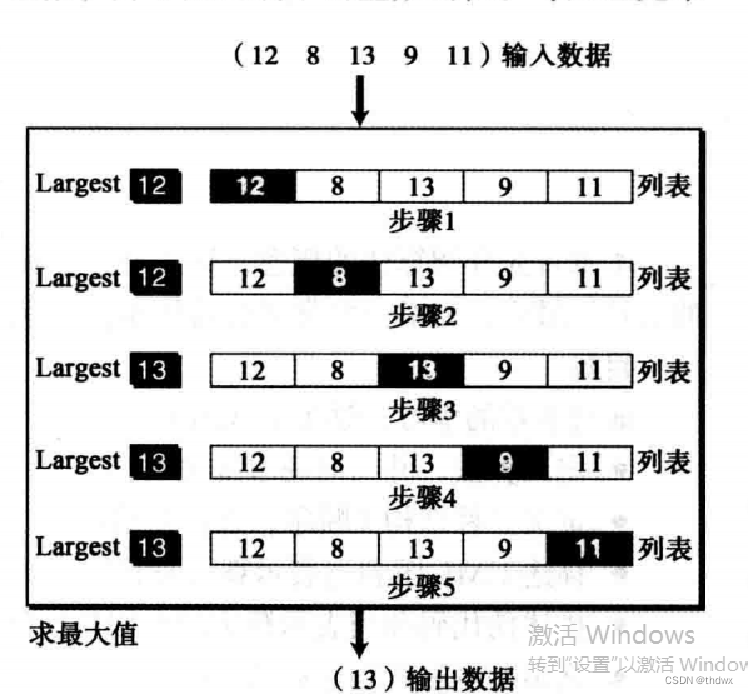
首先检查第一个整数,由于还没有检查其他整数,所以将最大值设为12;
检查第二个数,发现8小于12,所以最大值仍为12;
检查第三个数,发现13大于12,所以最大值变为13;
检查第四个数,发现9小于13,最大值不变;
检查第五个数,发现11小于13,最大值不变。
经过五个步骤就可以得出这组数中的最大值为13.
8.1.3 定义动作
将上述五个步骤定义为五个动作,通过算法中的这五个动作就可以找到数据中的最大值。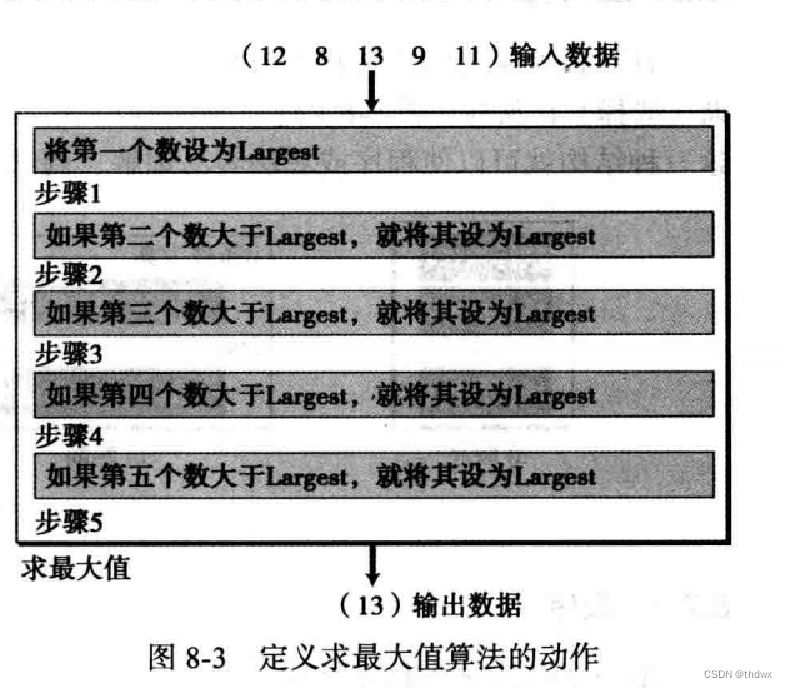
8.1.4 细化
为了使算法能在所有的程序中使用,还需要进行细化。现在有两个问题:第一步中的动作和其他步不一样;第二步到第五步中的程序描述语言不同。对动作进行改进后可以得到: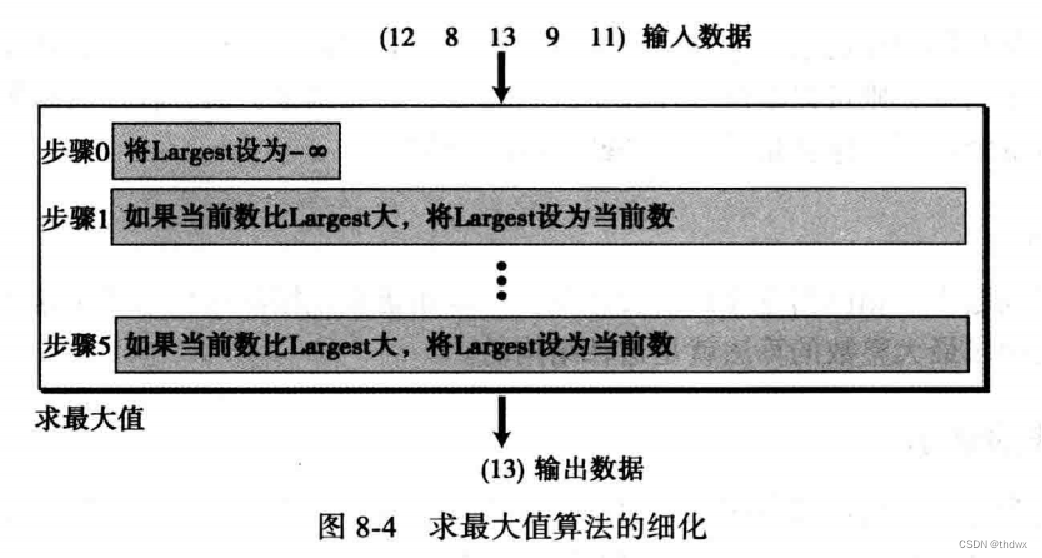
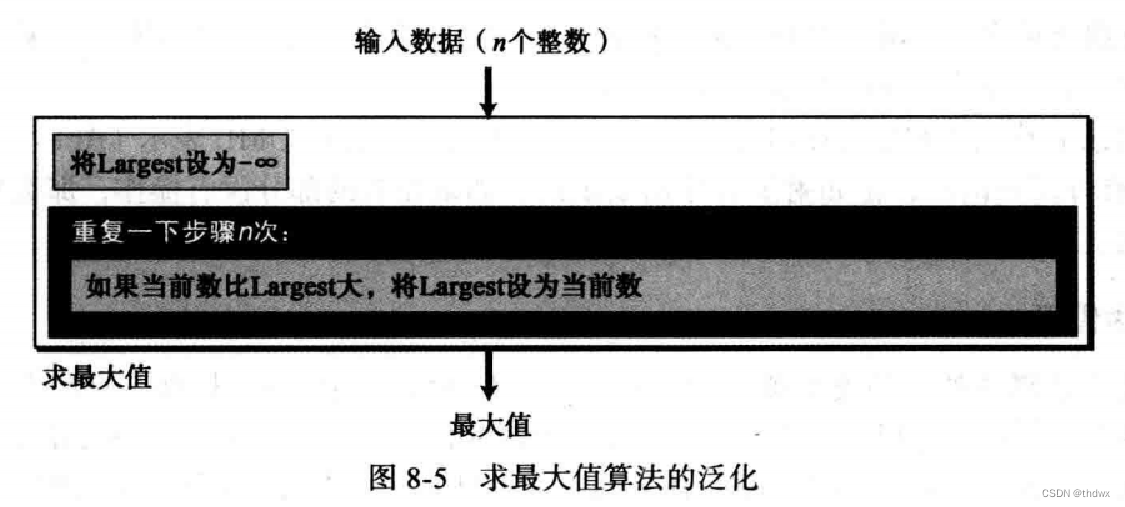
8.1.5 泛化
将这个算法推广到 个数中找最大值,只要让计算机循环步骤一
次。
8.2 三种结构
计算机专家为结构化程序或算法定义了三种结构。这种想法认为程序必定是由顺序、判断(选择)、循环三种结构组成的,已经证实其他结构都是不必要的。仅仅使用这三种结构就可以使程序或算法容易理解、调试或修改。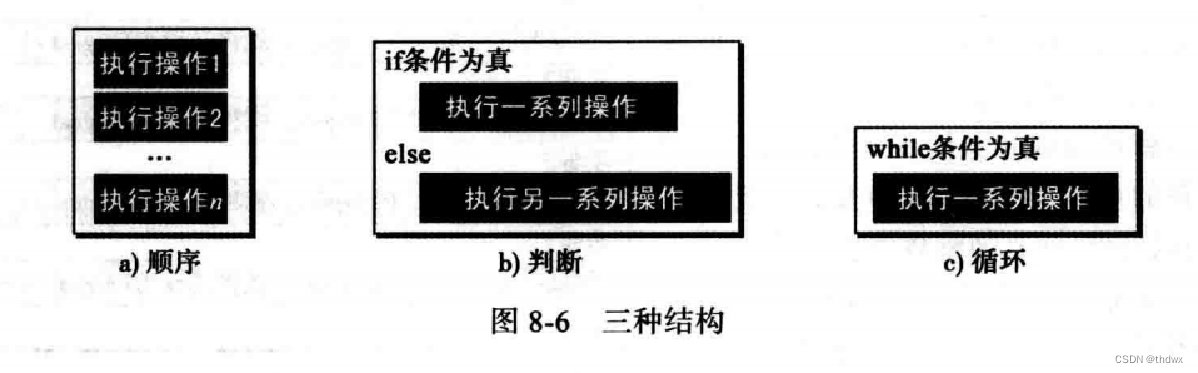
8.2.1 顺序
第一个结构称为顺序结构。算法(最终是程序)都是指令序列,可以是简单指令或是其他两种结构之一。
8.2.2 判断
有些问题只用简单指令是无法解决的。有时候需要检测一个条件,当这个条件满足时执行一系列操作;这个条件不满足时执行另外一系列操作。这就是判断(选择)结构。
8.2.3 循环
在有些问题中,相同的指令需要重复,可以使用循环结构来解决这个问题。
8.3 算法的表示
8.3.1 UML
统一建模语言(UML)是算法的图形表示。它使用“大图”的形式掩盖了算法的所有细节,只显示算法从开始到结束的整个流程。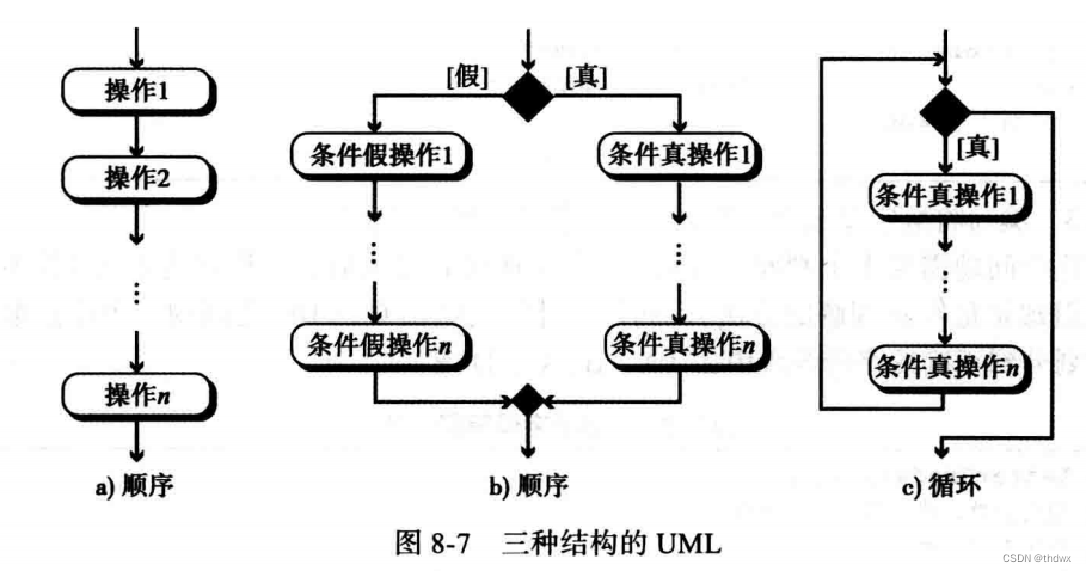
8.3.2 伪代码
伪代码是算法的一种类似英语的表示法,现在还没有伪代码的标准。伪代码与真正的代码相似,区别就是伪代码无法运行。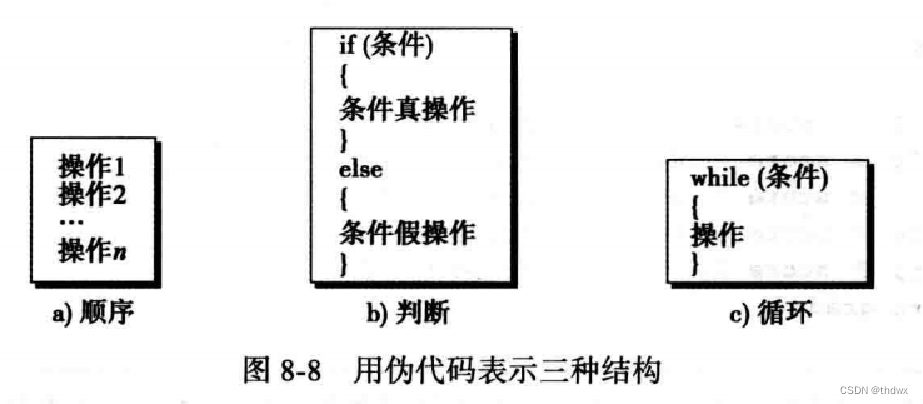

8.4 更正式的定义
算法是一组明确步骤的有序集合,它产生结果并在有限时间内终止。
定义良好:算法必须是一组定义良好的且有序的指令集合。在数学中,定义良好的函数指的是相同的自变量应该有相同的函数值、对于每一个存在的自变量都应该存在对应的函数值。放在算法中可以理解为,算法对于所有可能的输入都是有效。
明确步骤:算法的每一步都必须有清晰、明白的定义,不能产生歧义。
产生结果:算法必须产生结果,否则算法就是无意义的。这个结果可以是数据也可以是产生的其他影响。
有限时间内终止:算法必须能够在有限时间内终止,否则就不能叫算法(例如无限循环)。
8.5 基本算法
这里讨论算法只是概括性的描述思路,算法的理解和实现要在学习了编程语言后才能明白的更透彻。
8.5.1 求和
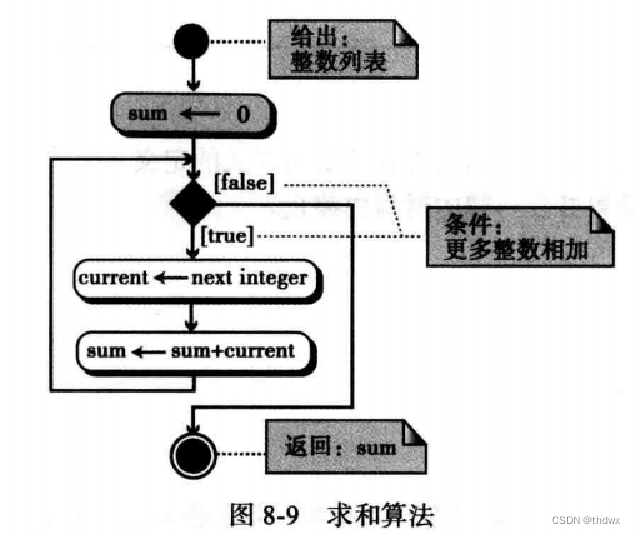
分为三个逻辑部分:
将和(sum)初始化;
循环,在每次迭代中将新的数加到和上;
退出循环并返回结果。
8.5.2 求积
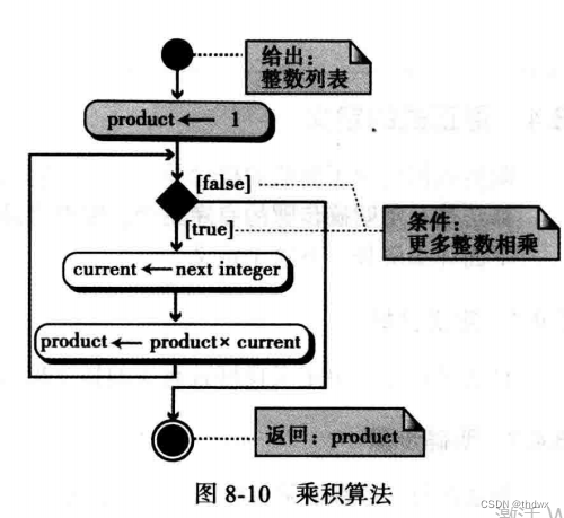
分为三个逻辑部分:
将积(product)初始化;
循环,每次迭代将新的数乘到积上;
退出循环后返回结果。
8.5.3 最大和最小值
在本文最开始已经描述过,最大和最小不同的地方在于,一个在初始化时要使用很小的数,一个在初始化时要使用很大的数。
8.5.4 排序
计算机科学中一个最普遍应用是排序,即根据数据的值对它们进行排列。如果没有排序,查找会变得非常困难。例如,在一个杂乱无序的通讯录里找一个人是非常困难的,但如果按照某种规则排好序,那么就会方便很多。
下面简单介绍三种最基础排序算法的思路。
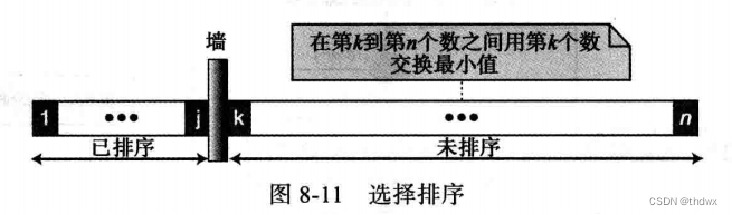
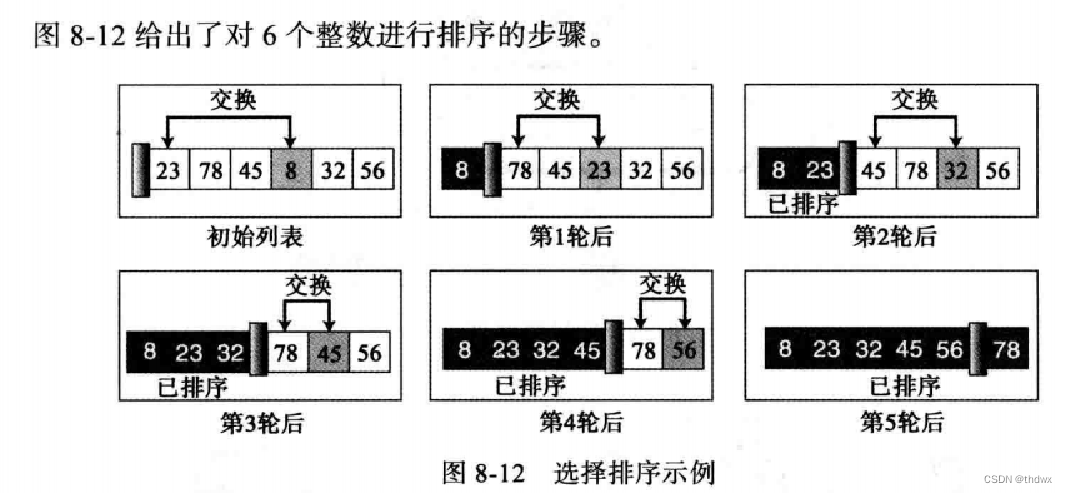
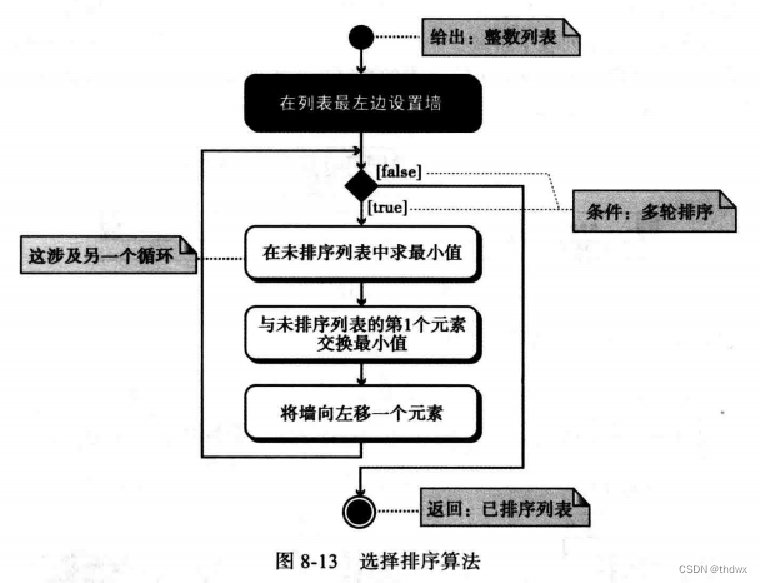
1. 选择排序
在选择排序中,将待排序的数列分为两个部分,已排序子列表和未排序子列表。每次循环找到未排序子列表中的最小值(也可以是最大值)并与未排序子列表中的第一个元素交换位置,算法开始的时候,整个列表都是未排序子列表。 个数的列表需要
轮完成排序,最后一个数是排好序的,不需要再循环。
2. 冒泡排序
在冒泡排序中,也将列表分为已排序子列表和未排序子列表。在每次循环中,从未排序子列表的第一个元素开始,元素之间两两比较(第一个和第二个比,第二个和第三个比,依次下去),当前一个元素较大(较小)时,两元素交换位置,这样每轮比较之后,未排序子列表中最小(最大)的元素就像气泡一样慢慢冒到未排序子列表最前端,在算法开始时,整个列表都是未排序子列表。 个数的列表需要
轮完成排序,最后一个数是排好序的,不需要再循环。
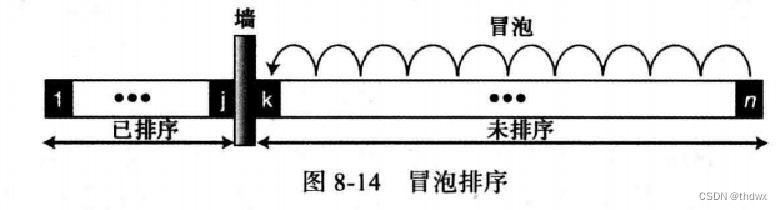
图中冒泡排序算法,元素从后往前比较,但不管从前往后还是从后往前,其本质和效率都是相同的。
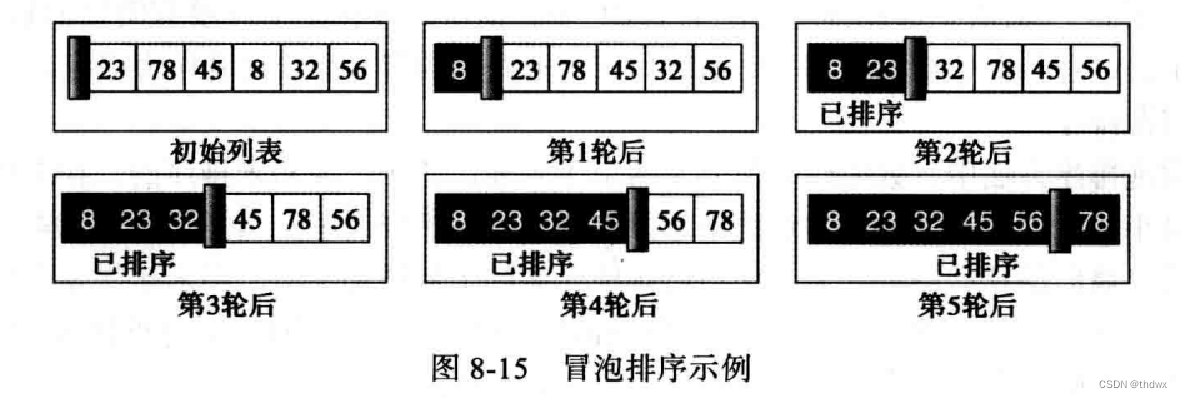
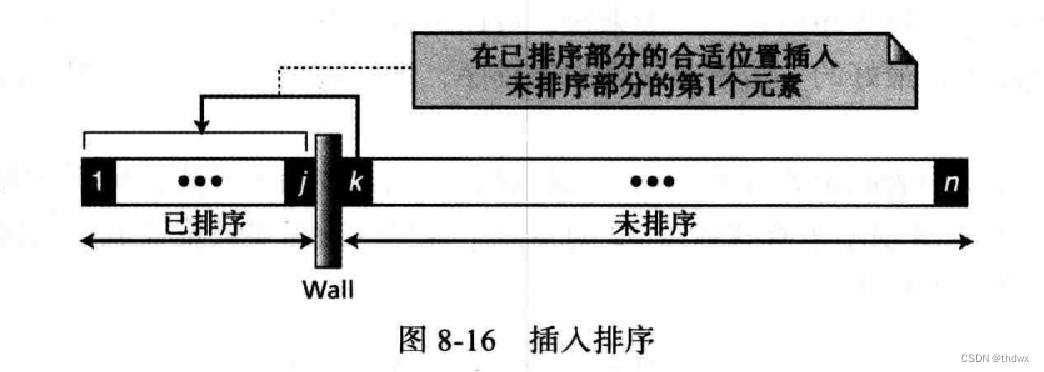
3. 插入排序
在插入排序中,列表也被分为已排序子列表和未排序子列表。在每次循环中,拿出列表当前位置的元素,并将它插入到已排序列表中的合适位置,就像接扑克牌一样,新的数(牌)只要插入到排好序序列的合适位置,整个序列就是有序的,与前两个算法不同的是,在算法开始时,第一个位置认为是已排序的,因为只有一个数,所以它就在它应该插入的位置,插入从第二个位置的元素开始,直到最后一个元素正确插入。 个数的列表需要
轮完成排序。

4. 其他排序算法
这三种算法是最低效的,但是它们简单易懂,还有例如快速排序、归并排序等更高效的排序算法。评价算法性能的两个指标是时间复杂度和空间复杂度,这两个概念会在后面的学习中学到。
8.5.5 查找
在计算机科学里还有一种常用的算法叫作查找,是一种在列表中确定目标所在位置的算法。
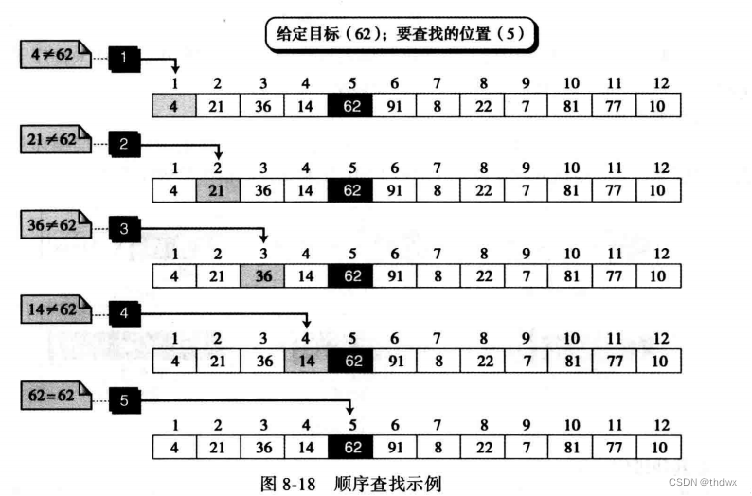
1. 顺序查找
用于在无序且较小的列表中查找,通过检查列表中的每个元素,找到目标元素所在的位置。如果列表有序或是很大,那么有更高效的查找算法。
2. 折半查找(二分法)
用于有序数列中的查找。首先找到数列的中间元素(通过数列最左侧坐标与最右侧坐标之和除以2来找到),如果要查找的数比它大,那么就应该在它的右边(或左边)查找,如果比它小,就应该在左边(或右边)查找,如果刚好等于它,那么直接返回。当确定要查找的半区后,将这个半区看成新的数列,但是坐标仍然使用它在原数列的坐标,对这个半区重新使用相似的方法,由于中间元素已经考察过,所以在更新最左侧或最右侧坐标时要去掉中间元素。如此循环,直到更新后的最左侧坐标大于最右侧坐标(说明查找的值不存在)或是找到目标值。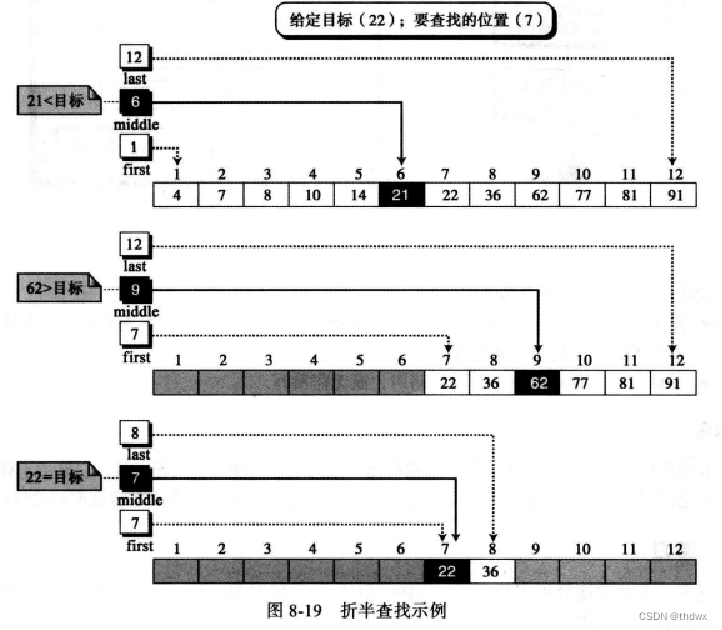
8.6 子算法
结构化编程要求将算法分成几个单元,称为子算法。每个子算法又分为更小的子算法。使用子算法的优点是:程序更容易理解;子算法可在主算法中的不同地方调用,无须重写。
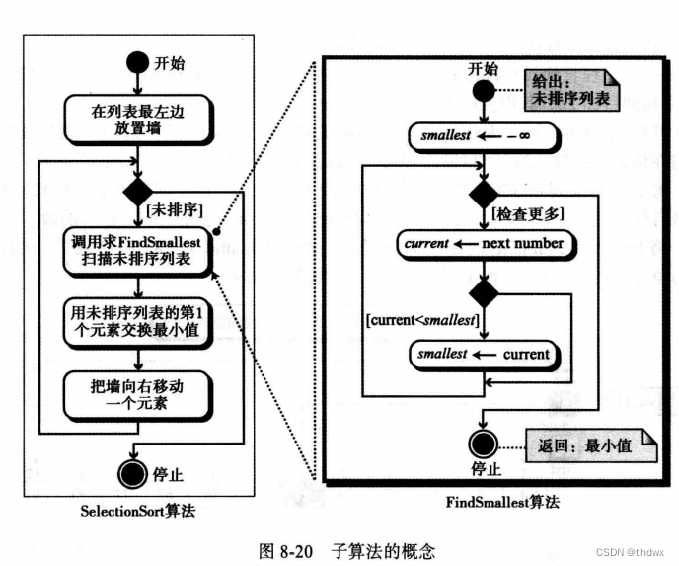
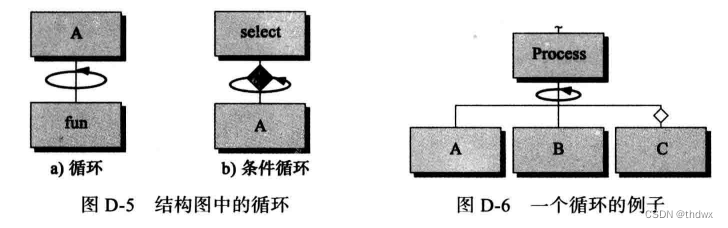
8.6.1 结构图
程序员使用的另一个工具是结构图。结构图是一种高级设计工具,它显示算法和子算法之间的关系,它一般在设计阶段使用。结构图一般从上到下、从左到右阅读。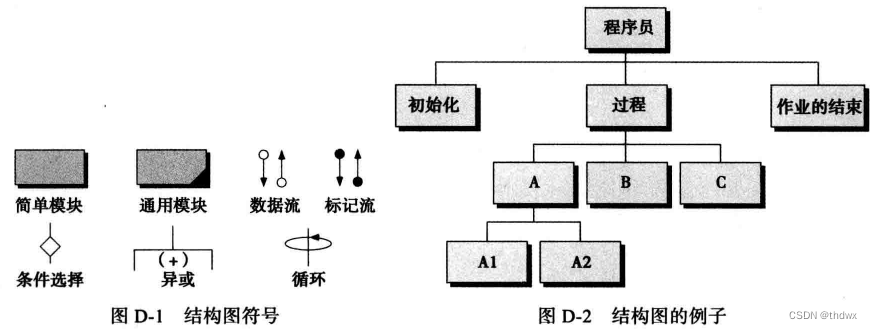
8.7 递归
8.7.1 迭代的定义
如果算法的定义不涉及算法本身,则算法是迭代的。例如,求阶乘的迭代定义:
8.7.2 递归的定义
当一个算法出现在它本身的定义中,这个算法就是递归的。例如,求阶乘的递归定义:
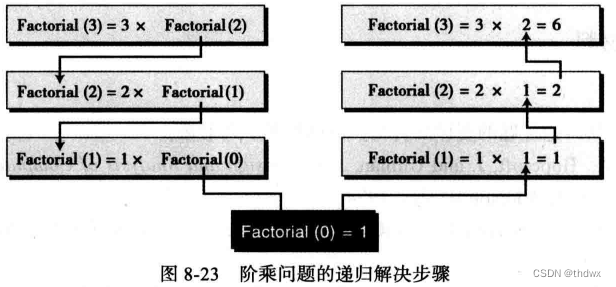
递归实际上是将一个复杂问题由高到低分解,并从低到高解决这个问题。 








![Mysql问题:[Err] 1055 - Expression #1 of ORDER BY clause is not in GROUP BY clause](https://img-blog.csdnimg.cn/1066a58e1b5d4b119df843e604651406.png)