一、题目描述

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

二、示例输入输出

示例1：

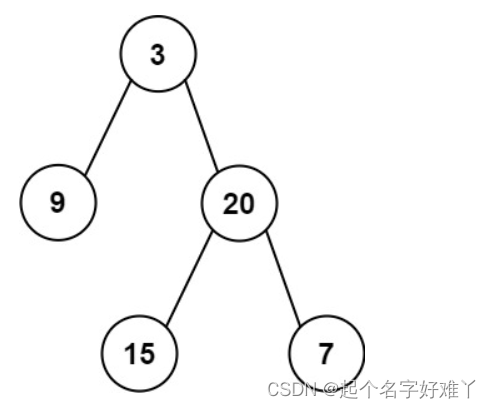
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

三、题目解析 & 解题思路

思路可知输入为前序遍历、中序遍历
前序遍历：前序遍历顺序为 根左右 即 先访问根，再遍历左子树，再遍历右子树
中序遍历：中序遍历顺序为 左根右 即 先访问左子树，再访问根节点，最后访问 右子树
前序遍历顺序特点：第一个 为根节点 例如 示例 1 为: 3 9 20 15 7 可以得知 节点 3 为整棵二叉树的根节点，再结合中序遍历 的顺序 ：9 3 15 20 7 可以得知 节点 3 左侧的 为整棵树的 左子树，节点 3 右边的为整棵树的 右子树
首先可以确定的就是根节点 为 前序遍历的第一个
如下图示例：

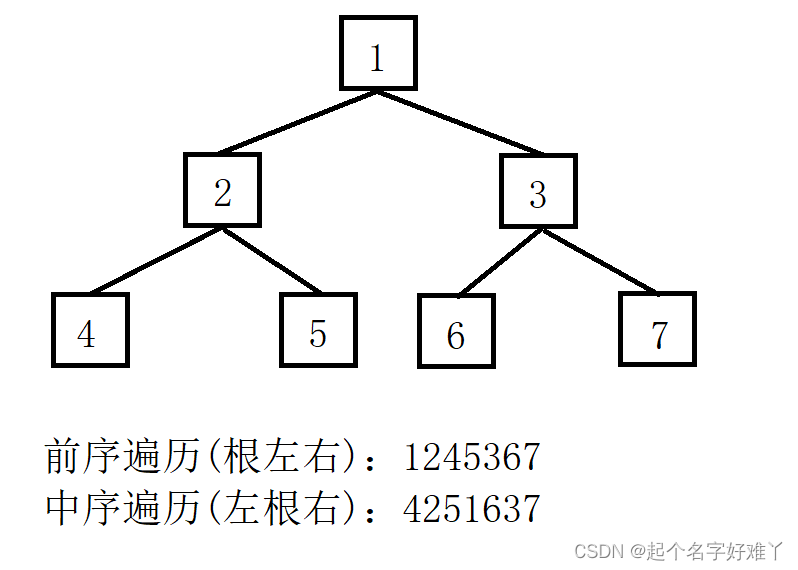
根据前序遍历特点：根左右 那么 前序遍历的结果中 左子树为 245 恰好 可以根据 中序遍历 中的根节点 1 划分 左子树 为 245 和 367 接下来 开始 根据前序 的 245 和 中序 的 425 来 判断 节点 2、4、5 这三个节点 那个是左孩子那个是右孩子即可

3.1

首先将 前序遍历中的第一个节点 作为根节点 插入到 二叉树中，若前序遍历为空 那么整个树也为空

3.2

另外 我们需要一个 栈进行辅助，保存前序遍历的节点(根节点或左孩子节点 因为 前序 根左右的 遍历顺序 会一直，根 -> 左(父) -> 左(父) 直到遍历到最后一个 左孩子 叶子节点，才会 回溯 回去 遍历 上一层的 右孩子节点)，且 右孩子节点肯定是 栈中 某一个节点的 右孩子节点
并从下标 index = 0 判断中序遍历 下标为 index 的元素 是否等于当前栈顶元素 如果等于栈顶元素，说明该子树 左孩子或父节点 已经遍历完毕

例如 假如 前序遍历和中序遍历的第一个节点都是 1 那么说明，这棵树没有左子树：

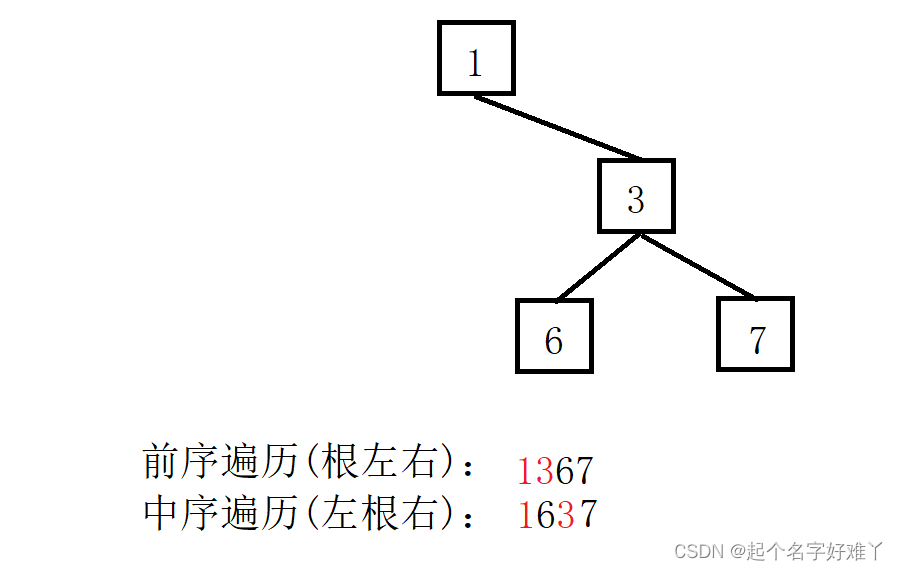
按照这样的思路 我们先 入栈 节点 124
stack [1, 2 ,4]
并且将这些节点 作为 左孩子 逐步插入，当遍历 到 前序 1245367 中的 5 时 我们发现 现在的栈顶 元素为 4 且 中序遍历顺序的第一个 元素也为 4 ，且中序遍历为 左根右 ，因此 节点 4 没有左孩子，那么在前序遍历 1245367 节点 4 的 下一个元素 5 ,肯定是 124 某一个节点 的 右孩子节点
index 依次向后移动，并和栈顶元素比较，因为栈里都是 根 左 根 左 ，栈顶到 栈底的顺序 为 左 根 左 根 ，而中序为 左 根 右 ，当 中序 下标为 index 且 与 栈顶元素相等 时，index 继续向后移动，栈 弹出 栈顶元素，当栈顶元素不等于 index 元素 时 说明遇到了 右孩子，且该节点是 上一次弹出的 节点的右孩子
即 5 != 1 则 5 为上一个弹出 的 节点 2 的 右孩子，这时 我们将 5 作为 右孩子 插入

总体思路：在前序中 构建节点的左孩子，中序中 确定 右孩子节点

四、代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size() == 0 || inorder.size() == 0)
        {
            return nullptr;
        }
        stack<TreeNode*> stkTree;
        //前序遍历结果的第一个作为 根节点插入
        TreeNode* Root = new TreeNode(preorder[0]);
        stkTree.push(Root);
        int inorderIndex = 0;
        for(int i = 1; i < preorder.size(); i++)
        {
            int iTemp = preorder[i];
            TreeNode* nodeTemp = stkTree.top();
            //从前序中构建出来左孩子节点 
            if(nodeTemp->val != inorder[inorderIndex])
            {
                TreeNode* node = new TreeNode(iTemp);
                nodeTemp->left = node;

                stkTree.push(nodeTemp->left);
            }
            else
            {
            	//从后序节点中找到 右孩子节点
                while(!stkTree.empty() && (stkTree.top()->val == inorder[inorderIndex]))
                {
                	//保存节点，最后一个弹出的为右孩子的父节点
                    nodeTemp = stkTree.top();
                    stkTree.pop();
                    ++inorderIndex;
                }
                nodeTemp->right = new TreeNode(iTemp);
                stkTree.push(nodeTemp->right);
            }
        }
        return Root;

    }
};