加法器

1. 一位全加器

$$\begin{gathered} 一位全加器，当前位输出：S_i=A_i⨁B_i⨁C_i \\ 也就是输入中有奇数个1时输出为1（异或） \\ 向高位的进位：C_i=A_i{B}_i+(A_i⨁B_i)C_{i-1} \\ 若本位均为1，或本位中一个为1并且来自低位的进位为1，那么向高位的进位就为1 \\ 进位逻辑表达式也可以写成：C_i=A_i{B}_i+(A_i+B_i)C_{i-1} \end{gathered}$$

其实一位全加器，逻辑表达式可以用与门或门表示，如进位的逻辑表达式不唯一，可以是A、B、C两两与，再或运算（也就是有两个1就进位），但这里用会用异或门和与门来表示，本质上这些逻辑表达式都是一样的。区别就是推到加法器先行进位时P的表示不一样

2. 串行加法器

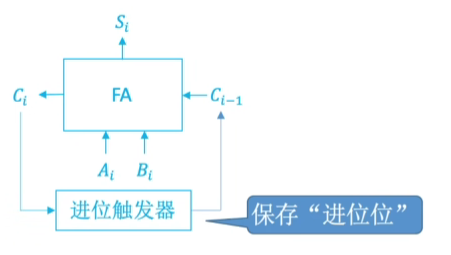
只有一个全加器，数据逐位串行送入加法器中进行运算。进位触发器用来寄存进位信号，以便参与下一次运算。

如果操作数长n位，加法就要分n次进行，每次产生一位和，并且串行逐位地送回寄存器。

3. 串行进位加法器加法器

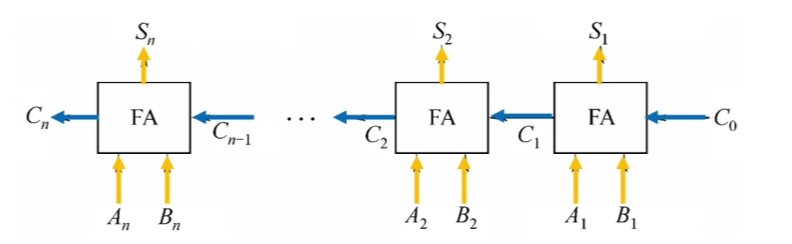
把n个全加器串接起来，就可进行两个n位数的相加。

串行进位又称为行波进位，每一级进位直接依赖于前一级的进位，即进位信号是逐级形成的。每一个加法器的计算都取决于来自低位的进位，所以串行进位加法器运算速度取决于每一个加法器求向高位进位的速度

4. 先行进位加法器

先行进位加法器：各级进位信号同时形成，又称为先行进位、同时进位

先来回顾串行进位加法器：

串行进位加法器受到进位信号延迟的影响，计算速度迟缓。所以我们可以先将向高位的进位全部一次性算出来，这样每一位加法器就不需要等待来自低位的进位了：

我们再次简化：

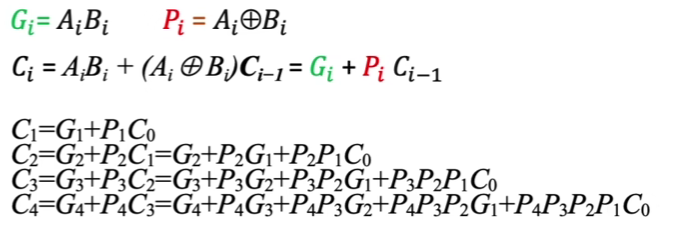
可以发现一个规律：在计算进位时，P_i和G_i不会向低位传，但一定会向高位传。也就是说高位的进位计算依赖于所有低位的P_i和G_i。相应的产生进位的该逻辑部件，我们称为CLU先行进位部件。

这总先行进位加法器随着位数不断增多，套娃越来越严重，逻辑表达式越来越复杂，也就是电路越来越复杂。所以我们一般做到4位先行进位加法器，针对更多位的加法，我们可以对4位先行进位加法器CLA进行组间串行，如下：

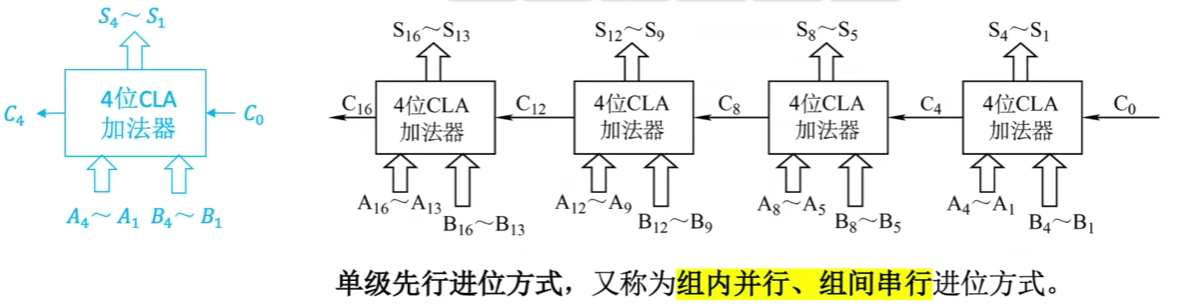
但组间串行类似串行进位加法器一样，是有延迟的。每一个4位CLA都在等待来自低位的CLA进位，卫门我们是否可以参考先行进位加法器，将组间进位再次先算出来呢？

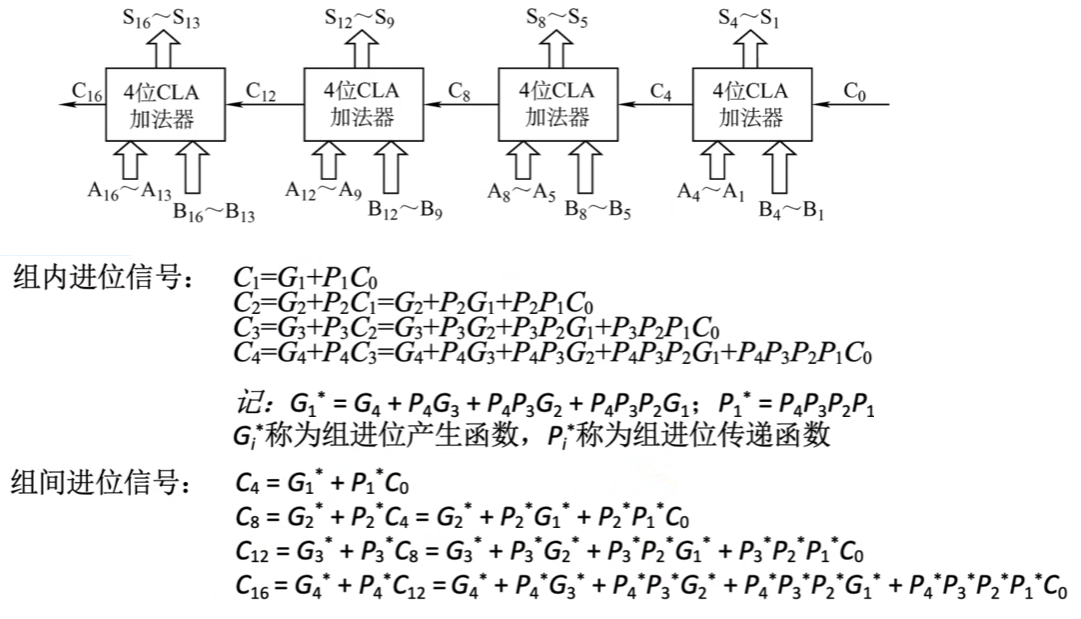
可以发现组内进位信号计算和组件进位信号的计算逻辑很相似，组内进位输入每一个位p和g即可输出进位，组间进位输入每一个4位CLA的P和G，就能产生组间进位信号了。所以说，组内进位和组件进位使用的是同一套CLU（先行进位部件，专门用于产生进位的部件CLU+全加器就可以组成CLA）。

优化过的先行进位加法器如下：（CLA电路就相当于CLU，用于产生进位的部件）

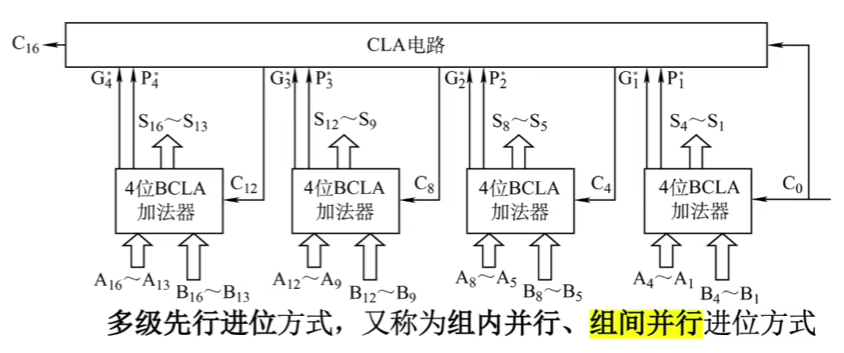
串行加法器→串行进位的并行加法器→组内并行、组间串行进位的加法器（单级先行进位方式）→组内并行、组间并行进位的加法器（多级先行进位加法器优化）