作者:KON 来源:投稿
编辑:学姐
作者介绍:Kon
擅长是自然语言处理、推荐系统,爱好是cv;著有cv相关专利一篇,西安交通大学软件专业本硕。
1.前言
本次给大家带来的是发表在「ICLR2019」上的一篇文章:「LEARNING DEEP REPRESENTATIONS BY MUTUAL INFORMATION ESTIMATION AND MAXIMIZATION。」
「这篇文章是对比学习的开山之作之一」,为对比学习提供了理论支撑,指导了后来人如何正确选择合适的对比函数损失。截至完稿,该论文的引用为1299。
本文只讨论该paper的核心部分,也就是理论推导部分,「它解释了我们如何通过最大化互信息来达成我们对比学习的目的」。虽然这篇文章主要讨论的是CV上的对比学习,但该理论是通用于所有深度学习框架的范式,把它扩展到图表示、NLP等其它领域也是合适的。
虽然这篇文章非常的经典+硬核,但遗憾的是,原论文并没有给出各公式的详细推导。如果数学功底不够扎实,读起来往往颇为费劲。本文将给出该paper有关理论详细推导+详细解释,一步步带大家理解。
2.什么是对比学习?
对比学习是一种自监督学习方法,用于在没有标签的情况下,通过让模型学习哪些数据点相似或不同来学习数据集的一般特征。
让我们从一个简单的例子开始:
假设你有两个苹果和一个梨,即使没有人告诉你它们是什么,你仍可能会意识到,与苹果相比,这两只梨子看起来很相似。仅仅通过识别它们之间的异同,我们的大脑就可以了解我们的世界中物体的高阶特征。

目前主流的深度学习是「通过对输入拟合label来达到学习目的的」,但实际情况中,可能根本没有那么多label可言。在上述例子中,并没有谁来告诉我们label,我们仍然能够学到大量的信息。基于此启发,对比学习的概念应运而生。
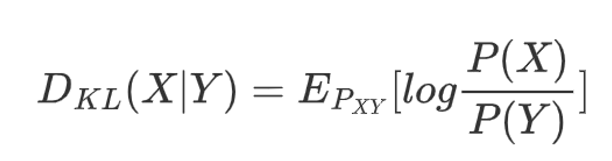
3.数学准备
在开始我们的推导之前,我们需要先明确几个后续推到会使用到的概念:
KL散度:
KL散度是用来衡量两个分布差异的度量,它是顺序敏感的,D(X|Y)与D(Y|X)是不同的。
互信息:
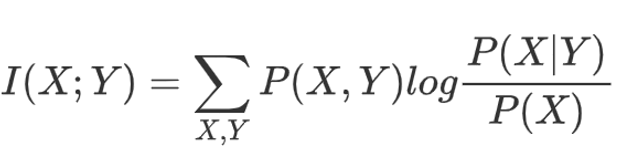
互信息描述了两个分布共有信息的度量,它是顺序不敏感的,I(X;Y)与I(Y;X)是一样的。很容易可以看到,这两个度量都可用来衡量两分布之相似性。那么,它们之间有没有关系呢?
「答案是有的,推导如下」:
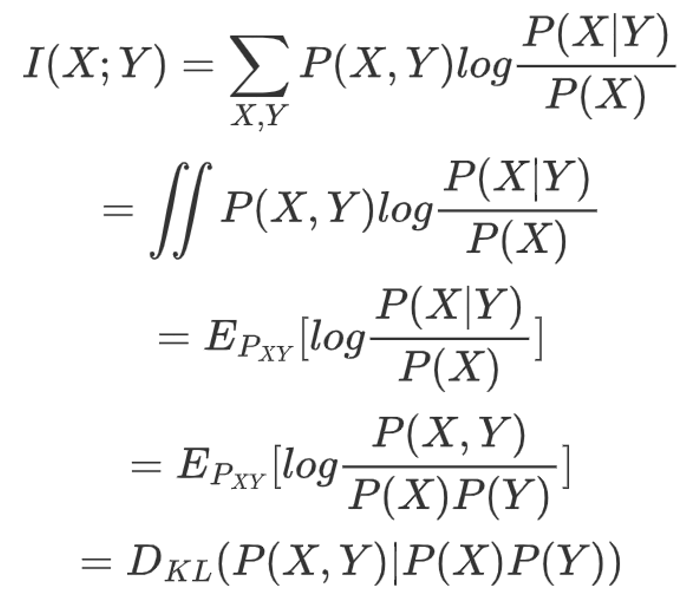
原来X与Y的互信息,就等于X与Y之联合分布与X Y边缘分布之乘积。
共轭函数:
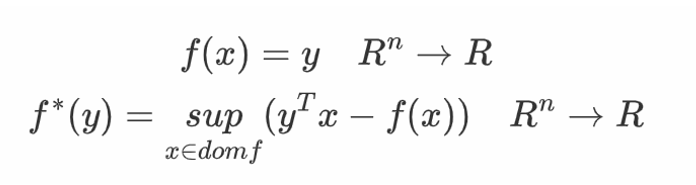
这里的sup代表上确界,即最小上界。使上述上确界有限,即差值在f之定义域有上界的所有y构成了共轭函数的定义域。共轭函数是我们后续推导的剪刀,帮助我们把目标函数剪成我们想要的样子。
4.如何最大化互信息?
对比学习是一种无监督学习,其目的是衡量两个输入的相似性。大家应该可以发现,这不恰巧与互信息的定义一致吗?那么,我们「可以使用互信息来当作我们的Loss函数吗?」
答案当然是「可以」。但难度也是显而易见的,我们有的只是样本,不知道分布具体的表达式。不知道具体的表达式就无法算得互信息的具体数值,便无法进行反向传播更新参数。
其实我们不一定非要求得互信息的解析解。长久以来的经验告诉我们,在实际应用中,数值解往往就够了。在F-GAN严格推导和证明了所有散度的下确界都由某个生成函数f与某个共轭函数g决定,于是我们借用F-GAN中的思想,希望用逼近的方法让互信息成为我们的损失函数。
由于所有散度都可归纳于一般的F-散度,为了更泛化的结果,我们不止对KL散度进行推导,将上述共轭函数带入,我们对F-散度进行推导:
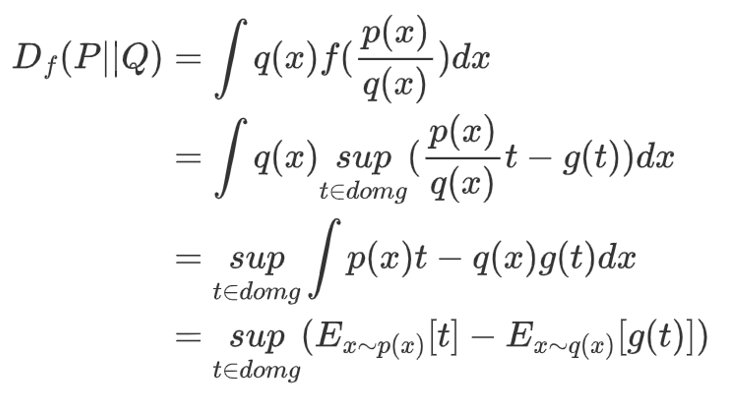
「这里t为f的输出,g为f的共轭函数。通过共轭函数这把剪刀,我们把f散度求解问题变成了求解两分布下T(x)与g(T(x))期望之最大值问题,把一个抽象的问题具体化了。」
于是,当F散度为KL散度时,使用上述推导结果,很容易就可以得到:
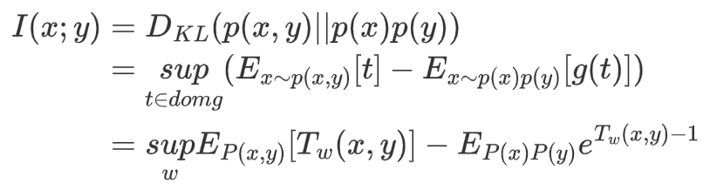
在本文中,作者借用MINE(Mutual Information Neural Estimation)的结论。MINE中使用的是Donsker-Varadhan Estimator(DV representation of KL divergence),该estimator是互信息的一个下界。DV estimator对F-GAN导出的散度解析解作了一丢丢小改动,代入KL散度便得到:
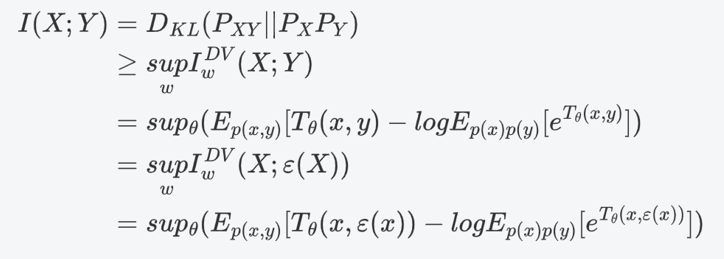
这里的epsilon为我们的encoder编码器,也就是神经网络;T为classifier分类器,也就是最后的FC层或回归头。终于,原来那么抽象的问题,现在只要令两批样本(如,一张在沙漠的波斯猫图片和一张在草地上大橘图片)的期望尽可能大,那么就能尽可能提高互信息的下限,就可以通过曲线救国的方法,最大化两批样本MI。
这个过程中,神经网络学到的就是两批样本的通用信息,如猫咪眼睛的样子、猫咪的爪子、猫咪的四肢等,噪音信息(如不同背景,沙漠、草地 etc.)等被忽略。
至此,原来无法解决的问题便解决了,对比学习打下了坚实的理论基础。再回头看一眼本文实际代码中的Global Infomax的Loss函数,其中正样本来自联合分布,负样本来自边缘分布之积,是不是就非常清晰了呢?
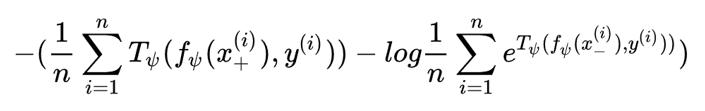
关注下方《学姐带你玩AI》🚀🚀🚀
回复“对比学习”
免费获取论文原文PDF+代码数据集
码字不易,欢迎大家点赞评论收藏!