一、概念
1.1、排序
排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
平时的上下文中,如果提到排序,通常指的是排升序(非降序)。 通常意义上的排序,都是指的原地排序(in place sort)
原地排序:就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
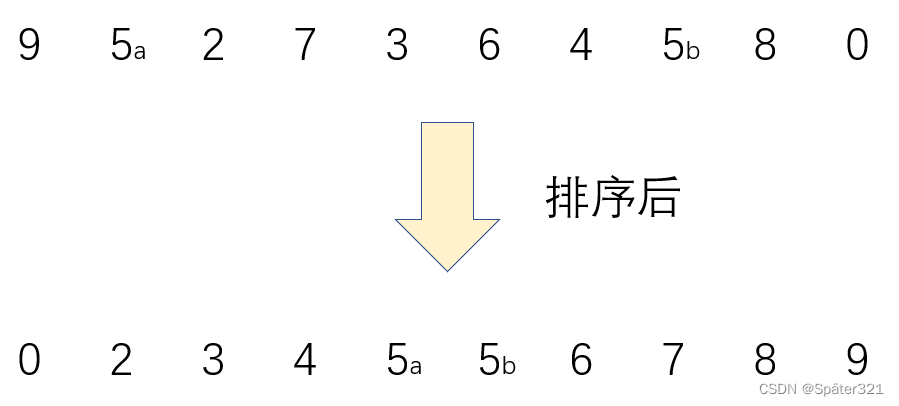
1.2、稳定性(重要)
两个相等的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法
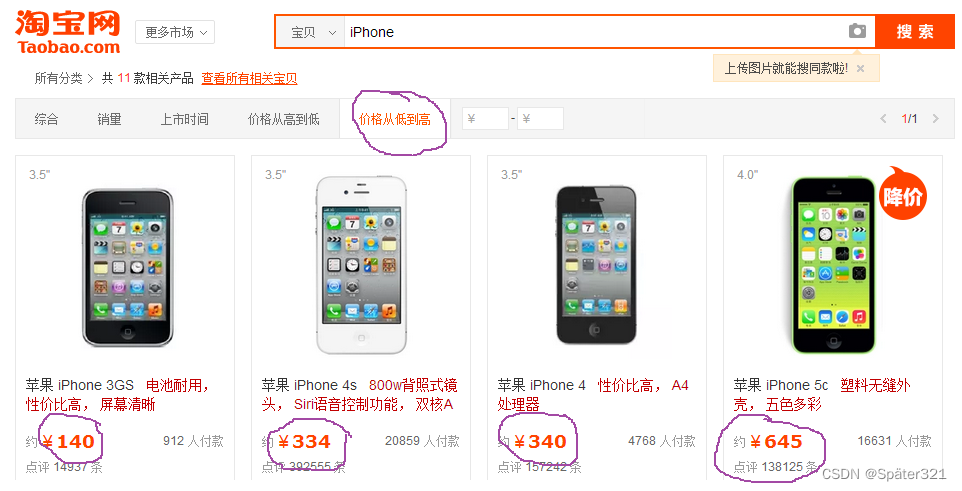
1.3、应用
1. 各大商城的价格从低到高等
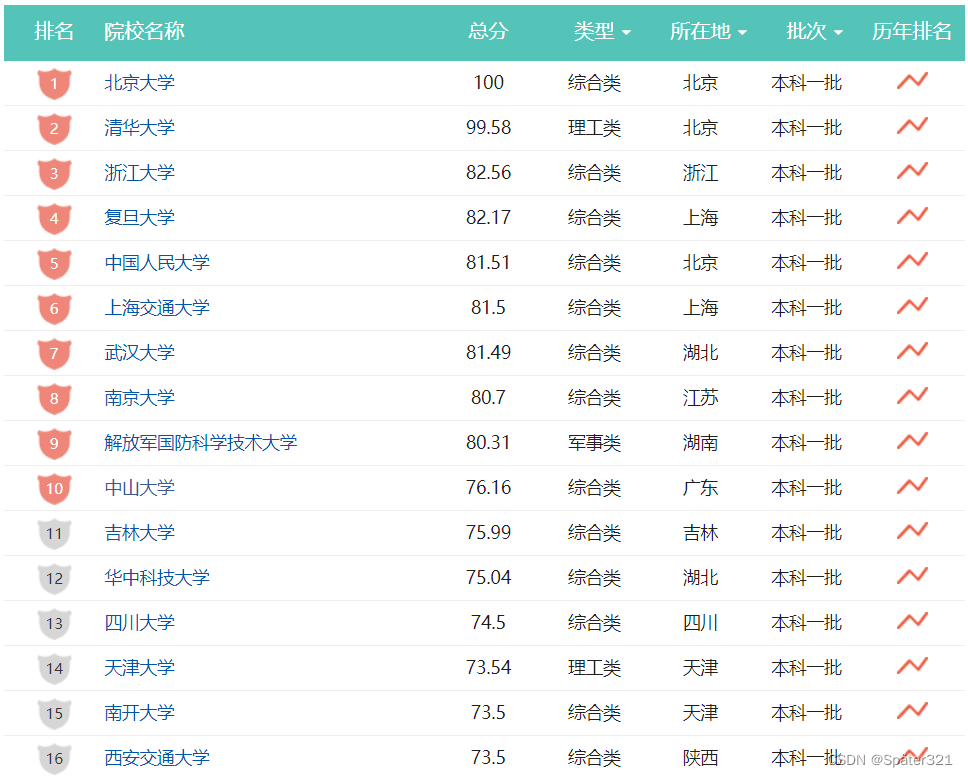
2. 中国大学排名
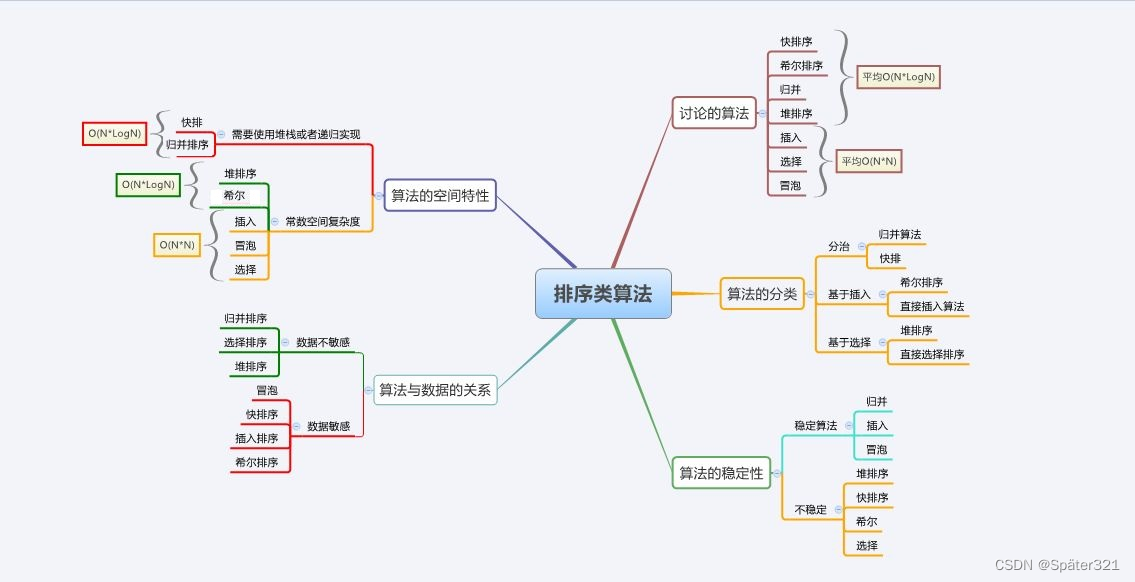
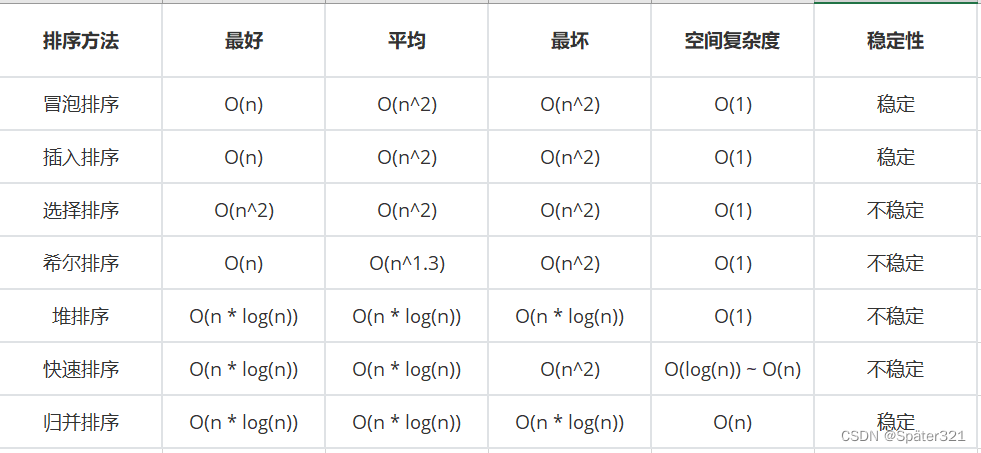
二、七大基于比较的排序-总览
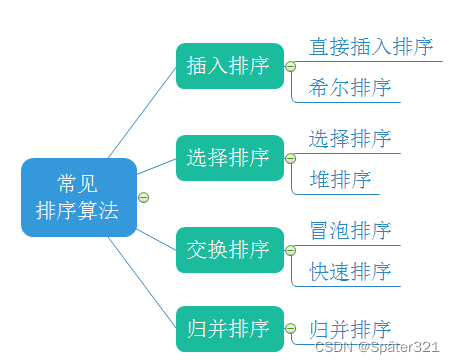
三、插入排序
3.1、直接插入排序-原理
整个区间被分为
- 有序区间
- 无序区间
每次选择无序区间的第一个元素,在有序区间内选择合适的位置插入
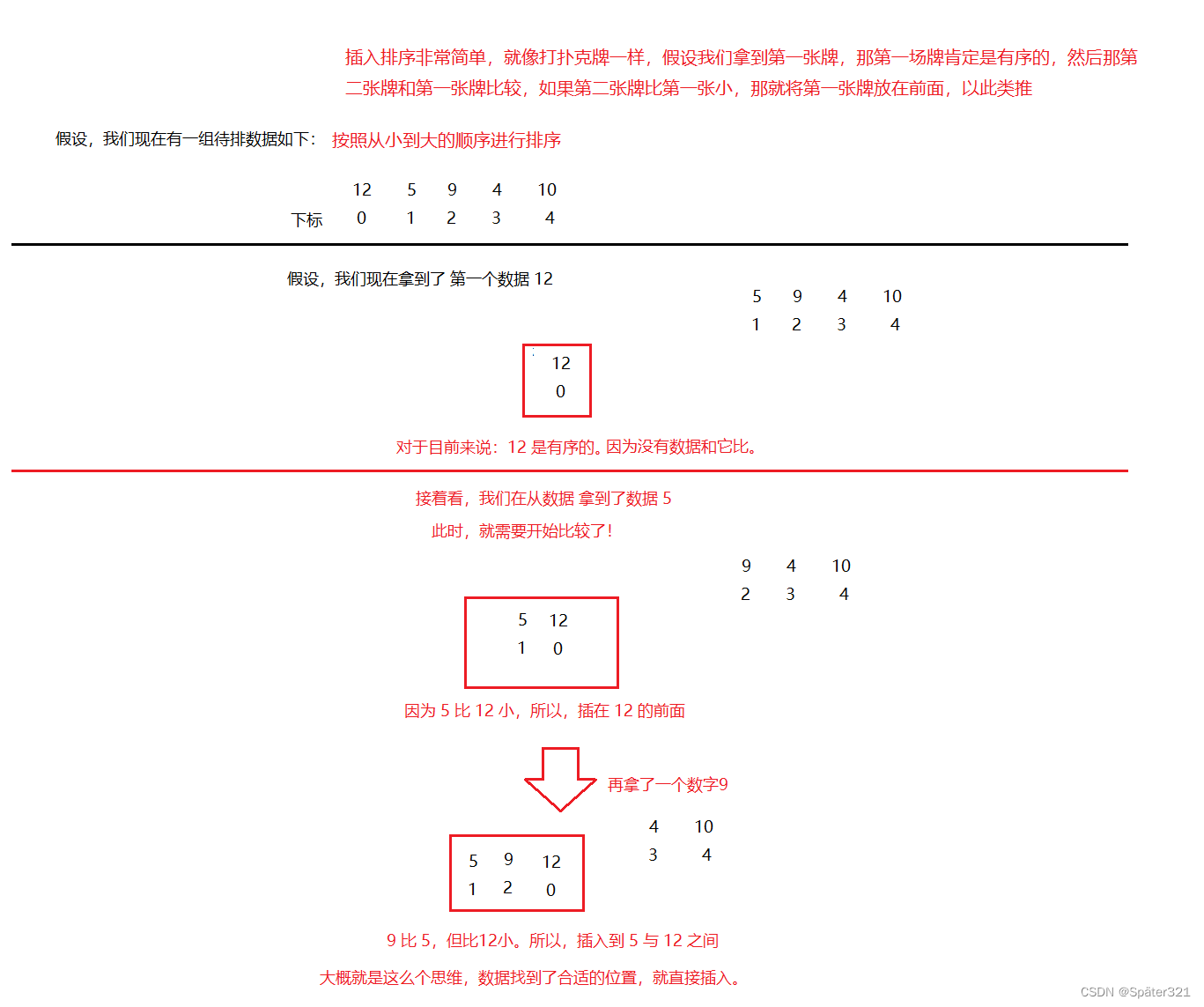
插入排序非常简单,就像打扑克牌一样,假设我们拿到第一张牌,那第一场牌肯定是有序的,然后那第二张牌和第一张牌比较,如果第二张牌比第一张小,那就将第一张牌放在前面,以此类推
根据这个思维:第一个数据是有序的,也就是说:在我们遍历的时候,是从下标1 开始的。
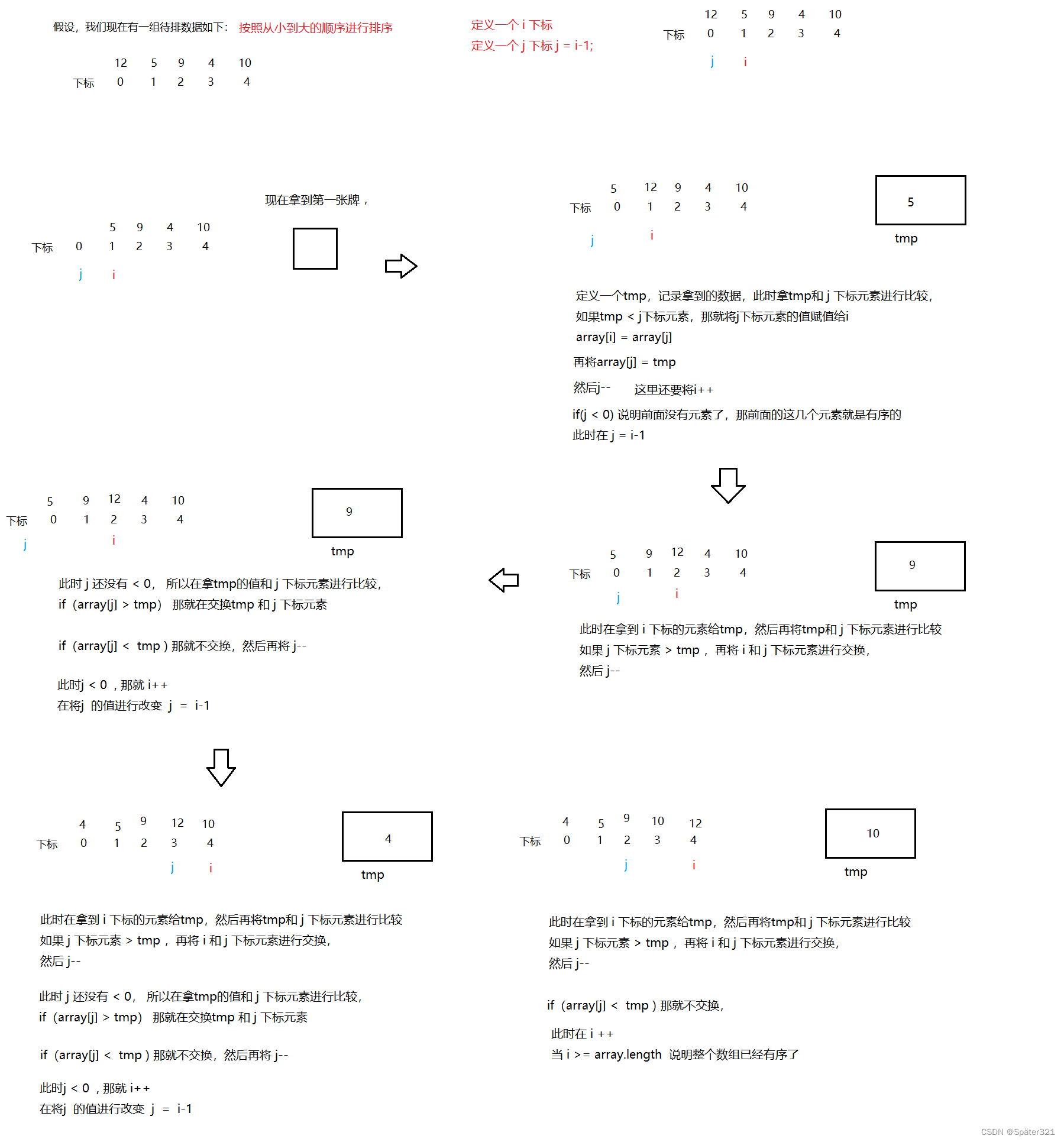
具体的操作见下图:
3.2、实现直接插入排序
/**
* 直接插入排序,按照从小到达的循序
* @param array
*/
public static void insertSortUp(int[] array){
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i-1;
for ( ;j >= 0; j--) {
if(array[j] > tmp){
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = tmp;
}
}
3.3、插入排序的性能分析
插入排序的稳定性:

结论
一个稳定的排序,可以实现为 不稳定的排序。 但是,一个本身就不稳定的排序是 无法变成 稳定的排序。
直接插入排序 是 有序的。 它的时间复杂度是 O(N^2);最好情况:O(N【数组有序】 也就是说:对于直接插入排序,数据越有序越快!
由此,不难联想到:直接插入排序有时候 会用于 优化 排序。
【假设:假设我们有一百万个数据需要排序,在排序的过程中,区间越来越小,数据越来越有序。直接插入排序的时间复杂度为 O(N),N
越来越小,那么,使用 直接插入排序是不是越来越快!也就是说:直接插入排序 有时候会 用于 排序优化】 直接插入排序经常使用在
数据量不多,且整体数据趋于有序的。
四、希尔排序
4.1、原理
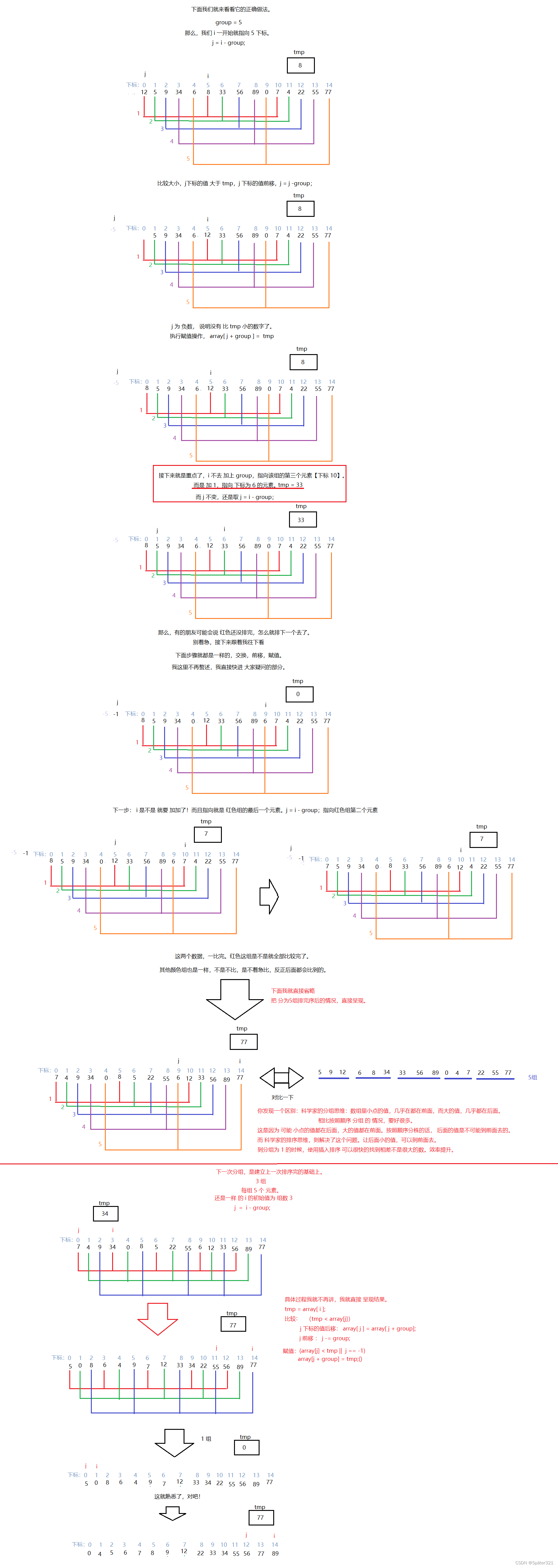
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数n,把待排序文件中所有记录分成n个组,所有距离为 (数据量/n) 的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达只有一个组时,所有记录在统一组内排好序。
- 希尔排序是对直接插入排序的优化。
- 当gap > 1(gap就是要分成的组数)时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很
快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比
正常情况下我们进行分组的时候都是按照顺序进行分组的
比如说:
那么,问题来了!我们怎去确定分多少组,而且越分越少。
【取自清华大学出版的一本书《数据结构》】
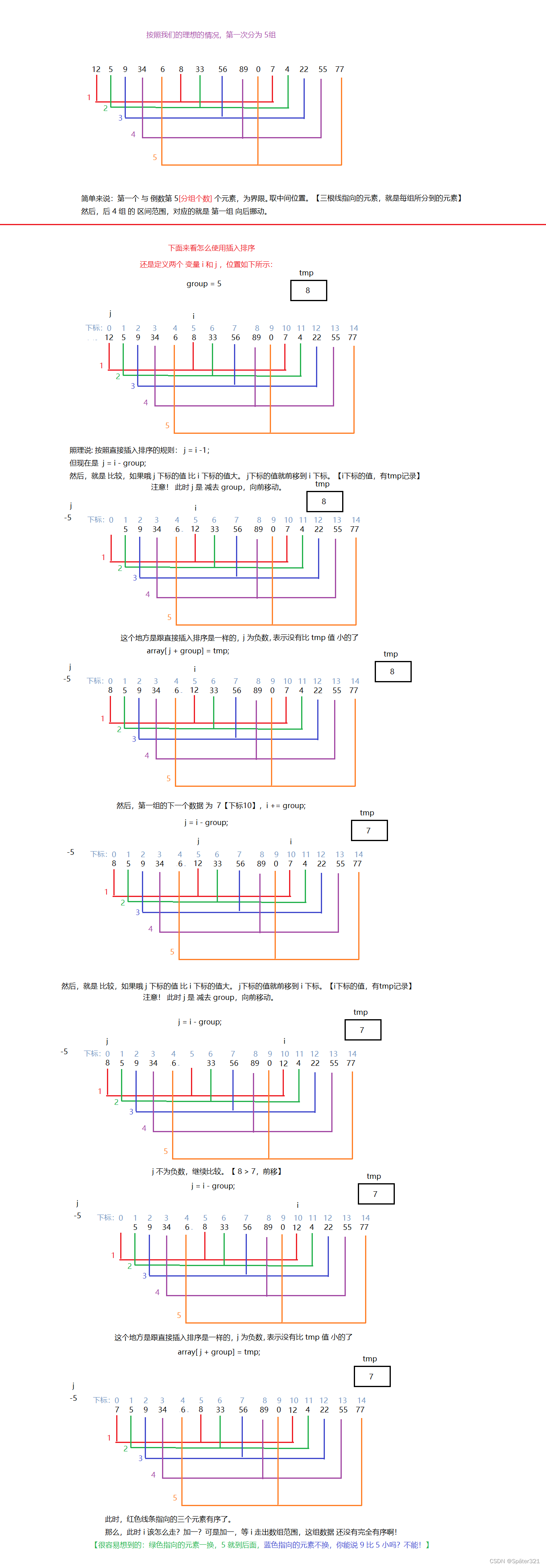
但是科学家的思维不同,他们分组的时候是跳着分组的
比如说:
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
4.2、模拟实现 - 希尔排序
/*
* 时间复杂度和增量有关系,所以无法得出准确的时间复杂度
* 但只需要记住:在一定的范围里,希尔排序的时间复杂度为 O(N^1.3 ~ N^1.5)
* 空间复杂度为 O(1)
* 稳定性:不稳定
* 判断稳定性的技巧:如果在比较的过程中 发生了 跳跃式交换。那么,就是不稳定的排序。
* */
public static void shell(int[] array,int group){
for (int i = group; i < array.length; i++) {
int j = i - group;
int tmp = array[i];
for( ; j >=0; j = j-group){
if(tmp < array[j]){
//交换元素
array[j+group] = array[j];
array[j] = tmp;
}else {
break;
}
}
array[j+group] = tmp;
}
}
public static void shellSort(int[] array){
//将整个数组分为5组
int gap = 5;
while(gap > 1){
//将分好组的数进行插入排序
shell(array, gap);
//循环得到分多少组,将分的组数按照 group / 2 来分组
gap = gap / 2;
}
//循环结束,那就说明前面分好组的数都排序好了,只剩下最后的一组 就是 gap = 1的组
shell(array, 1);
}
五、选择排序
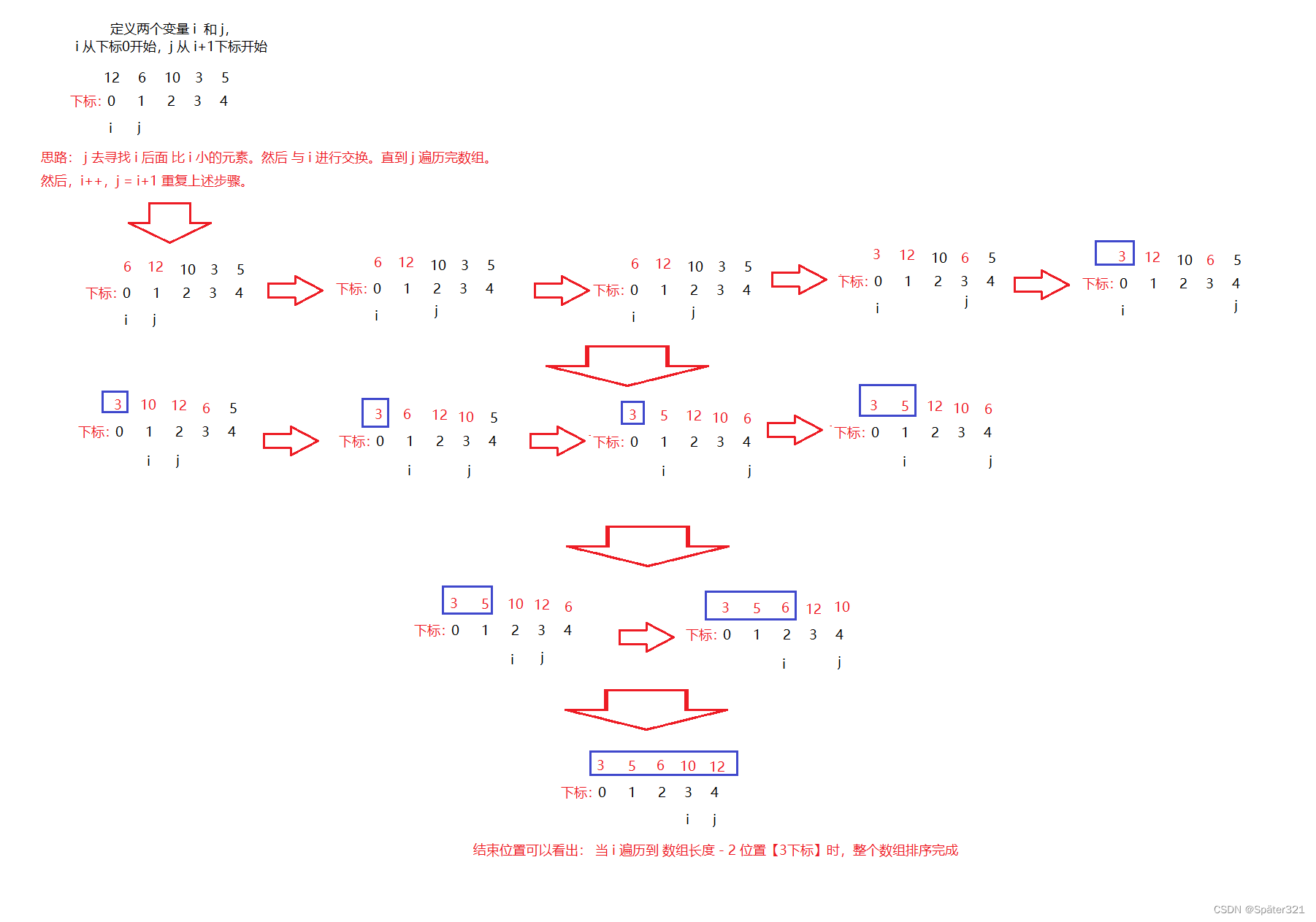
5.1、原理
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
优化
定义 一个 变量, 用来记录 此时的 i 后面最小值的下标。等 j 遍历完了,最小值的下标也就拿到了。此时,再进行交换。
这样就不必让上面那样,遇到比 i下标元素 小的,就交换。
5.2、模拟实现- 选择排序
/*
* 选择排序
* 稳定性: 不稳定 见附图
* 时间复杂度:O(N^2) 》》 外层循环 n -1,内层循环 n -1
* 空间复杂度:O(1)
* */
public static void selectSort(int[] array){
for (int i = 0; i < array.length; i++) {
for (int j = i+1; j < array.length; j++) {
if(array[i] > array[j]){
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
}
}
5.3、双向选择排序 (了解)
每一次从无序区间选出最小 + 最大的元素,存放在无序区间的最前和最后,直到全部待排序的数据元素排完 。
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
public static void selectSortOP(int[] array){
int low = 0;
int high = array.length - 1;
// [low,high] 表示整个无序区间
while(low < high){
int min = low;
int max = low;
for (int i = low+1; i <= high; i++) {
if(array[i] < array[min]){
min = i;
}
if(array[i] > array[max]){
max = i;
}
}
swap(array,min,low);
if(max == low){
max = min;
}
swap(array,max,high);
low++;
high--;
}
}
public static void swap(int[] array,int x,int y){
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}
六、堆排序
前面一篇文章讲过:Java -数据结构,【优先级队列 / 堆】
/**
* 堆排序
* @param array
*/
public static void heapSort(int[] array){
/*
* 时间复杂度:O(N * log2 N)
* 空间复杂度:O(1)
* 稳定性:不稳定
* */
int end = array.length - 1;
while(end>0){
int tmp = array[end];
array[end] = array[0];
array[0] = tmp;
shiftDown(array,0,end);
end--;
}
}
// 创建一个大根堆
public static void creMaxHeap(int[] arr){
for (int preant = (arr.length-1-1)/2; preant >= 0; preant--) {
shiftDown(arr,preant, arr.length);
}
}
/**
* 向下调整
* @param arr 数组
* @param preant 父亲节点的下标
* @param len 调整结束位置
*/
public static void shiftDown(int[] arr, int preant, int len){
int child = 2*preant+1;//孩子节点的下标
while (child < len){
if(child + 1 < len && arr[child] < arr[child+1]){
child = child+1;
}
if(arr[child] > arr[preant]){
int tmp = arr[child];
arr[child] = arr[preant];
arr[child] = tmp;
preant = child;
child = 2*preant+1;
}else {
break;
}
}
}
七、冒泡排序
/*
* 时间复杂度:O(N^2) 【无论是最好情况,还是最坏情况,时间复杂度都不变】
* 空间复杂度:O(1)
* 稳定性:稳定【未发生跳跃式交换】
* */
public static void bubbleSort(int[] array){
// 比较的趟数 = 数组的长度 - 1 【 0 ~ 3 一共 4趟】
for (int i = 0; i < array.length-1; i++) {
// 比较完一趟后,可以比较的元素个数减一。【因为靠后的数据已经有序】
// 内循环中,之所以要减一个 1,是因为防止 下面的if语句 发生 数组越界异常
for(int j = 0;j< array.length-1-i;j++){
if(array[j] > array[j+1]){
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
}
}
}
}
八、快速排序 - 重点
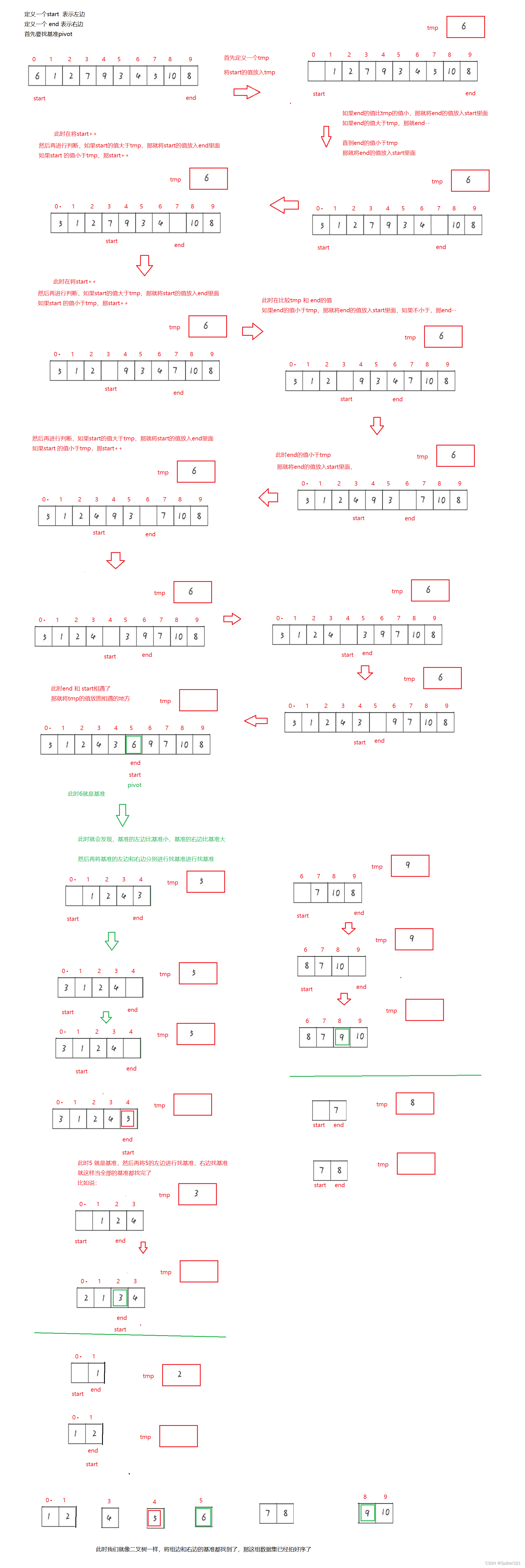
8.1、原理
- 从待排序区间选择一个数,作为基准值(pivot);
- Partition: 遍历整个待排序区间,将比基准值小的(可以包含相等的)放到基准值的左边,将比基准值大的(可以包含相等的)放到基准值的右边;
- 采用分治思想,对左右两个小区间按照同样的方式处理,直到小区间的长度 == 1,代表已经有序,或者小区间的长度 == 0,代表没有数据。
总结
快速排序,其实说白了 和 二叉树 很像,先根,再左,后右。利用递归去实现!
8.2、模拟实现 - 快速排序
/**
* 快速排序 - 将这组数据从小到大排序
* 时间复杂度:O(N^2) 【数据有序或者逆序的情况】
* 最好情况【每次可以均匀的分割待排序序列】:O(N * log2 N)
* 空间复杂度:O(N)[单分支的一棵树]
* 最好:log2 N
* 稳定性:不稳定
* @param array
*/
public static void quickSort(int[] array){
quick(array,0,array.length-1);
}
//排序
public static void quick(int[] array, int left, int right){
//排序
if(left >= right){
return;
}
//找基准
int pivot = partition(array,left, right);
quick(array,left,pivot-1);
quick(array,pivot+1,right);
}
/**
* 找基准
*/
public static int partition(int[] array, int start, int end){
int tmp = array[start];
while (start < end){
while (start < end && array[end] >= tmp){
end--;
}
array[start] = array[end];
while (start < end && array[start] <= tmp){
start++;
}
array[end] = array[start];
}
array[start] = tmp;
return start;
}
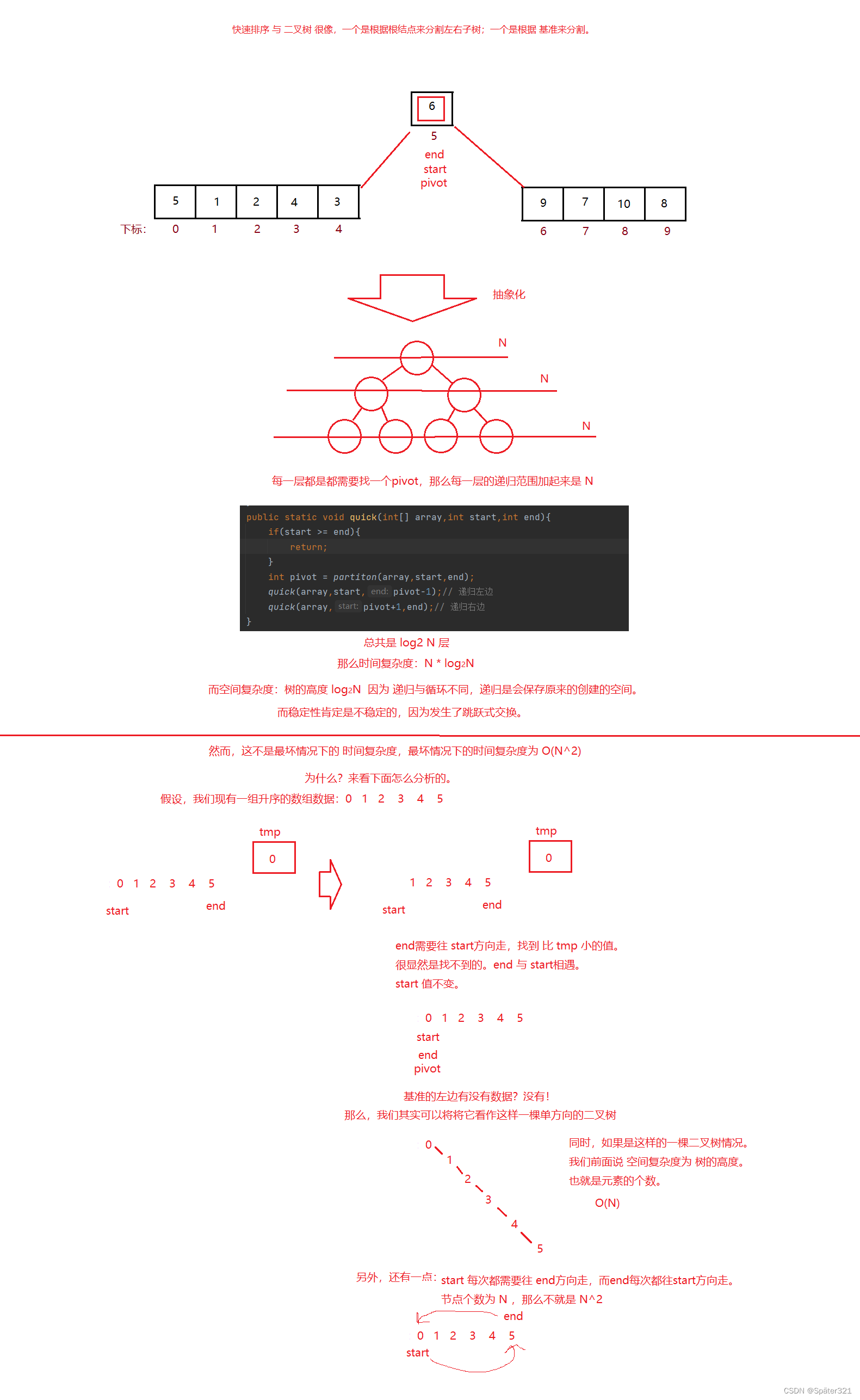
8.3、快速排序 的 时间 与 空间复杂度分析
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
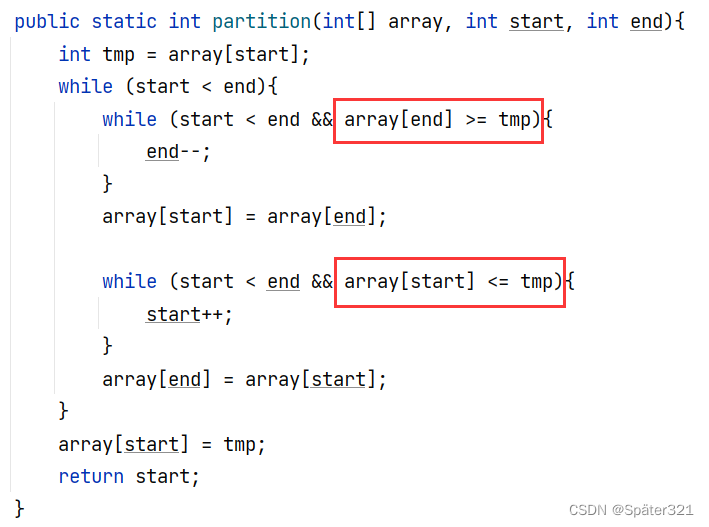
细节拓展
if语句中 比较大小的代码中 等号是不能省略的
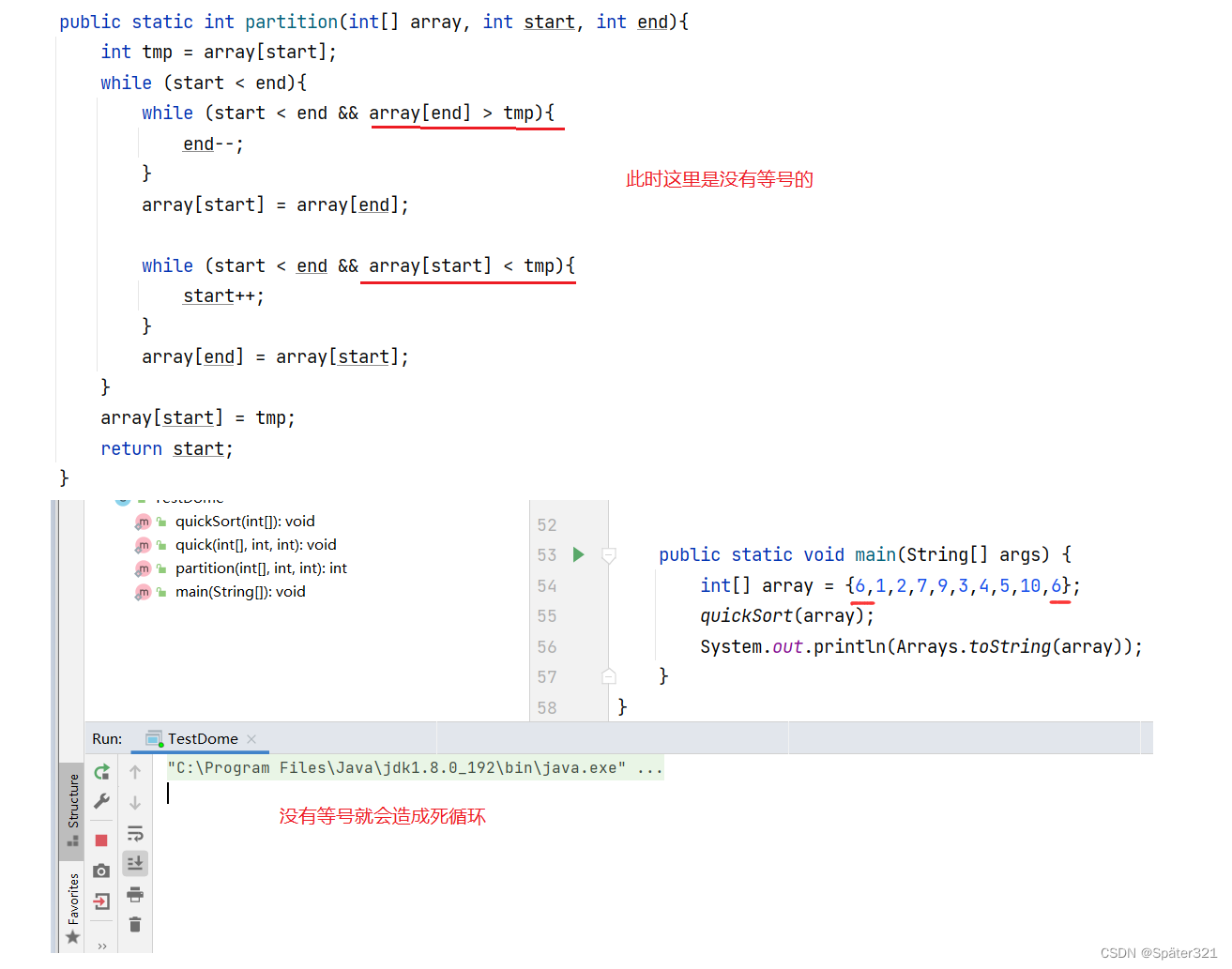
当 下面框选的代码 没有等号时,会造成死循环。
我就改了一下,末尾元素的值。
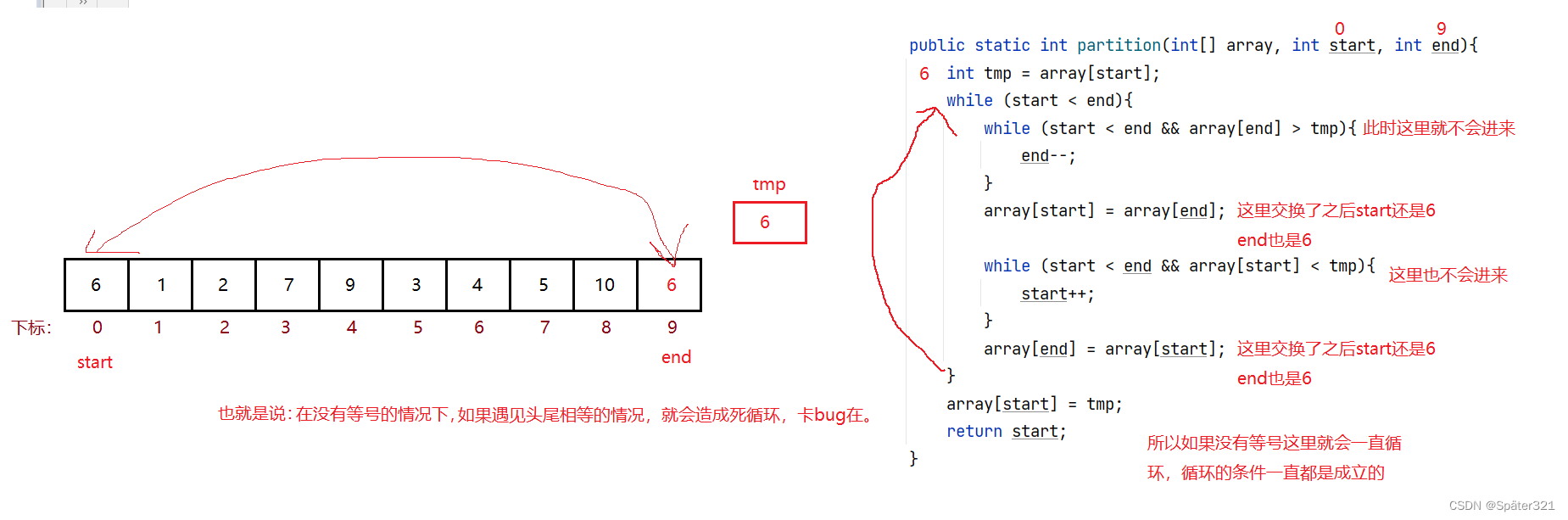
那么,问题来了:为什么没有等号就死循环了?
所以,在 写快排的时候,比较大小的代码,记住一定要加上等号!!!!!
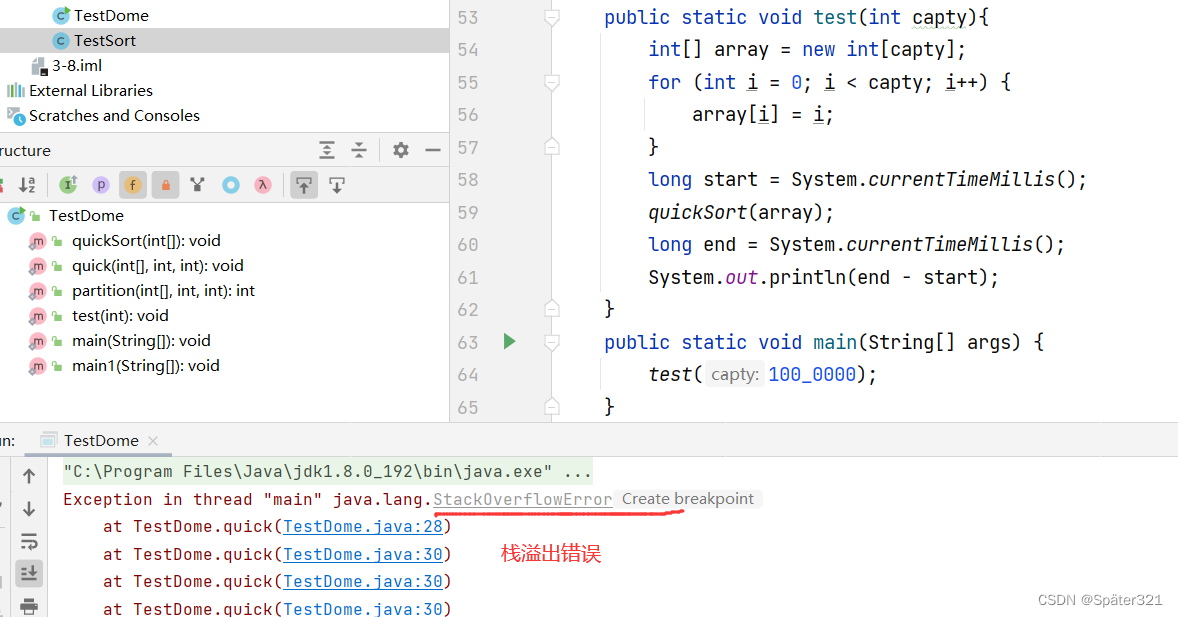
目前版本的 快排代码 不支持 大量数据进行排序 - 会导致栈溢出。
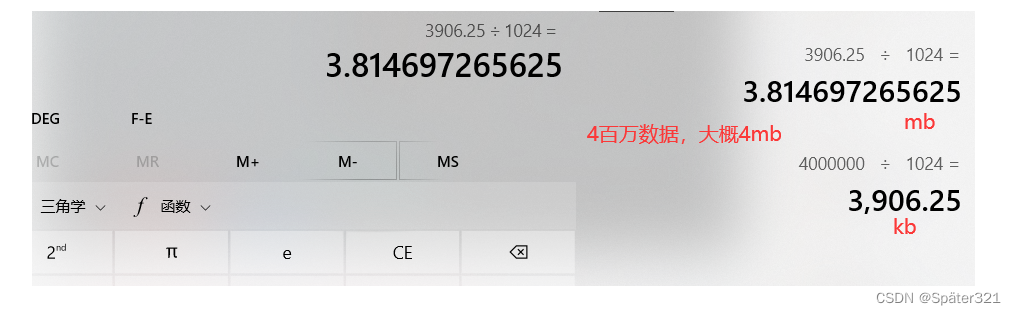
这是因为 我们递归的太深了,1百万数据,4百万字节。 1TB等于1024GB;1GB等于1024MB;1MB等于1024KB;1KB等于1024Byte(字节);1Byte等于8bit(位);
有的朋友会说:这才多大啊?栈怎么会被挤爆? 这是因为在递归的时候,开辟的栈帧【函数的信息,参数等等等…都有】,所以,每次开辟的栈帧不止 4byte。故栈被挤爆了。
所以,我们要优化快排的 代码。【优化:数据有序的情况】
基准值的选择 - 优化前的知识补充
1、选择边上(左或者右) 【重点,上面使用的就是这种方法】
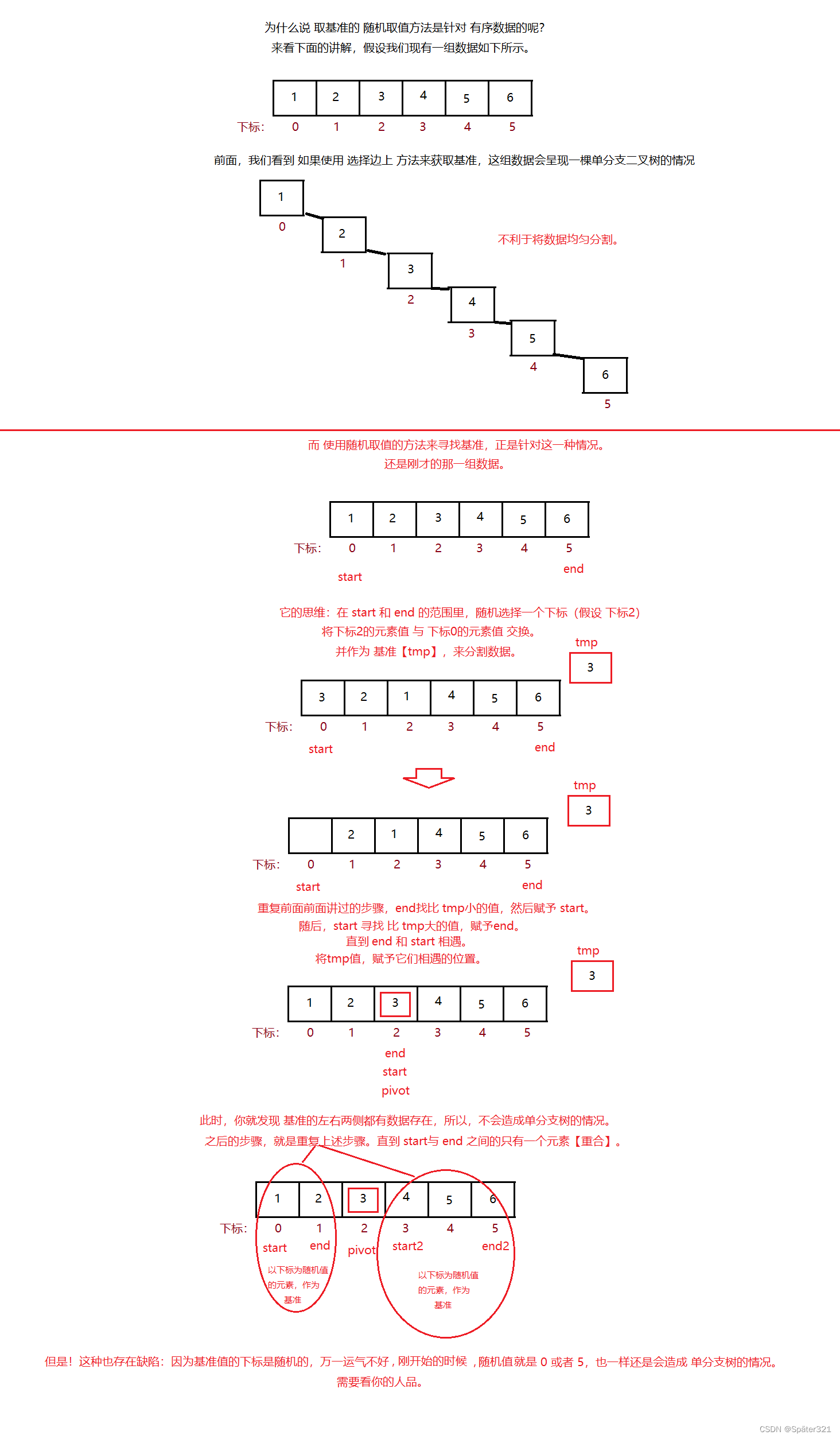
2、随机选择(针对 有序数据)【了解】
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
/*
* 时间复杂度:O(N^2) 【数据有序或者逆序的情况】
* 最好情况【每次可以均匀的分割待排序序列】:O(N * log2 N)
* 空间复杂度:O(N)[单分支情况]
* 最好:log2 N
* 稳定性:不稳定
* */
public static void quickSort(int[] array){
quick(array,0, array.length-1);
}
public static void quick(int[] array,int start,int end){
if(start >= end){
return;
}
// 在找基准之前,先确定 start 和 end 的 中间值。[三数取中法]
int midValIndex = findMidValIndex(array,start,end);
//将它 与 start 交换。这样后面的程序,就不用改动了。
swap(array,start,midValIndex);
int pivot = partiton(array,start,end);
quick(array,start,pivot-1);// 递归左边
quick(array,pivot+1,end);// 递归右边
}
// 确定基准值下标
private static int findMidValIndex(int[] array,int start,int end){
// 确定 start 和 end 的中间下标
int mid = start + ((end - start)>>>1);// == (start + end)/ 2
// 确定 mid、start、end 三个下标,谁指向的元素是三个元素中的中间值
if(array[end] > array[start]){
if(array[start] > array[mid]){
return start;
}else if(array[mid] > array[end]){
return end;
}else{
return mid;
}
}else{
// array[start] >= array[end]
if(array[end] > array[mid]){
return end;
}else if(array[mid] > array[start]){
return start;
}else {
return mid;
}
}
}
// 交换两个下标元素
private static void swap(int[] array,int x,int y){
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}
// 分割 - 找基准
private static int partiton(int[] array,int start,int end){
int tmp = array[start];
while(start < end){
while(start < end && array[end] >= tmp){
end--;
}
// 此时 end 下标 元素的值 是 小于 tmp的。
array[start] = array[end];
while(start<end && array[start] <= tmp){
start++;
}
array[end] = array[start];
}
array[start] = tmp;
return start;
}
8.4、快速排序 - 非递归实现
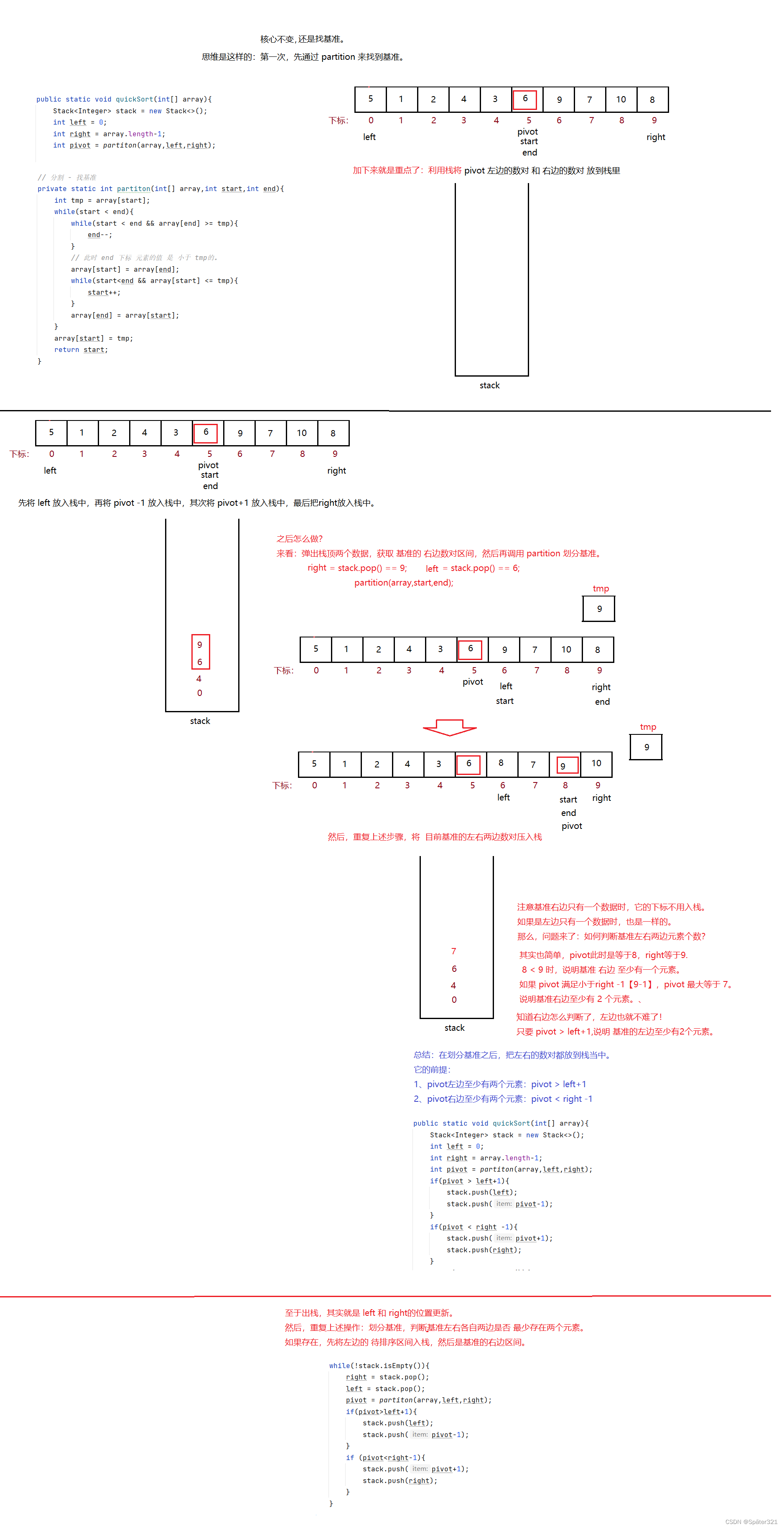
public static void quickSort(int[] array){
Stack<Integer> stack = new Stack<>();
int left = 0;
int right = array.length-1;
int pivot = partiton(array,left,right);
if(pivot > left+1){
stack.push(left);
stack.push(pivot-1);
}
if(pivot < right -1){
stack.push(pivot+1);
stack.push(right);
}
while(!stack.isEmpty()){
right = stack.pop();
left = stack.pop();
pivot = partiton(array,left,right);
if(pivot>left+1){
stack.push(left);
stack.push(pivot-1);
}
if (pivot<right-1){
stack.push(pivot+1);
stack.push(right);
}
}
}
// 分割 - 找基准
private static int partiton(int[] array,int start,int end){
int tmp = array[start];
while(start < end){
while(start < end && array[end] >= tmp){
end--;
}
// 此时 end 下标 元素的值 是 小于 tmp的。
array[start] = array[end];
while(start<end && array[start] <= tmp){
start++;
}
array[end] = array[start];
}
array[start] = tmp;
return start;
}
九、归并排序 - 重点
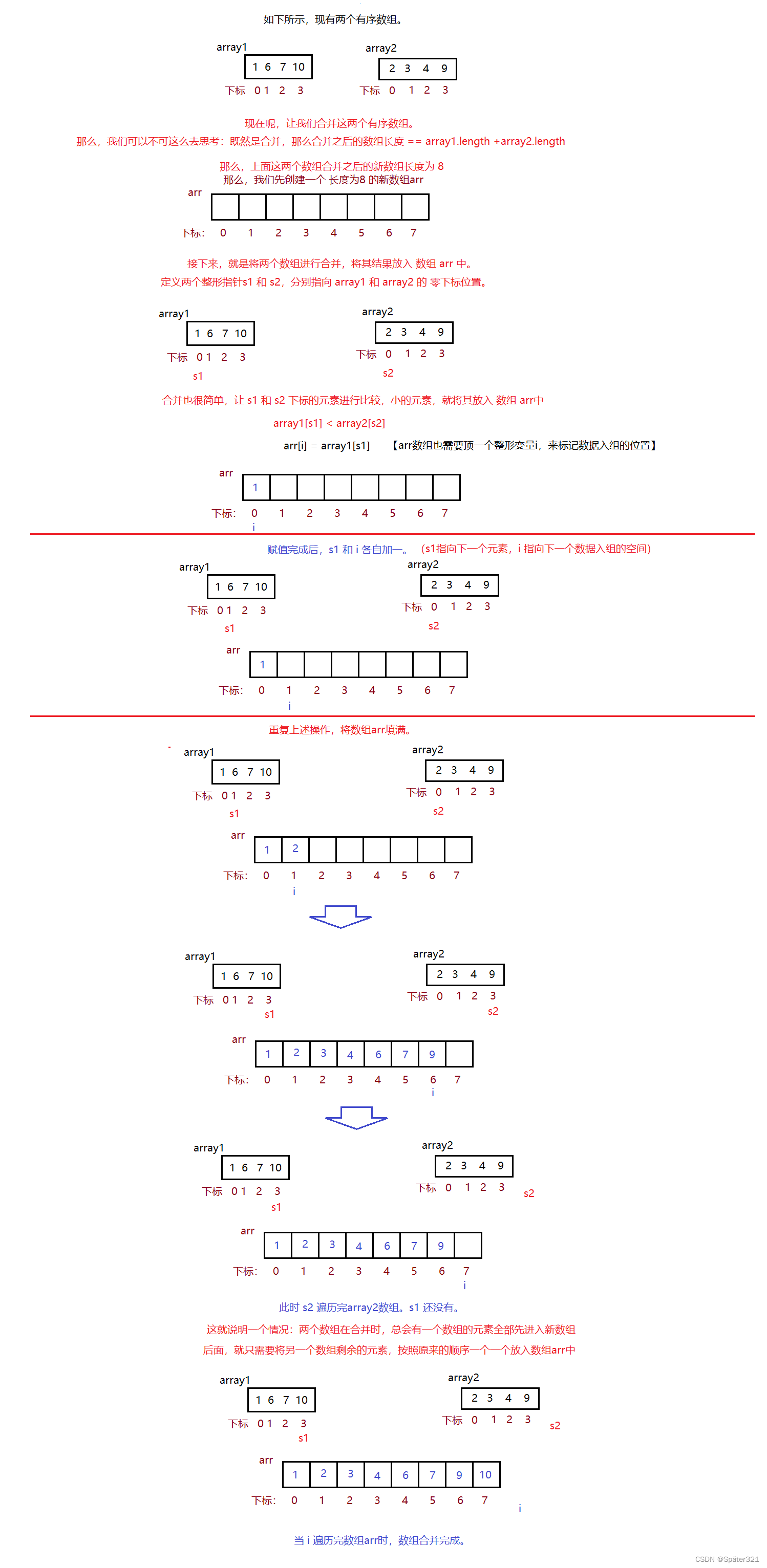
首先做一个题:将两个有序表合并成一个有序表,称为二路归并。【简单说就是 将两个有序数组合并为一个有序数组,称为二路合并】
//二路合并的代码如下
public static int[] mergeArrays(int[] array1,int[] array2){
if(array1 == null || array2 == null){
return array1 == null ? array2: array1;
}
int[] arr = new int[array1.length + array2.length];
int i = 0;// arr 的 遍历变量
int s1 = 0;//array1 的 遍历变量
int s2 = 0;//array2 的 遍历变量
while(s1 < array1.length && s2 < array2.length){
if(array1[s1] > array2[s2]){
arr[i++] = array2[s2++];
// s2++;
// i++;
}else{
arr[i++] = array1[s1++];
// s1++;
// i++;
}
}
// 循环结束,有一个数组的元素已经全部存入
// 接下来就是将另一个数组的元素放入 arr 中
while (s1 < array1.length){
arr[i++] = array1[s1++];
// i++;
// s1++;
}
while (s2 < array2.length){
arr[i++] = array2[s2++];
// i++;
// s2++;
}
return arr;
}
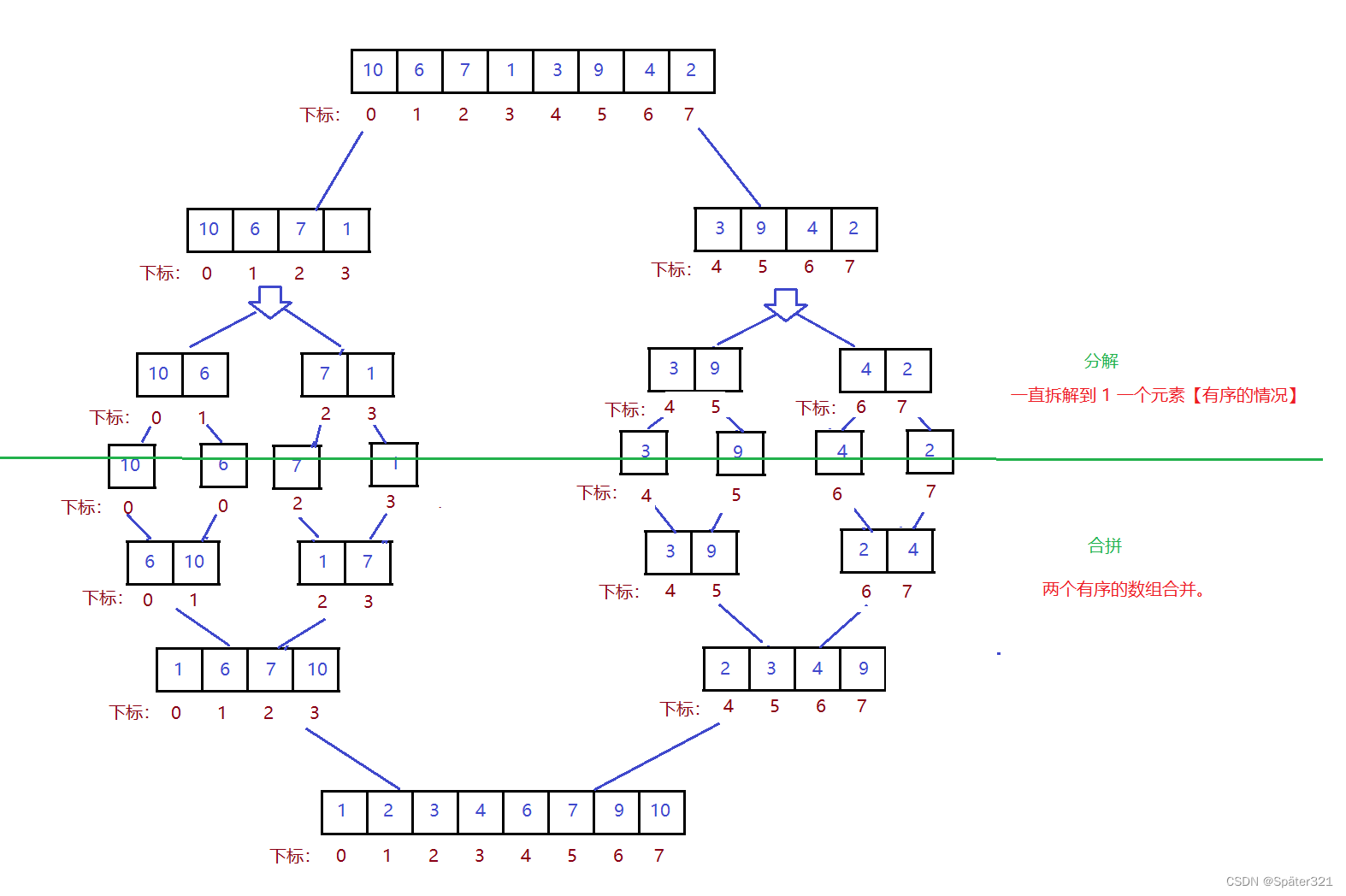
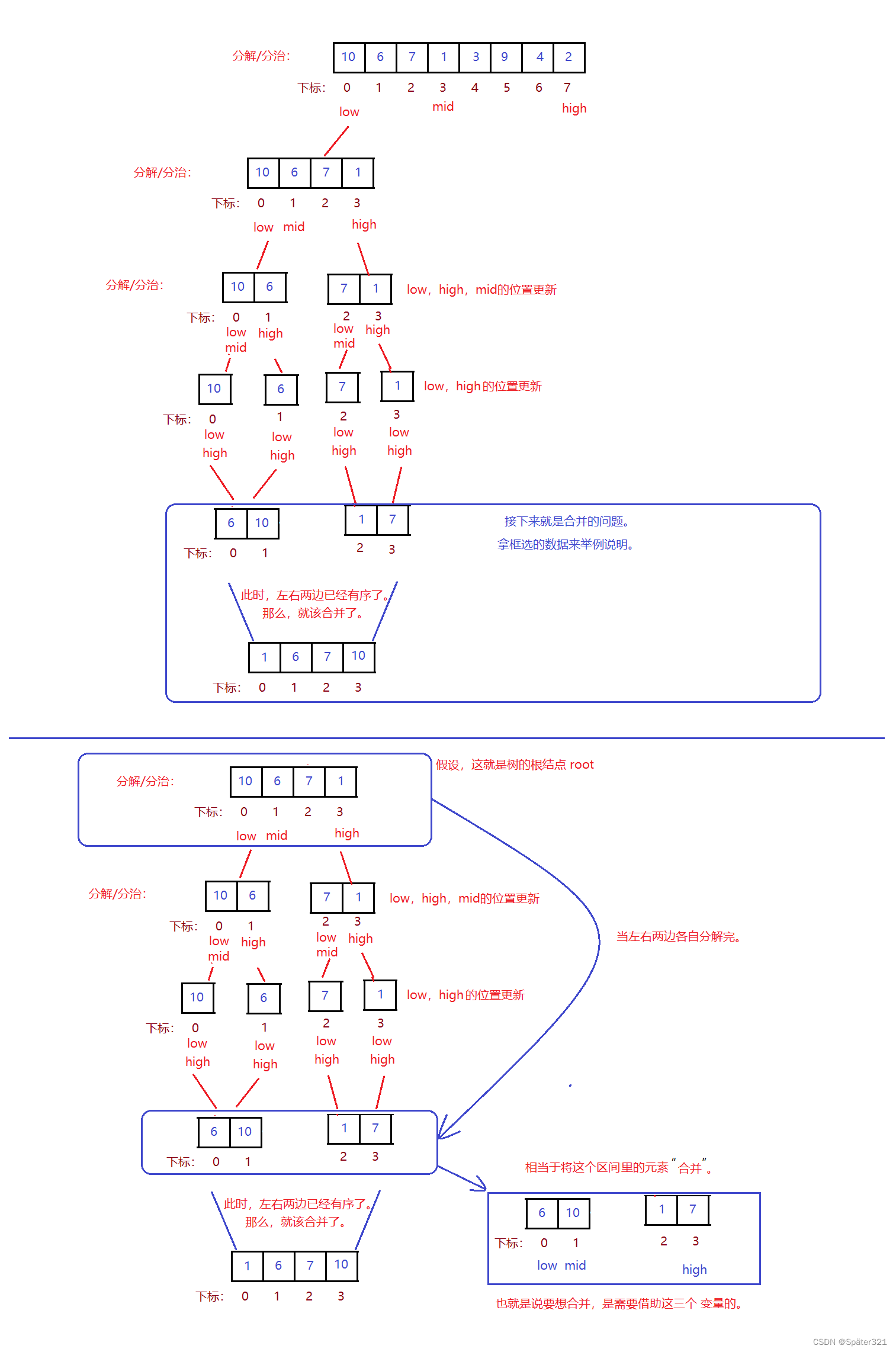
9.1、归并排序 - 原理
归并排序(MERGE - SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
难点1 - 如何将一个数组拆分成一个个单独数组【每个数组里只包含一个元素】。
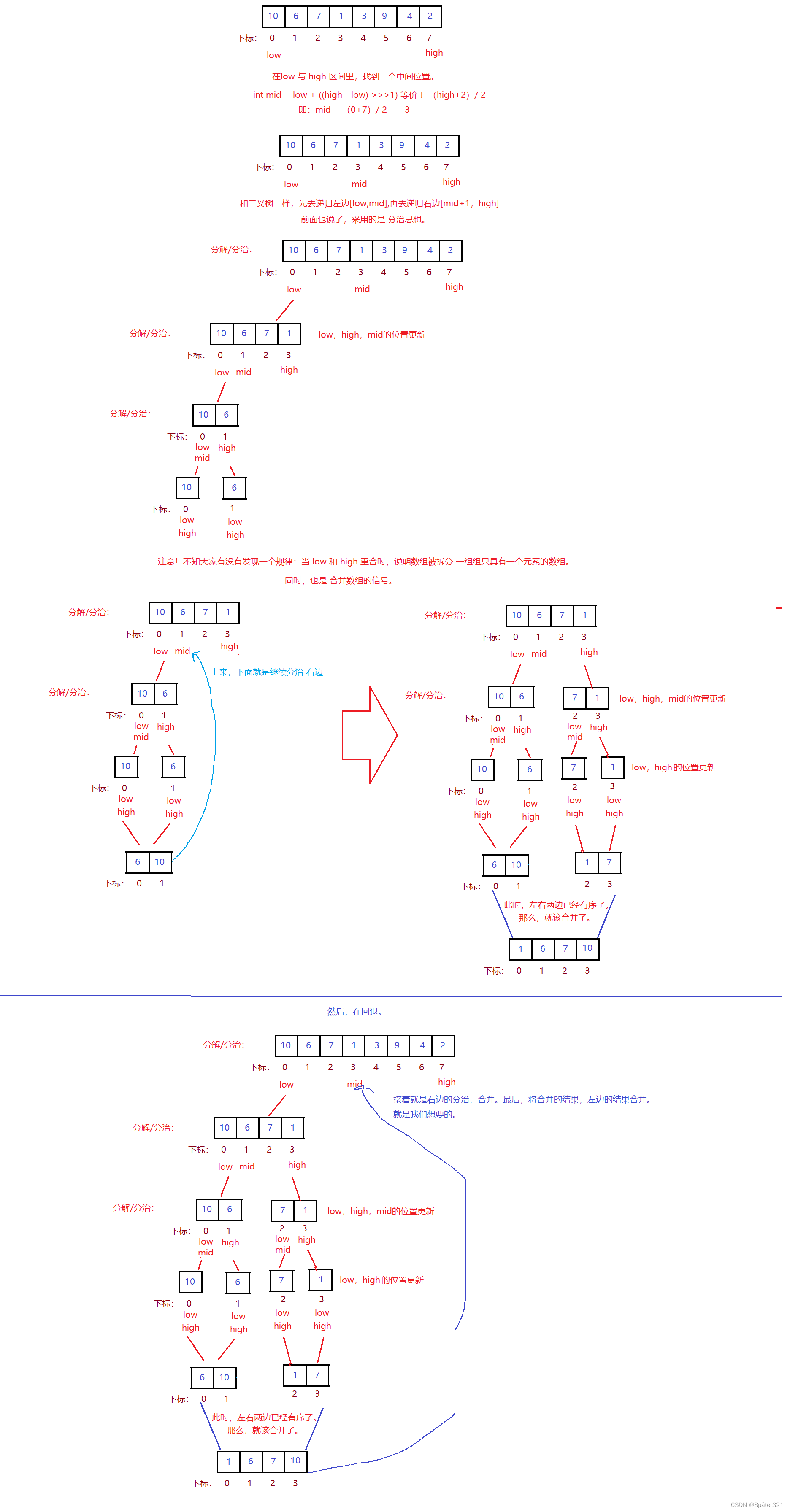
难点2 - 合并
总程序
/*
* 时间复杂度:N * log2 N
* 空间复杂丢:O(N)
* 稳定性:稳定
* */
public static int[] mergeSort(int[] array){
if(array == null){
return array;
}
mergeSortFunc(array,0,array.length-1);
return array;
}
private static void mergeSortFunc(int[] array,int low,int high){
if(low >= high){
return;
}
// int mid = (high + low) >>> 1
int mid = low + ((high - low) >>> 1);
mergeSortFunc(array,low,mid);// 左边
mergeSortFunc(array,mid+1,high);// 右边
merge(array,low,mid,high);
}
private static void merge(int[] array,int low,int mid,int high){
int[] arr = new int[high - low +1];
int start1 = low;
int end1 = mid;
int start2 = mid+1;
int end2 = high;
int i = 0;
while (start1 <= end1 && start2 <= end2){
if(array[start1] > array[start2]){
arr[i++] = array[start2++];
}else{
arr[i++] = array[start1++];
}
}
while(start1 <= end1){
arr[i++] = array[start1++];
}
while(start2 <= end2){
arr[i++] = array[start2++];
}
for (int j = 0; j < arr.length; j++) {
array[low++] = arr[j];
}
}
归并排序 - 时间与空间复杂度分析、稳定性

9.2、归并排序 - 非递归实现
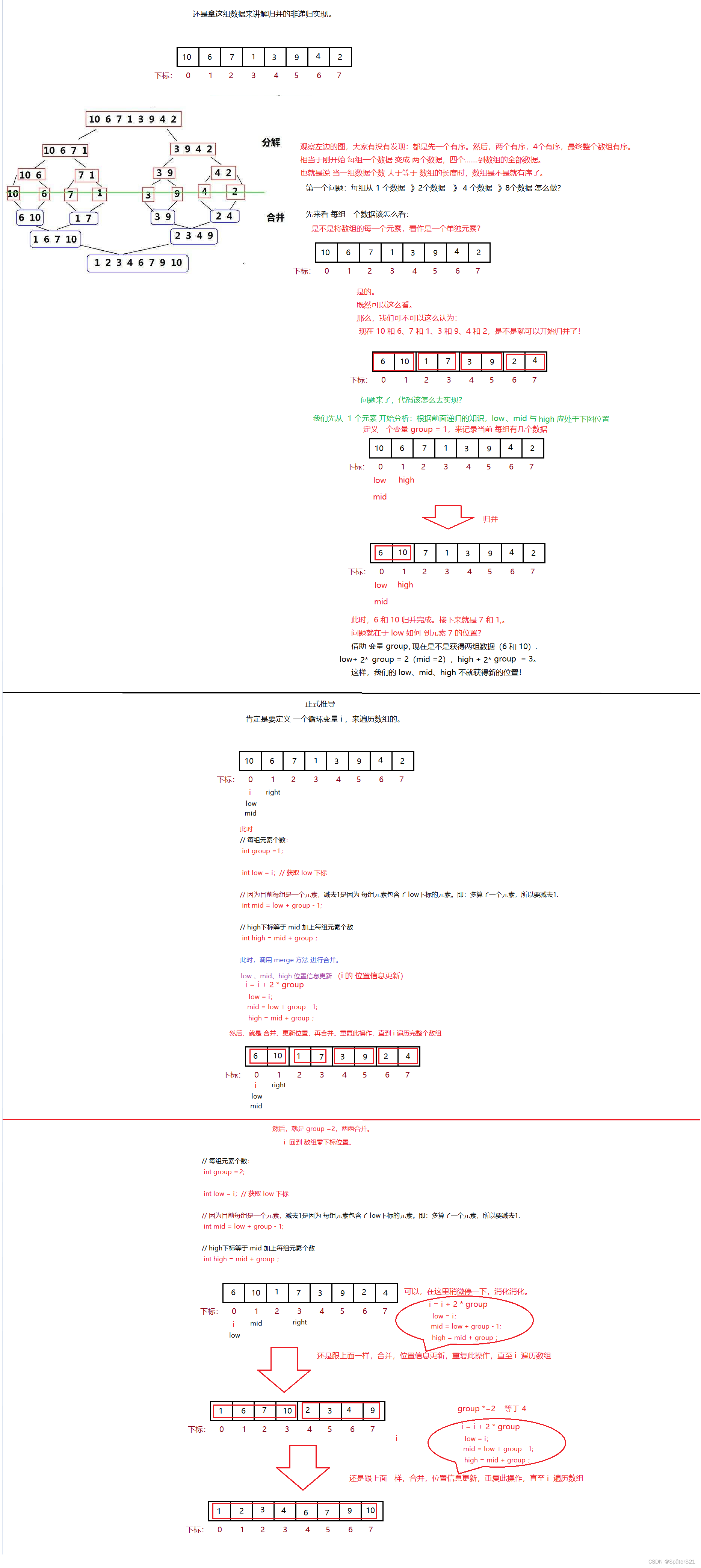
public static void mergeSort(int[] array){
//归并排序非递归实现
int groupNum = 1;// 每组的数据个数
while(groupNum < array.length){
// 无论数组含有几个元素, 数组每次都需要从下标 0位置,开始遍历。
for(int i = 0;i<array.length;i+= groupNum * 2){
int low = i;
int mid = low + groupNum -1;
// 防止越界【每组的元素个数,超过了数组的长度】
if(mid >= array.length){
mid = array.length-1;
}
int high = mid + groupNum;
// 防止越界【超过了数组的长度】
if(high >= array.length){
high = array.length-1;
}
merge(array,low,mid,high);
}
groupNum *= 2;//每组的元素个数扩大到原先的两倍。
}
}
public static void merge(int[] array,int low,int mid,int high){
// high 与 mid 相遇,说明 此时数组分组只有一组,也就说没有另一组的数组与其合并
// 即数组已经有序了,程序不用再往下走。
if(high == mid){
return;
}
int[] arr = new int[high -low + 1];
int start1 = low;
int end1 = mid;
int start2 = mid+1;
int end2 = high;
int i = 0;
while(start1 <= end1 && start2 <= end2){
if(array[start1]>array[start2]){
arr[i++] = array[start2++];
}else{
arr[i++] = array[start1++];
}
}
while (start1 <= end1){
arr[i++] = array[start1++];
}
while(start2 <= end2){
arr[i++] = array[start2++];
}
for (int j = 0; j < arr.length; j++) {
array[low++] = arr[j];
}
}
海量数据的排序问题
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 200 路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
十、排序总结