时序差分方法
- Temporal Difference Learning
- 举个例子
- TD learning of state values
- 算法描述
- TD learning of action values: Sarsa
- TD learning of action values: Expected Sarsa
- TD learning of action values: n-step Sarsa
- TD learning of optimal action values: Q-learning
- A unified point of view
- Summary
- 内容来源
Temporal Difference Learning
本文主要介绍temporal-difference(TD) learning,这是一个在强化学习领域比较知名的方法。Monte Carlo(MC)learning是第一种model-free方法,TD learning是第二种model-free方法。与MC方法相比,TD算法有很多优势。本文我们将研究如何将stochastic approximate methods应用于TD learning。
举个例子
首先,考虑一个简单的mean estimation问题:计算
w
=
E
[
X
]
w=\mathbb{E}[X]
w=E[X]基于
X
X
X的一些iid采样
{
x
}
\{x\}
{x}。
求解过程:
- 将上式重写为 g ( w ) = w − E [ X ] g(w)=w-\mathbb{E}[X] g(w)=w−E[X],我们可以将问题reformulate为一个root-finding问题 g ( w ) = 0 g(w)=0 g(w)=0
- 因为我们仅能获得 X X X中的一些采样 { x } \{x\} {x},那么观察到的噪声表示为 g ~ ( w , η ) = w − x = ( w − E [ X ] ) + ( E [ X ] − x ) ≐ g ( w ) + η \tilde{g}(w, \eta)=w-x=(w-\mathbb{E}[X])+(\mathbb{E}[X]-x)\doteq g(w)+\eta g~(w,η)=w−x=(w−E[X])+(E[X]−x)≐g(w)+η
- 根据之前的RM算法求解 g ( w ) = 0 g(w)=0 g(w)=0,即 w k + 1 = w k − α k g ~ ( w k , η k ) = w k − α k ( w k − x k ) w_{k+1}=w_k-\alpha_k\tilde{g}(w_k, \eta_k)=w_k-\alpha_k(w_k-x_k) wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−xk)
然后,考虑一个稍微复杂的问题。估计一个函数
v
(
X
)
v(X)
v(X)的mean:$
w
=
E
[
v
(
X
)
]
w=\mathbb{E}[v(X)]
w=E[v(X)]基于
X
X
X的一些iid采样
{
x
}
\{x\}
{x}。
求解过程:
- 首先定义 g ( w ) = w − E [ v ( X ) ] g(w)=w-\mathbb{E}[v(X)] g(w)=w−E[v(X)],然后 g ~ ( w , η ) = w − v ( x ) = ( w − E [ v ( X ) ] ) + ( E [ v ( X ) ] − v ( x ) ) ≐ g ( w ) + η \tilde{g}(w, \eta)=w-v(x)=(w-\mathbb{E}[v(X)])+(\mathbb{E}[v(X)]-v(x))\doteq g(w)+\eta g~(w,η)=w−v(x)=(w−E[v(X)])+(E[v(X)]−v(x))≐g(w)+η
- 然后问题变为 g ( w ) = 0 g(w)=0 g(w)=0的求根问题,对应的RM算法是 w k + 1 = w k − α k g ~ ( w k , η k ) = w k − α k ( w k − v ( x k ) ) w_{k+1}=w_k-\alpha_k\tilde{g}(w_k, \eta_k)=w_k-\alpha_k(w_k-v(x_k)) wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−v(xk))
再看一个例子,考虑一个更加复杂的问题。计算
w
=
E
[
R
+
γ
v
(
X
)
]
w=\mathbb{E}[R+\gamma v(X)]
w=E[R+γv(X)]其中
R
,
X
R,X
R,X是随机变量,
γ
\gamma
γ是一个常数,
v
(
⋅
)
v(\cdot)
v(⋅)是一个函数.
求解过程:
- 假设我们可以获得 X X X和 R R R的采样 { x } \{x\} {x}和 { r } \{r\} {r},定义 g ( w ) = w − E [ R + γ v ( X ) ] g(w)=w-\mathbb{E}[R+\gamma v(X)] g(w)=w−E[R+γv(X)],然后 g ~ ( w , η ) = w − ( r + γ v ( x ) ) = ( w − E [ R + γ v ( X ) ] ) + ( E [ R + γ v ( X ) ] − ( r + γ v ( x ) ) ) ≐ g ( w ) + η \tilde{g}(w, \eta)=w-(r+\gamma v(x))=(w-\mathbb{E}[R+\gamma v(X)])+(\mathbb{E}[R+\gamma v(X)]-(r+\gamma v(x)))\doteq g(w)+\eta g~(w,η)=w−(r+γv(x))=(w−E[R+γv(X)])+(E[R+γv(X)]−(r+γv(x)))≐g(w)+η
- 然后问题变成了 g ( w ) = 0 g(w)=0 g(w)=0的求根问题,那么对应的RM算法是 w k + 1 = w k − α k g ~ ( w k , η k ) = w k − α k ( w k − ( r k + γ v ( x k ) ) ) w_{k+1}=w_k-\alpha_k\tilde{g}(w_k, \eta_k)=w_k-\alpha_k(w_k-(r_k+\gamma v(x_k))) wk+1=wk−αkg~(wk,ηk)=wk−αk(wk−(rk+γv(xk)))
小结一下, 上面三个例子越来越复杂,但是都可以通过RM算法进行求解。
TD learning of state values
TD learning既可以指一大类的强化学习算法,也可以指一个具体的estimating state values的算法。TD算法是基于数据,也就是不基于模型来实现强化学习。
算法描述
TD算法要求的data/experience如下:

The TD learning algorithm如下:
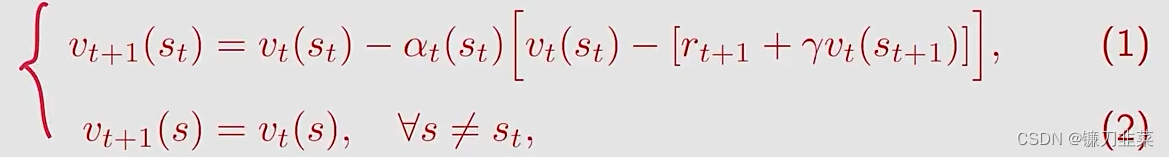
其中
t
=
0
,
1
,
2
,
.
.
.
t=0,1,2,...
t=0,1,2,...,这里的
v
t
(
s
t
)
v_t(s_t)
vt(st)是
v
π
(
s
t
)
v_\pi (s_t)
vπ(st)的estimated state value,s是state space,
α
t
(
s
t
)
\alpha_t(s_t)
αt(st)是在
t
t
t时刻
s
t
s_t
st的学习率。
- 在t时刻,只有visited state s t s_t st的值被更新,而unvisited states s ≠ s t s\ne s_t s=st的values保持不变。
- 在等式(2)中的更新过程在后面的内容中将被省略
对TD算法进行一些标注:
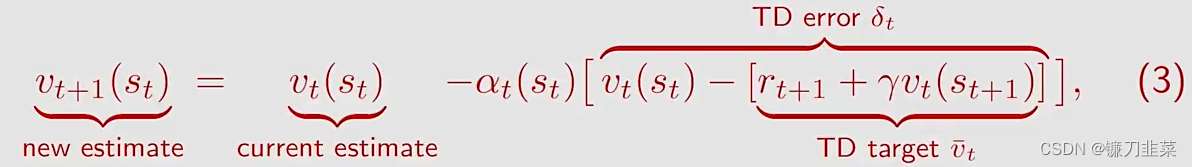
其中
v
ˉ
t
≐
r
t
+
1
+
γ
v
(
s
t
+
1
)
\bar{v}_t\doteq r_{t+1}+\gamma v(s_{t+1})
vˉt≐rt+1+γv(st+1)被称为TD target。
δ
t
≐
v
(
s
t
)
−
[
r
t
+
1
+
γ
v
(
s
t
+
1
)
]
=
v
(
s
t
)
−
v
ˉ
t
\delta_t\doteq v(s_t)-[r_{t+1}+\gamma v(s_{t+1})]=v(s_t)-\bar{v}_t
δt≐v(st)−[rt+1+γv(st+1)]=v(st)−vˉt被称为TD error。
根据上面式子,可以得出一个结论,新的估计
v
t
+
1
(
s
t
)
v_{t+1}(s_t)
vt+1(st)是整合了当前估计
v
t
(
s
t
)
v_t(s_t)
vt(st)和TD error。
首先,为什么
v
ˉ
t
\bar{v}_t
vˉt被称为TD target?This is because the algorithm drives
v
(
s
t
)
v(s_t)
v(st) towards
v
ˉ
t
\bar{v}_t
vˉt.解释如下:
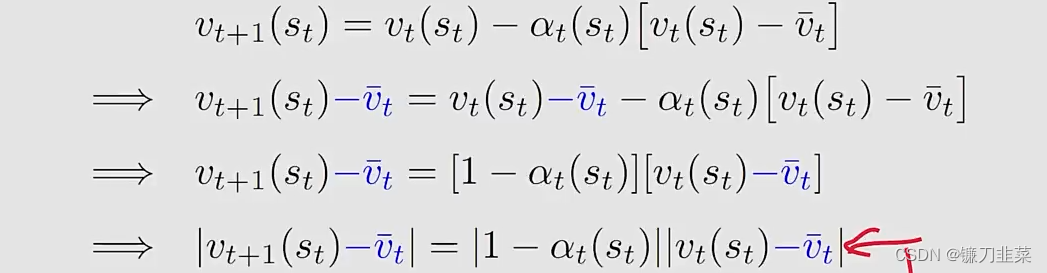
因为
α
t
(
s
t
)
\alpha_t(s_t)
αt(st)是一个较小的正数,因此有
0
<
1
−
α
t
(
s
t
)
<
1
0<1-\alpha_t(s_t)<1
0<1−αt(st)<1,因此
∣
v
t
+
1
(
s
t
)
−
v
ˉ
t
∣
≤
∣
v
t
(
s
t
)
−
v
ˉ
t
∣
|v_{t+1}(s_t)-\bar{v}_t|\le |v_t(s_t)-\bar{v}_t|
∣vt+1(st)−vˉt∣≤∣vt(st)−vˉt∣这意味着means
v
(
s
t
)
v(s_t)
v(st)是朝向
v
ˉ
t
\bar{v}_t
vˉt靠近的。
然后,怎么解释TD error呢? δ t = v ( s t ) − [ r t + 1 + γ v ( s t + 1 ) ] \delta_t= v(s_t)-[r_{t+1}+\gamma v(s_{t+1})] δt=v(st)−[rt+1+γv(st+1)]
- difference在于它们是在两个连续的时间步,一个是t时刻,另一个是t+1时刻
- 它反映了
v
t
v_t
vt和
v
π
v_\pi
vπ之间的deficiency(不一致)。为了说明这一点,将上式写为
δ
π
,
t
=
v
π
(
s
t
)
−
[
r
t
+
1
+
γ
v
π
(
s
t
+
1
)
]
\delta_{\pi, t}= v_\pi(s_t)-[r_{t+1}+\gamma v_\pi(s_{t+1})]
δπ,t=vπ(st)−[rt+1+γvπ(st+1)]对其求期望
E
[
δ
π
,
t
∣
S
t
=
s
t
]
=
v
π
(
s
t
)
−
E
[
R
t
+
1
+
γ
v
π
(
S
t
+
1
)
∣
S
t
=
s
t
]
=
0
\mathbb{E}[\delta_{\pi, t}|S_t=s_t]=v_\pi(s_t)-\mathbb{E}[R_{t+1}+\gamma v_\pi (S_{t+1})|S_t=s_t]=0
E[δπ,t∣St=st]=vπ(st)−E[Rt+1+γvπ(St+1)∣St=st]=0
- 如果 v t = v π v_t=v_\pi vt=vπ,那么 δ t \delta_t δt是应该等于0(in the expectation sense)。
- 因此,如果 δ t \delta_t δt不等于0,那么 v t v_t vt不等于 v π v_\pi vπ。
- 另外,TD error也可以被解释为innovation,也就是从experience ( s t , r t + 1 , s t + 1 ) (s_t, r_{t+1}, s_{t+1}) (st,rt+1,st+1)获得的新的信息。
TD算法的其他基本性质:
- 在公式(3)中的TD算法只能在给定策略的条件下估计state value
- 不能估计action values
- 不能搜索最优策略
不管怎样,TD算法是后面算法的基础和核心思想。
问题:在数学上,TD算法做了什么?
答:它求解一个给定策略
π
\pi
π的Bellman equation,也就是说TD算法是在没有模型的情况下来求解贝尔曼公式。
首先,引入一个新的贝尔曼公式。
π
\pi
π的state value的定义如下
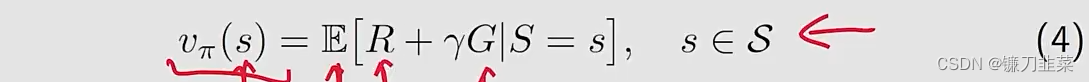
其中
G
G
G是discounted return。进一步地
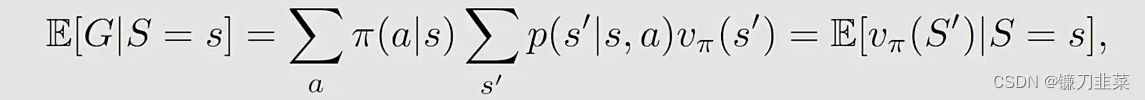
其中
S
′
S'
S′是next state,我们可以重写等式(4):
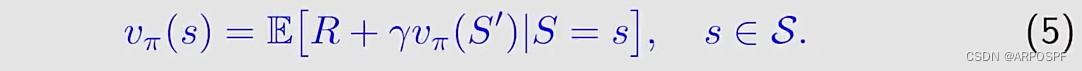
等式(5)是贝尔曼公式的另一种表达形式,也被称为Bellman expectation equation,是一个用来设计和分析TD算法的重要工具。
第二,使用RM算法求解等式(5)中的贝尔曼方程。
具体的,首先定义
g
(
v
(
s
)
)
=
v
(
s
)
−
E
[
R
+
γ
v
π
(
S
′
)
∣
s
]
g(v(s))=v(s)-\mathbb{E}[R+\gamma v_\pi(S')|s]
g(v(s))=v(s)−E[R+γvπ(S′)∣s]将等式(5)重写为
g
(
v
(
s
)
)
=
0
g(v(s))=0
g(v(s))=0因为我们仅仅可以从
R
R
R和
S
′
S'
S′中得到样本
r
r
r和
s
′
s'
s′,那么the noisy observation是:
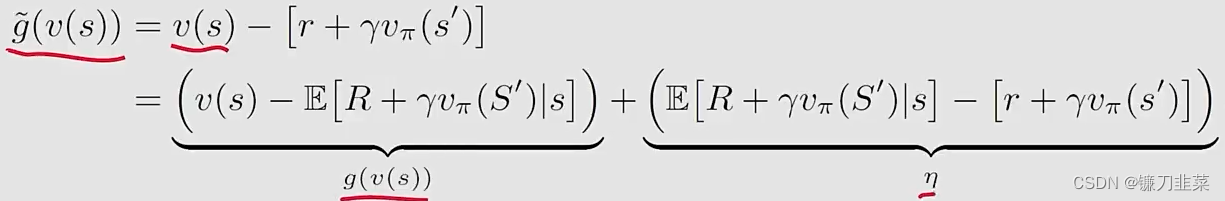
因此,求解
g
(
v
(
s
)
)
=
0
g(v(s))=0
g(v(s))=0的RM算法是:
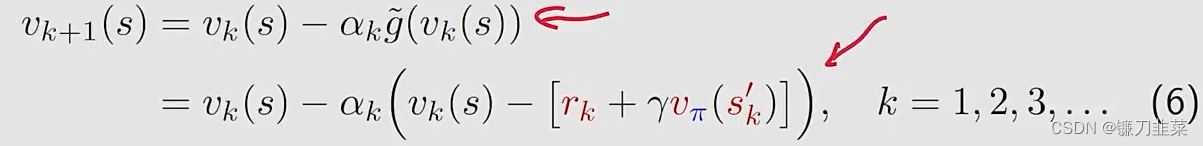
其中
v
k
(
s
)
v_k(s)
vk(s)是在k步的
v
π
(
s
)
v_\pi(s)
vπ(s)的估计,
r
k
,
s
k
′
r_k, s'_k
rk,sk′是在k步的
R
,
S
′
R,S'
R,S′的采样。但是这里有两个小的不同点:
等式(6)中的RM算法具有两个假设值得特别关注:
- We must have the experience set { ( s , r , s ′ ) } \{(s,r,s')\} {(s,r,s′)} for k = 1 , 2 , 3 , . . . k=1,2,3,... k=1,2,3,...
- We assume that KaTeX parse error: Expected group as argument to '\v' at position 3: \v_̲pi (s') is already known for any s ′ s' s′。
为了消除RM算法中的这两个假设,我们的修改点是:
- 将 { ( s , r , s ′ ) } \{(s,r,s')\} {(s,r,s′)}变为 { ( s t , r t + 1 , s t + 1 ) } \{(s_t,r_{t+1},s_{t+1})\} {(st,rt+1,st+1)},这样算法就可以在一个episode中利用sequential samples。
- 另一个修改是用KaTeX parse error: Expected group as argument to '\v' at position 3: \v_̲pi (s')的一个估计来替代KaTeX parse error: Expected group as argument to '\v' at position 3: \v_̲pi (s'),因为我们事先并不知道KaTeX parse error: Expected group as argument to '\v' at position 3: \v_̲pi (s')
算法收敛性

需要注意的是:
- 该定理说明对于一个给定的policy π \pi π, state value可以由TD算法找到
- ∑ t α t ( s ) = ∞ \sum_t \alpha_t(s)=\infty ∑tαt(s)=∞和 ∑ t α t 2 ( s ) < ∞ \sum_t \alpha_t^2(s)<\infty ∑tαt2(s)<∞对于所有 s ∈ S s\in S s∈S必须是成立的。在时间步 t t t,如果 s = s t s=s_t s=st,这意味着在时刻t, s s s是visited,然后 α t ( s ) > 0 \alpha_t(s)>0 αt(s)>0;否则, α t ( s ) = 0 \alpha_t(s)=0 αt(s)=0对于所有的其他 s ≠ s t s\ne s_t s=st。即要求每个state必须被访问了很多次(sufficiently many)
- 通常learning rate α \alpha α被设置为一个较小的常数,比如0.00几。在这种情况下,条件 ∑ t α t 2 ( s ) < ∞ \sum_t \alpha_t^2(s)<\infty ∑tαt2(s)<∞不再满足,但是实际当中为什么这么做呢,就是因为当 α \alpha α是一个常数时,算法很久之后所得到的这些经验仍然能够派上用场,相反如果 α t \alpha_t αt最后是趋向于0,那很久之后这些经验就没用了,所以将其设置为一个很小的数,但是不让它完全收敛到0。(when α is constant, it can still be shown that the algorithm converges in the sense of expectation sense.)
Algorithm properties:
尽管TD learning和MC learning都是model-free方法,与MC learning相比,TD learning的优点和缺点分别是什么呢?
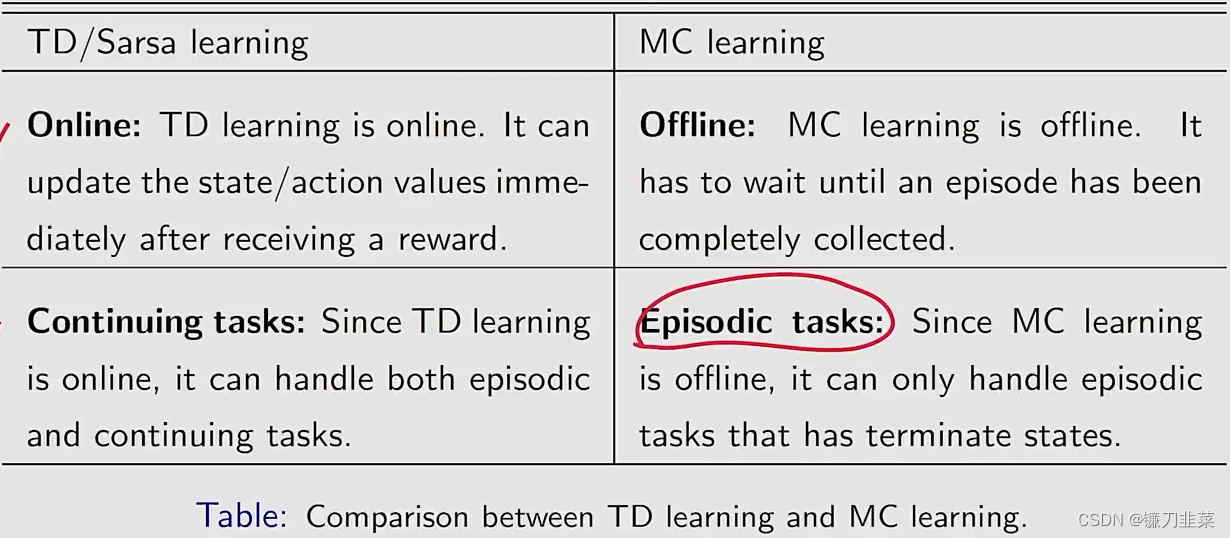
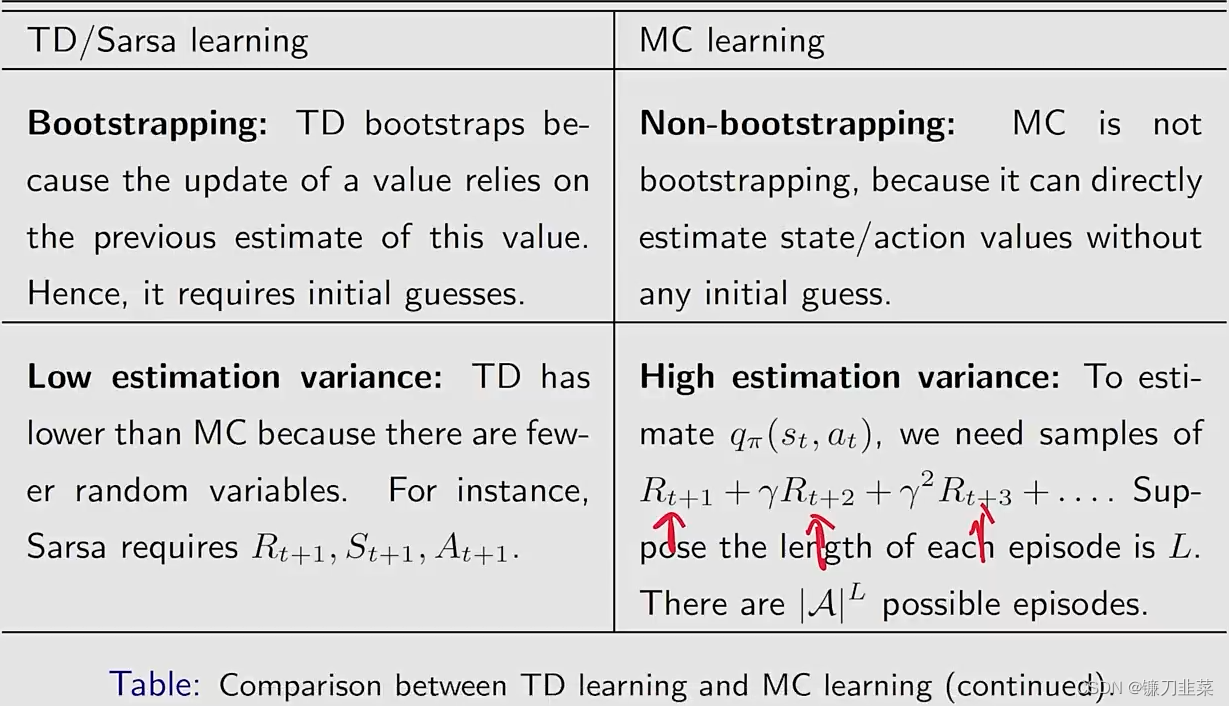
另外一个方面就是随机变量实际上有两个性质,第一个是variance,第二个是它的expectation或者是mean。虽然这个TD算法它的variance是比较小的,但是它的mean或者expectation是有bias的。为什么呢?因为它是bootstrapping,它依赖于初始的估计,如果初始的估计不太准确的话,那么这个不准确的估计会进入到这个估计的过程中造成bias。当然随着越来越多的数据进来,会逐渐把bias给抵消掉,直到最后能够收敛到一个正确的估计值。相反MClearning,虽然有比较高的variance,但是因为它不涉及任何的初始值,它的expectation实际上就直接等于它真实的action value或者是state value,所以它是无偏估计。
TD learning of action values: Sarsa
上一节中介绍的TD算法仅仅可以用来估计state values。这一小节的Sarsa算法可以用来直接估计action values,同时也将会介绍如何使用Sarsa算法找到最后的policies.
Algorithm:
首先,我们的目标是基于一个给定的策略
π
\pi
π估计action values。没有模型的时候我们要有数据或者要有experience,所以假设我们有experience
{
(
s
t
,
a
t
,
r
t
+
1
,
s
t
+
1
,
a
t
+
1
)
}
t
\{(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1})\}_t
{(st,at,rt+1,st+1,at+1)}t。我们可以使用下面的Sarsa算法去估计action values:
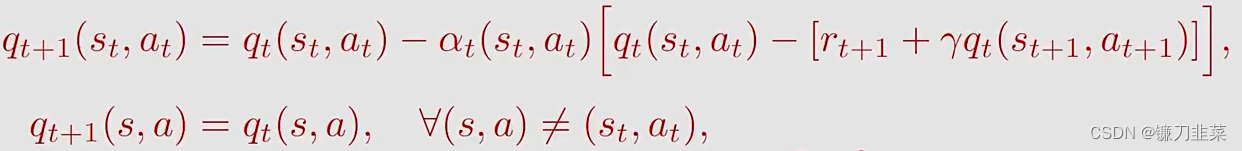
其中
t
=
0
,
1
,
2
,
.
.
.
.
.
.
t=0,1,2,......
t=0,1,2,......
- q t ( s t , a t ) q_t(s_t, a_t) qt(st,at)是 q π ( s t , a t ) q_\pi (s_t, a_t) qπ(st,at)的估计;
- α t ( s t , a t ) \alpha_t(s_t, a_t) αt(st,at)是依赖于 s t , a t s_t, a_t st,at的learning rate。
为什么称为Sarsa算法呢?因为在算法的每一步涉及
(
s
t
,
a
t
,
r
t
+
1
,
s
t
+
1
,
a
t
+
1
)
(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1})
(st,at,rt+1,st+1,at+1)。Sarsa is the abbreviation of state-action-reward-state-action。
Sarsa和上一节中的TD learning算法的关系是什么?我们通过将TD算法中的state value estimate
v
(
s
)
v(s)
v(s)替换为action value estimate
q
(
s
,
a
)
q(s, a)
q(s,a)就得到了Sarsa。因此,Sarsa is an action-value version of the TD algorithm。
Sarsa算法解决一个什么样的数学问题呢?Sarsa的表达式表明它是一个求解如下方程的stochastic approximate algorithm:
q
π
(
s
,
a
)
=
E
[
R
+
γ
q
π
(
S
′
,
A
′
)
∣
s
,
a
]
,
∀
s
,
a
q_\pi(s, a)=\mathbb{E}[R+\gamma q_\pi(S', A')|s, a], \forall s,a
qπ(s,a)=E[R+γqπ(S′,A′)∣s,a],∀s,a这是贝尔曼方程针对action value的另一种表达形式。
Sarsa算法的收敛性

这个定理告诉我们对于一个给定的策略
π
\pi
π,可以通过Sarsa找到action value。
为了得到最优的policy,还需要把这个过程和一个policy improvement相结合才可以。
Implementation
RL的最终目标是找到最优策略。为了达到这个目的,我们将Sarsa和一个policy improvement step相结合,这个结合的算法也称为Sarsa。

需要注意的是:
- 当 q ( s t , a t ) q(s_t, a_t) q(st,at)更新之后, s t s_t st的policy将会立即更新。这是基于generalized policy iteration的思想。
- 策略更新是 ϵ \epsilon ϵ-greedy,而不是greedy,它能较好地平衡exploitation和exploration.
需要强调的是:
- 核心思想是简单的:即使用算法求解给定策略下的贝尔曼公式;
- The complication emerges when we try to find optimal policies and work efficiently。
举个例子:任务的目标是找到一条较好的路径,从一个特定的starting state到target state。任务设定 r t a r g e t = 0 , r f o r b i d d e n = r b o u n d a r y = − 10 , r o t h e r = − 1 r_{target}=0, r_{forbidden}=r_{boundary}=-10, r_{other}=-1 rtarget=0,rforbidden=rboundary=−10,rother=−1,学习率 α = 0.1 \alpha=0.1 α=0.1, ϵ \epsilon ϵ的值是0.1。
- 这个任务和之前的任务不同,之前的任务是需要对每个state找到最优的策略
- 每个episode从top-left state开始,在target state终止
- In the future, pay attention to what the task is.
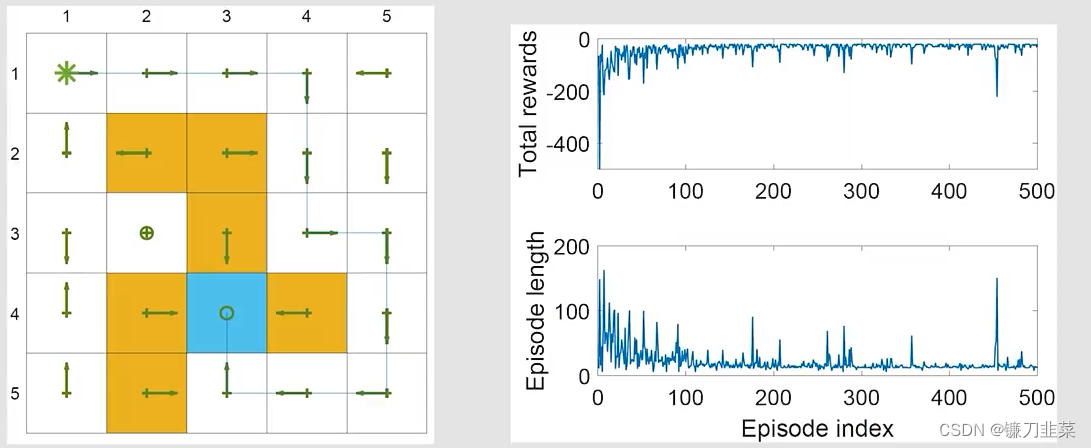
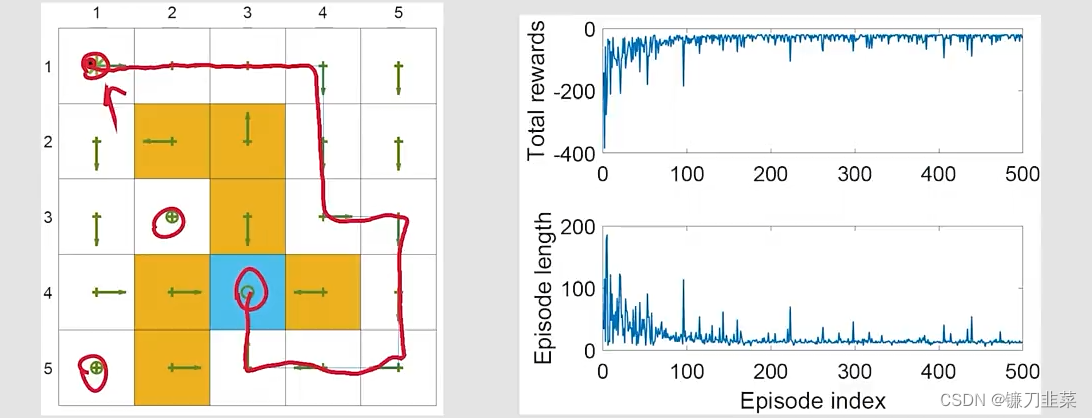
结果:
- 左边的图表示Sarsa找到的最终策略。可以看到并不是所有的state拥有最优策略。
- 右边的图表示总的reward和每个episode的长度。the metric of total reward per episode will be frequently used。
TD learning of action values: Expected Sarsa
Expected Sarsa算法是Sarsa的一个变体:
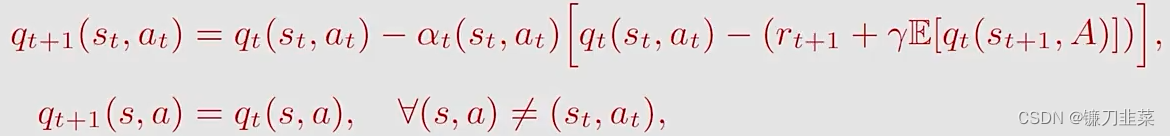
其中
E
[
q
t
(
s
t
+
1
,
A
)
]
=
∑
a
π
t
(
a
∣
s
t
+
1
)
q
t
(
s
t
+
1
,
a
)
≐
v
t
(
s
t
+
1
)
\mathbb{E}[q_t(s_{t+1}, A)]=\sum _a \pi_t(a|s_{t+1})q_t(s_{t+1}, a)\doteq v_t(s_{t+1})
E[qt(st+1,A)]=a∑πt(a∣st+1)qt(st+1,a)≐vt(st+1)是策略
π
t
\pi_t
πt下的
q
t
(
s
t
+
1
,
A
)
q_t(s_{t+1}, A)
qt(st+1,A)的expected value。
与Sarsa相比,它的区别是:
- TD target从Sarsa中的 r t + 1 + γ q t ( s t + 1 , a t + 1 ) r_{t+1}+\gamma q_t(s_{t+1}, a_{t+1}) rt+1+γqt(st+1,at+1)变为Expected Sarsa中的 r t + 1 + γ E [ q t ( s t + 1 , A ) ] r_{t+1}+\gamma \mathbb{E}[q_t(s_{t+1}, A)] rt+1+γE[qt(st+1,A)]。
- 需要更多的计算,但是因为随机变量从 ( s t , a t , r t + 1 , s t + 1 , a t + 1 ) (s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1}) (st,at,rt+1,st+1,at+1)变为 ( s t , a t , r t + 1 , s t + 1 ) (s_t, a_t, r_{t+1}, s_{t+1}) (st,at,rt+1,st+1),减少了随机变量,所以减少了estimation variances。
**Expected Sarsa在解决一个什么样的数学问题呢?**同样的,Expected Sarsa也是在求解一个贝尔曼公式,只不过这个贝尔曼公式的形式发生了一些变化。具体来说,Expected Sarsa是求解下面等式的一个stochastic approximate algorithm:
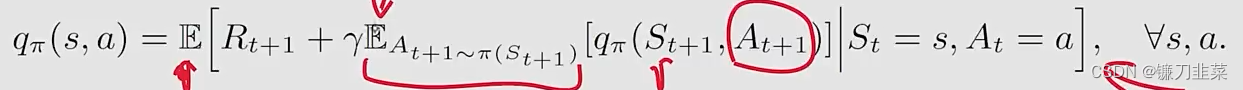
上面等式是贝尔曼公式的另一个表达形式:
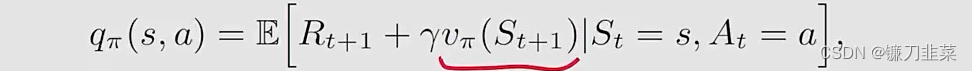
举个例子:
TD learning of action values: n-step Sarsa
n-Step Sarsa是Sarsa的一个变型或者是一个推广,因为n-step Sarsa包含了Sarsa和蒙特卡洛两种方法,也就是can unify Sarsa and Monte Carlo learning。
action value的定义如下:
q
π
(
s
,
a
)
=
E
[
G
t
∣
S
t
=
s
,
A
t
=
a
]
q_\pi(s,a)=\mathbb{E}[G_t|S_t=s, A_t=a]
qπ(s,a)=E[Gt∣St=s,At=a]
discounted return
G
t
G_t
Gt可以写为另一种形式
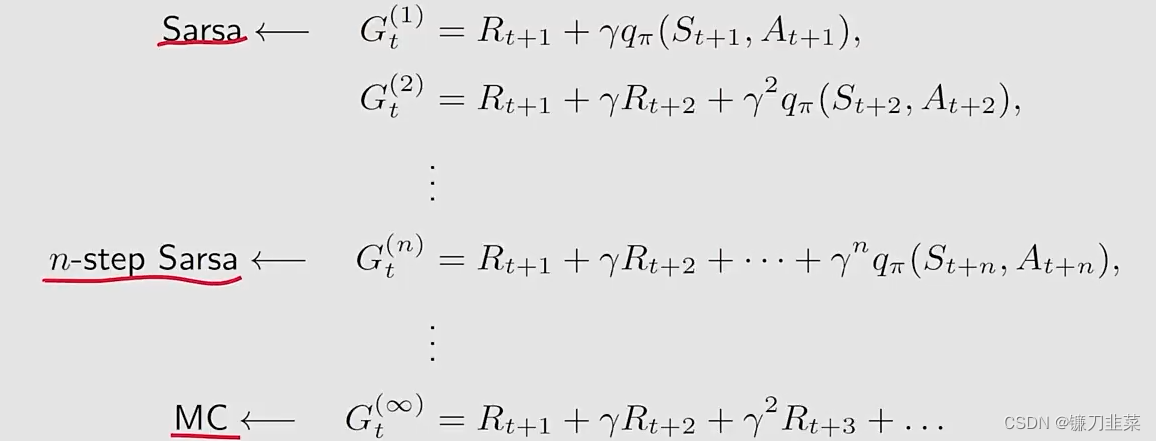
注意这里边所有含有上标的这些
G
t
G_t
Gt都是等价的。只不过它们之间的不同是基于它们怎么样去分解。
使用
G
t
(
1
)
G_t^{(1)}
Gt(1)带入action value,得到Sarsa的action value公式:
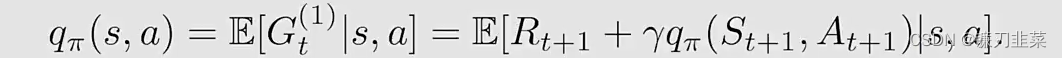
使用
G
t
(
∞
)
G_t^{(\infty)}
Gt(∞)带入action value,得到MC learning的action value求解公式:
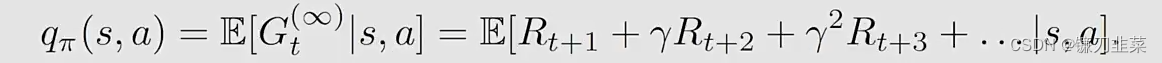
因此,一个中间的算法称为n-step Sarsa,其action value求解公式为:
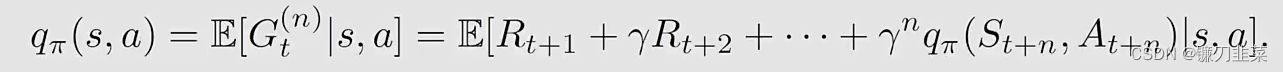
因此n-step Sarsa算法是:
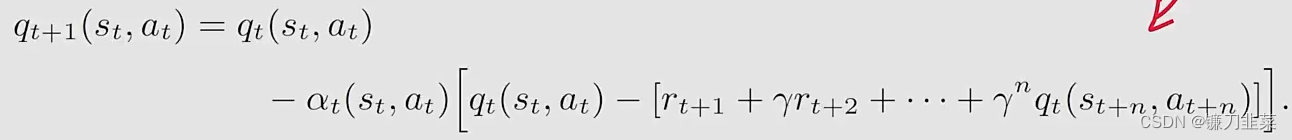
当n=1的时候,n-step Sarsa就变成了(one-step)Sarsa算法,如果
n
=
∞
n=\infty
n=∞,n-step Sarsa变成了MC learning算法。
对Sarsa的一些性质分析:
- n-step Sarsa需要 ( s t , a t , r t + 1 , s t + 1 , a t + 1 , . . . , r t + n , s t + n , a t + n ) (s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1},..., r_{t+n}, s_{t+n}, a_{t+n}) (st,at,rt+1,st+1,at+1,...,rt+n,st+n,at+n)
- 因为在时刻t,不知道
(
r
t
+
n
,
s
t
+
n
,
a
t
+
n
)
(r_{t+n}, s_{t+n}, a_{t+n})
(rt+n,st+n,at+n),所以在t步,不能实现n-step Sarsa。我们必须等待t+n时刻才能更新
(
s
t
,
a
t
)
(s_t, a_t)
(st,at)的q-value:
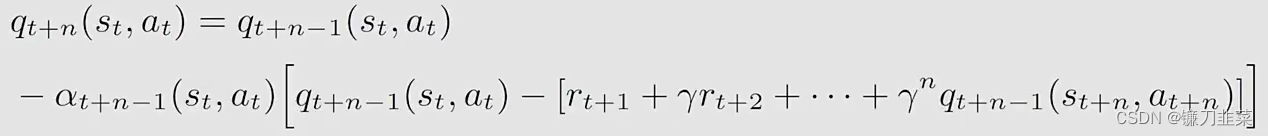
- 因为MC learning和Sarsa实际上是n-step Sarsa的两个极端情况,因此,它的性质是Sarsa和MC learning性质的混合:
- 如果n较大,它的性质接近MC learning,因此具有一个较大的variance,但是有一个较小的bias;
- 如果n较小,它的性质接近Sarsa,因此由于initial guess具有一个相对大的bias,但是具有相对较低的variance。
- 最终, n-step Sarsa实际上还是在做policy evaluation,因此它需要和policy improvement step结合以寻找最优策略。
TD learning of optimal action values: Q-learning
Sarsa基于一个给定的policy估计action value,它必须整合policy improvement step才能寻找最优策略。而Q-learning直接估计optimal action values,不需要去做policy evaluation和policy improvement,在这两个之间来回交替运行。
Q-learning Algorithm:
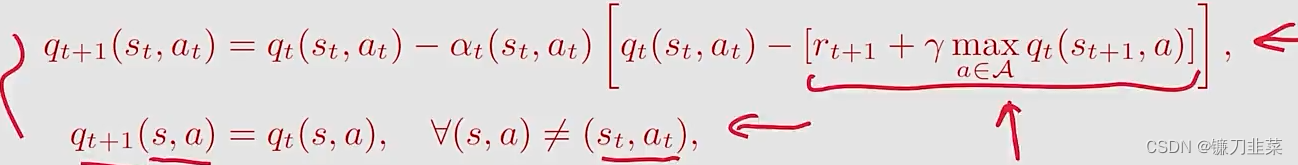
从形式上看,Q-learning与Sarsa非常相似,唯一的不同在于TD target:
- Q-learning的TD target是 r t + 1 + γ max a ∈ A q t ( s t + 1 , a ) r_{t+1}+\gamma \max_{a\in A}q_t(s_{t+1, a}) rt+1+γmaxa∈Aqt(st+1,a)
- Sarsa的TD target是 r t + 1 + γ q t ( s t + 1 , a t + 1 ) r_{t+1}+\gamma q_t(s_{t+1}, a_{t+1}) rt+1+γqt(st+1,at+1)
**Q-learning在数学上解决什么问题呢?它旨在解决 q ( s , a ) = E [ R t + 1 + γ max a q ( S t + 1 , a ) ∣ S t = s , A t = a ] , ∀ s , a q(s,a)=\mathbb{E}[R_{t+1}+\gamma \max_a q(S_{t+1}, a)|S_t=s, A_t=a], \forall s,a q(s,a)=E[Rt+1+γamaxq(St+1,a)∣St=s,At=a],∀s,a这是贝尔曼最优公式(Bellman optimality equation)**针对action value的表达式。
Off-policy vs On-policy:
首先,在TD learning task中存在两个策略:
- 第一个是
behavior policy,是和环境进行交互然后生成experience samples - 第二个是
target policy,一直更新它,直到最后得到一个最优策略
基于behavior policy和target policy,定义两种策略类型:On-policy和Off-policy:
- 当behavior policy和target policy相同的时候,这样的学习策略称为on-policy
- 当它们不同的时候,the learning称为off-policy
off-policy learning的好处是:
- 可以从之前别人的经验当中学习:It can search for optimal policies based on the experience samples generated by any other policies.
- 作为一个重要的特殊情况, the behavior policy can be selected to be exploratory(探索性)。例如,如果我们想要对于所有state-action pairs估计action values,我们可以使用一个探索性的策略生成episodes,去visiting每个state-action pair许多次。
如何判断一个TD算法是on-policy还是off-policy?
- 首先,检查这个算法在数学上解决什么问题,
- 然后,检查这个算法在实施过程中需要哪些东西才能让算法跑起来。
It deserves special attention because it is one of the most confusing problems.
Sarsa是on-policy。
- 首先,Sarsa aims to solve the Bellman equation of a given policy π \pi π: q π ( s , a ) = E [ R + γ q π ( S ′ , A ′ ) ∣ s , a ] , ∀ s , a q_\pi(s,a)=\mathbb{E}[R+\gamma q_\pi (S', A')|s,a], \forall s,a qπ(s,a)=E[R+γqπ(S′,A′)∣s,a],∀s,a其中 R ∼ p ( R ∣ s , a ) R\sim p(R|s, a) R∼p(R∣s,a), S ′ ∼ p ( S ′ ∣ s , a ) S'\sim p(S'|s,a) S′∼p(S′∣s,a), A ′ ∼ π ( A ′ ∣ S ′ ) A'\sim \pi(A'|S') A′∼π(A′∣S′)
- 第二,算法如下
q
t
+
1
(
s
t
,
a
t
)
=
q
t
(
s
t
,
a
t
)
−
α
t
(
s
t
,
a
t
)
[
q
t
(
s
t
,
a
t
)
−
[
r
t
+
1
+
γ
q
t
(
s
t
+
1
,
a
t
+
1
)
]
]
q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha _t(s_t,a_t)[q_t(s_t,a_t)-[r_{t+1}+\gamma q_t(s_{t+1},a_{t+1})]]
qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γqt(st+1,at+1)]]其中需要
(
s
t
,
a
t
,
r
t
+
1
,
s
t
+
1
,
a
t
+
1
)
(s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1})
(st,at,rt+1,st+1,at+1)
- 如果 ( s t , a t ) (s_t, a_t) (st,at)给定,那么 r t + 1 r_{t+1} rt+1和 s t + 1 s_{t+1} st+1不依赖于任何策略!
- a t + 1 a_{t+1} at+1 is generated following π t ( s t + 1 ) \pi_t(s_{t+1}) πt(st+1)!
- π t \pi_t πt既是一个target policy,又是一个behavior policy。
Monte Carlo learning是on-policy。
- 首先,MC方法要解决的问题是 q π ( s , a ) = E [ R t + 1 + γ R t + 1 + . . . ∣ S t = s , A t = a ] , ∀ s , a q_\pi(s,a)=\mathbb{E}[R_{t+1}+\gamma R_{t+1}+...|S_t=s, A_t=a], \forall s,a qπ(s,a)=E[Rt+1+γRt+1+...∣St=s,At=a],∀s,a其中the sample is generated following a given policy π \pi π。
- 第二,MC方法的实现是 q ( s , a ) ≈ r t + 1 + γ r t + 2 + . . . q(s,a)\approx r_{t+1}+\gamma r_{t+2}+... q(s,a)≈rt+1+γrt+2+...
- A policy被用于生成采样,也进一步被用于估计策略的action values。基于这个action values,我们可以改进policy。
Q-learning is off-policy。
- 首先,看Q-learning在数学上解决的问题,它用于求解贝尔曼最优方程: q ( s , a ) = E [ R t + 1 + γ max a q ( S t + 1 , a ) ∣ S t = s , A t = a ] , ∀ s , a q(s,a)=\mathbb{E}[R_{t+1}+\gamma \max_a q(S_{t+1},a)|S_t=s, A_t=a], \forall s,a q(s,a)=E[Rt+1+γamaxq(St+1,a)∣St=s,At=a],∀s,a
- 第二,看实施Q-learning需要什么样的测量。算法如下:
q
t
+
1
(
s
t
,
a
t
)
=
q
t
(
s
t
,
a
t
)
−
α
t
(
s
t
,
a
t
)
[
q
t
(
s
t
,
a
t
)
−
[
r
t
+
1
+
γ
max
a
∈
A
q
t
(
s
t
+
1
,
a
)
]
]
q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha _t(s_t,a_t)[q_t(s_t,a_t)-[r_{t+1}+\gamma \max_{a\in \mathcal{A}}q_t(s_{t+1}, a)]]
qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γa∈Amaxqt(st+1,a)]]需要
(
s
t
,
a
t
,
r
t
+
1
,
s
t
+
1
)
(s_t, a_t, r_{t+1}, s_{t+1})
(st,at,rt+1,st+1)
- 如果 ( s t , a t ) (s_t, a_t) (st,at)给定,那么 r t + 1 r_{t+1} rt+1和 s t + 1 s_{t+1} st+1不依赖于任何策略!
- 所以Q-learning中的behavior policy是需要从 s t s_t st出发根据一个策略得到一个 a t a_t at,target policy是最优策略。因此Q-learning中的behavior policy和target policy是不同的,也就是说Q-learning是off-policy。
因为Q-learning的behavior policy和target policy是不同的,也就是说它也可以on-policy,相同是不同的特殊形式,它可以用off-policy或者on-policy的方式来实现。
Policy searching by Q-learning (On-policy version):

Policy searching by Q-learning (Off-policy version):

举个例子:在网格世界中,找到所有states的一个最优策略。任务设定
r
t
a
r
g
e
t
=
1
,
r
f
o
r
b
i
d
d
e
n
=
r
b
o
u
n
d
a
r
y
=
−
1
r_{target}=1, r_{forbidden}=r_{boundary}=-1
rtarget=1,rforbidden=rboundary=−1,学习率
α
=
0.1
\alpha=0.1
α=0.1,discount rate
γ
\gamma
γ的值是0.9。
Ground truth: an optimal policy and the corresponding optimal state values.
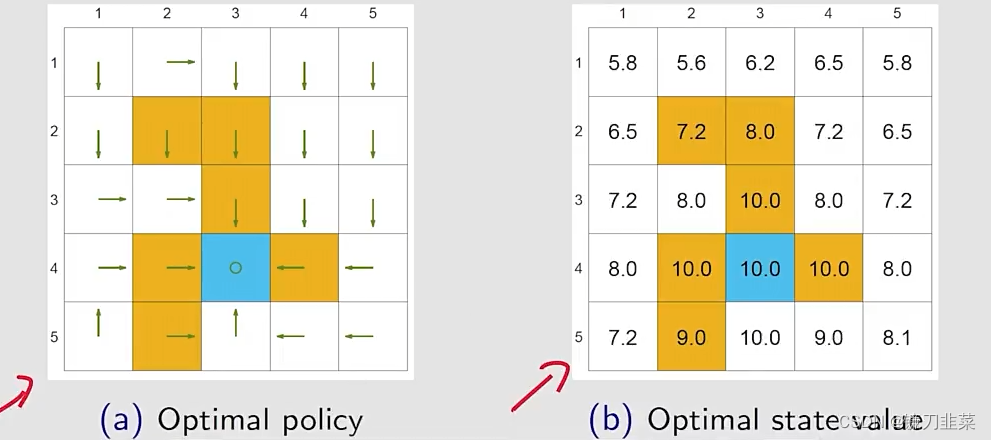
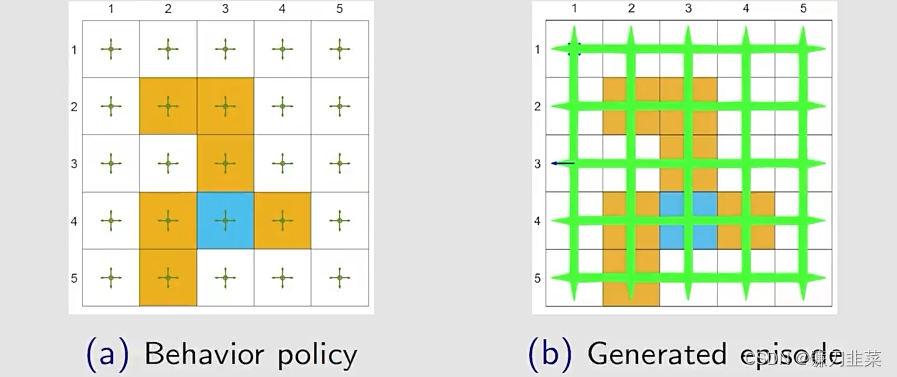
首先,选定一个behavior policy,然后用这个behavior policy产生很多的data/experience(1 million steps):
由off-policy Q-learning找到的policy:
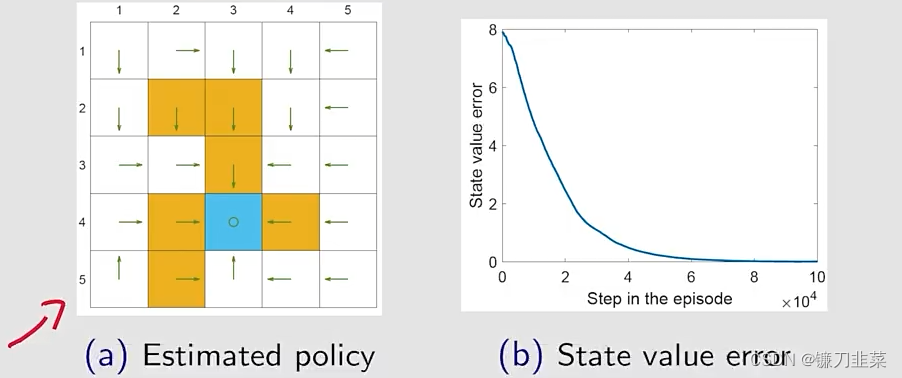
上面的策略是探索性比较强的,因为要在每一个state找出最优的策略。The importance of exploration: episodes of 1 million steps.
如果策略的探索性不是那么强,the samples are not good.
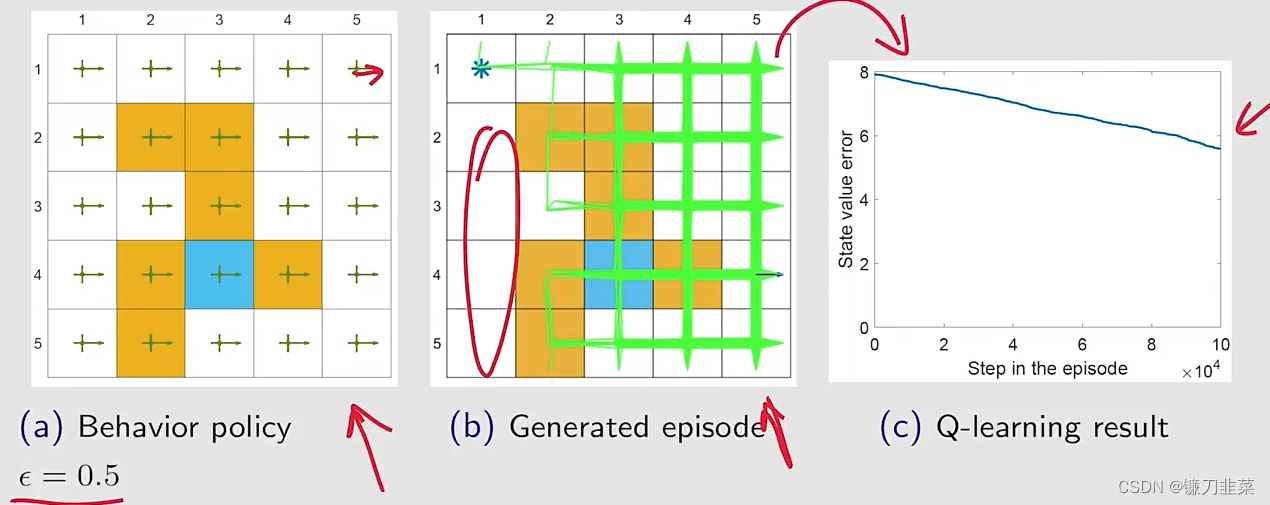
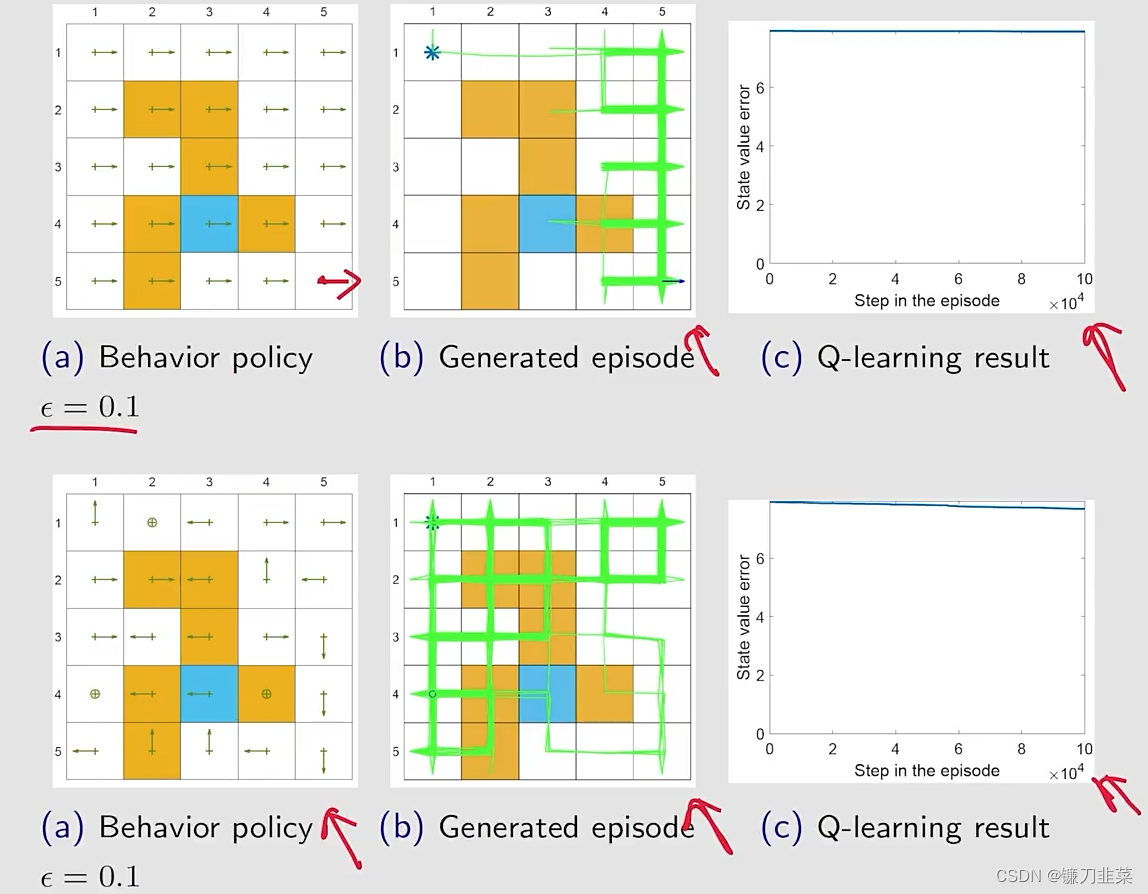
如果探索性更弱一些,比如
ϵ
=
0.1
\epsilon=0.1
ϵ=0.1:
A unified point of view
上面所介绍的所有算法都可以用一个统一的表达式表示出来:
q
t
+
1
(
s
t
,
a
t
)
=
q
t
(
s
t
,
a
t
)
−
α
t
(
s
t
,
a
t
)
[
q
t
(
s
t
,
a
t
)
−
q
ˉ
t
]
q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha _t(s_t,a_t)[q_t(s_t,a_t)-\bar{q}_t]
qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−qˉt],其中
q
ˉ
t
\bar{q}_t
qˉt是TD target。
所有的TD算法之间的不同点在于
q
ˉ
t
\bar{q}_t
qˉt:

MC方法也可以用这个统一的表达式表示,通过设定
α
t
(
s
t
,
a
t
)
=
1
\alpha_t(s_t, a_t)=1
αt(st,at)=1,有
q
t
+
1
(
s
t
,
a
t
)
=
q
ˉ
t
q_{t+1}(s_t, a_t)=\bar{q}_t
qt+1(st,at)=qˉt
除了统一的形式之外,它们做的事情也可以统一地写出来。上面的所有算法可以被视为求解贝尔曼方程或者贝尔曼最优方程的stochastic approximate algorithms:

这些TD方法从本质上说是来求解一个给定策略的贝尔曼公式,但是怎么让它来搜索最优的策略呢?其实就是把policy evaluation这个步骤和policy improvement相结合,就得到一个搜索最优策略的算法。
Summary
时序差分算法的核心思想是用对未来动作选择的价值估计来更新对当前动作选择的价值估计,这是强化学习中的核心思想之一。
内容来源
- 《强化学习的数学原理》 西湖大学工学院赵世钰教授 主讲
- 《动手学强化学习》 俞勇 著