一、简介

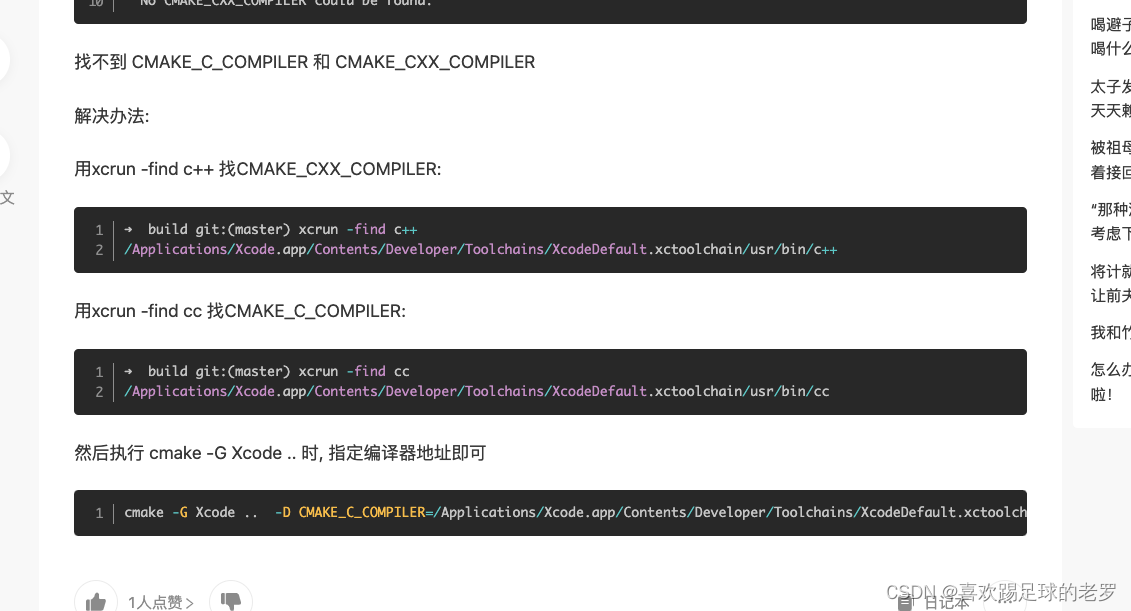
爱因斯坦求和约定(Einstein summation convention)是一种标记的约定, 又称为爱因斯坦标记法(Einstein notation), 可以基于一些约定简写格式表示多维线性代数数组操作，让表达式更加简洁明了。

既然是约定，那我们就来看看都约定了什么，主要有如下两点：

1.哑标

公式中不同字母分别有重复一次的上角标和下角标时，视为求和。下图中的i和j都是哑标。

$\sum_{i=1}^{3}a_{i}b_{i}=a_{i}b_{i}$

$\sum_{i=1}^{3}\sum_{j=1}^{3}a_{ij}x_{i}y_{j}=a_{ij}x_{i}y_{j}$

2.自由标

在公式的每一项中，仅出现一次的下角标，代表一个维度，下图中i是自由标、j是哑标。

$y_{1}=a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}$

$y_{2}=a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}$

$y_{3}=a_{31}x_{1}+a_{32}x_{2}+a_{33}x_{3}$

爱因斯坦和表示为

$y_{i}=a_{ij}x_{j}$

二、torch实现

Einsum在torch、tf和numpy中都有实现，而且用方式差不多，这里我们以torch为例。

总体思想是用一些下标标记输入的每个维度，并定义哪些下标是输出的一部分。然后，通过将操作中下标不属于输出的维度的元素的乘积求和来计算输出。下面是一些例子，还是很好理解的。

1.计算迹

没有显式的输出就是求和在输出。

torch.einsum('ii', torch.randn(4, 4))
# tensor(-1.2104)

2.取矩阵对角线

torch.einsum('ii->i', torch.randn(4, 4))
# tensor([-0.1034,  0.7952, -0.2433,  0.4545])

3.计算外积

x = torch.randn(5)
y = torch.randn(4)
torch.einsum('i,j->ij', x, y)
# tensor([[ 0.1156, -0.2897, -0.3918,  0.4963],
#         [-0.3744,  0.9381,  1.2685, -1.6070],
#         [ 0.7208, -1.8058, -2.4419,  3.0936],
#         [ 0.1713, -0.4291, -0.5802,  0.7350],
#         [ 0.5704, -1.4290, -1.9323,  2.4480]])

4.batch矩阵乘法

一行代码，将转置和乘法放在一起，确实很方便。

As = torch.randn(3,2,5)
Bs = torch.randn(3,5,4)
torch.einsum('bij,bjk->bik', As, Bs)
# tensor([[[-1.0564, -1.5904,  3.2023,  3.1271],
#          [-1.6706, -0.8097, -0.8025, -2.1183]],
# 
#         [[ 4.2239,  0.3107, -0.5756, -0.2354],
#          [-1.4558, -0.3460,  1.5087, -0.8530]],
# 
#         [[ 2.8153,  1.8787, -4.3839, -1.2112],
#          [ 0.3728, -2.1131,  0.0921,  0.8305]]])

5.带有子列表和省略号

As = torch.randn(3,2,5)
Bs = torch.randn(3,5,4)
torch.einsum(As, [..., 0, 1], Bs, [..., 1, 2], [..., 0, 2])
# tensor([[[-1.0564, -1.5904,  3.2023,  3.1271],
#          [-1.6706, -0.8097, -0.8025, -2.1183]],
# 
#         [[ 4.2239,  0.3107, -0.5756, -0.2354],
#          [-1.4558, -0.3460,  1.5087, -0.8530]],
# 
#         [[ 2.8153,  1.8787, -4.3839, -1.2112],
#          [ 0.3728, -2.1131,  0.0921,  0.8305]]])

6.变换维度

A = torch.randn(2, 3, 4, 5)
torch.einsum('...ij->...ji', A).shape
# torch.Size([2, 3, 5, 4])

7.双线性变换，类似于torch.nn.functional.bilinear

l = torch.randn(2,5)
A = torch.randn(3,5,4)
r = torch.randn(2,4)
torch.einsum('bn,anm,bm->ba', l, A, r)
# tensor([[-0.3430, -5.2405,  0.4494],
#         [ 0.3311,  5.5201, -3.0356]])

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/397792.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！