开源代码:D2-Net
1 摘要
在这项工作中,我们解决了在困难的成像条件下寻找可靠的像素级对应的问题。我们提出了一种由单一卷积神经网络发挥双重作用的方法:它同时是一个密集的特征描述符和一个特征检测器。通过将检测推迟到后期阶段,所获得的关键点比基于低层结构早期检测的传统关键点更稳定。我们证明了该模型可以使用从现成的大规模SfM重建中提取的像素对应来训练,而不需要任何进一步的注释。该方法在困难的亚琛昼夜定位数据集和InLoc室内定位基准上都获得了最先进的性能,以及在其他图像匹配和三维重建基准上具有竞争力的性能。
2 理论介绍
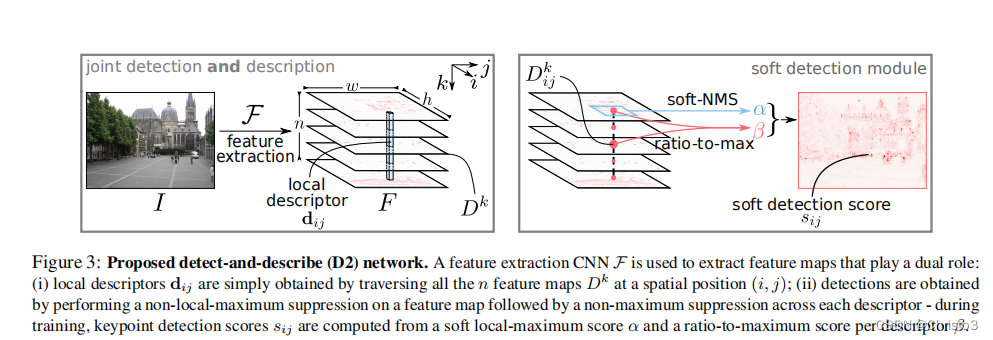
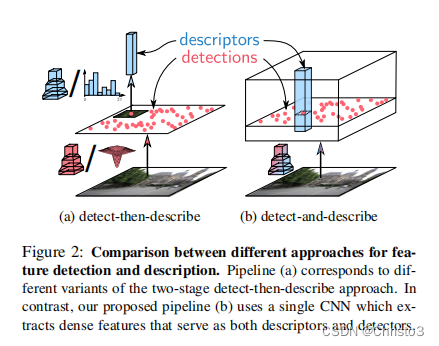
与经典的使用两阶段管道的检测然后描述方法相反,我们建议执行密集的特征提取,以获得同时是检测器和描述符的表示。因为检测器和描述符都共享底层表示,所以我们将我们的方法称为D2。我们的方法如图3所示。
该方法的第一步是对输入图像
I
I
I应用一个CNN
F
F
F,得到一个三维张量
F
=
F
(
I
)
F = F (I)
F=F(I),
F
∈
R
h
×
w
×
n
F∈R^{h×w×n}
F∈Rh×w×n,其中
h
×
w
h×w
h×w是特征图的空间分辨率,
n
n
n是通道数。
2.1. Feature Description
正如在之前的其他工作[38,44,59]中一样,对三维张量F的最直接的解释是作为一个密集的描述符向量
d
d
d的集合:
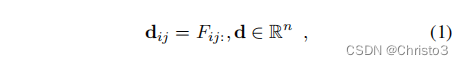
与
i
=
1
,
…
…
,
h
i = 1,……,h
i=1,……,h和
j
=
1
,
…
…
,
w
j = 1,……,w
j=1,……,w。这些描述符向量可以很容易地在图像之间进行比较,以建立对应使用欧氏距离。在训练阶段,这些描述符将被调整,使场景中相同的点产生相似的描述符,即使图像包含强烈的外观变化。在实践中,我们在比较描述符之前对描述符应用L2归一化:
d
^
i
j
=
d
i
j
/
∥
d
i
j
∥
2
.
\hat{\mathbf{d}}_{i j}=\mathbf{d}_{i j}/\|\mathbf{d}_{i j}\|_{2}.
d^ij=dij/∥dij∥2.
2.2 Feature Detection
对三维张量
F
F
F的另一种解释是作为二维响应D的集合
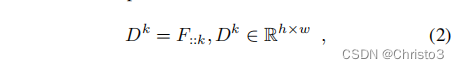
其中,
k
,
=
,
1
,
…
…
,
n
k,=,1,……,n
k,=,1,……,n。在这种解释中,特征提取函数
F
F
F可以看作是
n
n
n个不同的特征检测器函数
D
k
D^k
Dk,每个函数产生一个二维响应映射
D
k
D^k
Dk。这些检测响应图类似于在尺度不变特征变换(SIFT)[30]中获得的高斯差分(DoG)响应图或在Harris的角检测器[19]中获得的角度得分图。在我们的工作中,这些原始分数经过后处理,只选择一个位置子集作为输出关键点。下面将描述这个过程。
Hard feature detection
在传统的特征检测器如DoG中,检测图将通过执行空间非局部最大抑制来稀疏化。然而,在我们的方法中,与传统的特征探测器相反,存在多个检测映射
D
k
(
k
=
1
,
…
…
,
n
)
D^k(k = 1,……,n)
Dk(k=1,……,n),并且可以对其中的任何一个检测映射进行检测。因此,对于要检测到的一个点
(
i
、
j
)
(i、j)
(i、j),我们要求:
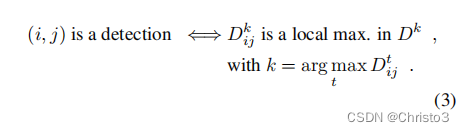
直观地说,对于每个像素
(
i
,
j
)
(i,j)
(i,j),这对应于选择最卓越的检测器
D
k
D^k
Dk(通道选择),然后验证在该特定检测器的响应映射
D
k
D^k
Dk的位置
(
i
,
j
)
(i,j)
(i,j)上是否有一个局部最大值。
Soft feature detection
在训练过程中,上述的硬检测程序被软化,以便于反向传播。首先,我们定义了一个软的局部最大值。得分
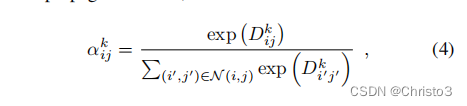
其中
N
(
i
、
j
)
N (i、j)
N(i、j)是像素
(
i
、
j
)
(i、j)
(i、j)(包括自身)的9个邻居的集合。然后,我们定义软通道选择,它计算一个最大比值。每个模拟通道级非最大抑制的描述符:
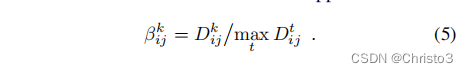
接下来,为了考虑到这两个标准,我们在所有特征图k上最大化这两个分数的乘积,以获得一个单一的得分图:
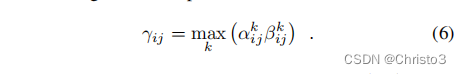
最后,通过进行图像级归一化,获得一个像素
(
i
,
j
)
(i,j)
(i,j)处的软检测分数
s
i
j
s_{ij}
sij:
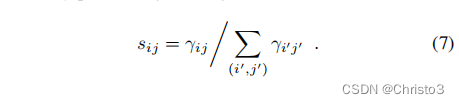
Multiscale Detection
虽然CNN描述符由于数据增强的预训练而具有一定的尺度不变性,但它们对尺度变化本身并不是不变性,在观点有显著差异的情况下,匹配往往失败。为了获得对尺度变化更稳健的特征,我们建议使用图像金字塔[2],就像通常在手工制作的局部特征探测器[28,30,32]或甚至对某些对象探测器[16]中所做的那样。这只在测试期间执行。
给定输入图像
I
I
I,构造一个包含三种不同分辨率
ρ
=
0.5
、
1
、
2
ρ = 0.5、1、2
ρ=0.5、1、2(对应于半分辨率、输入分辨率和双分辨率)的图像金字塔
I
ρ
I^ρ
Iρ,并用于提取每个分辨率下的特征图
F
ρ
F^ρ
Fρ。然后,将较大的图像结构从低分辨率特征图传播到高分辨率特征图,传播方式如下:
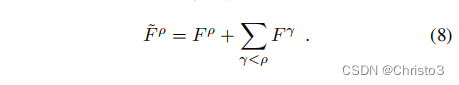
注意,特征映射
F
ρ
F^ρ
Fρ有不同的分辨率。为了实现(8)中的求和,使用双线性插值法将特征图
F
γ
F^γ
Fγ的大小调整到
F
ρ
F^ρ
Fρ的分辨率。通过将上述后处理应用于融合的特征图
F
ρ
F^ρ
Fρ来获得检测。为了防止重新检测特征,我们使用了以下响应门控机制:从最粗的尺度开始,我们标记检测到的位置;这些掩模被上采样(最近邻)到下一个尺度的分辨率;进入标记区域的检测被忽略。
2.2 4. Jointly optimizing detection and description
Training loss
为了训练所提出的模型,它使用一个单一的CNN
F
F
F来进行检测和描述,我们需要一个适当的损失
L
L
L来共同优化检测和描述目标。在检测的情况下,我们希望关键点在视点或照明的变化下是可重复的。在描述的情况下,我们希望描述符是独特的,以便它们不会不匹配。为此,我们提出了一个扩展的三重边际排名损失,它已成功地用于描述符学习[6,35],以解释检测阶段。我们将首先回顾三重边际排名损失,然后提出我们的联合检测和描述的扩展版本。
给定一对图像
(
I
1
,
I
2
)
(I_1,I_2)
(I1,I2)和它们之间的对应
c
:
A
↔
B
c: A↔B
c:A↔B(其中
A
∈
I
1
A∈I_1
A∈I1,
B
∈
I
2
B∈I_2
B∈I2),我们的三重边际排名损失寻求最小化相应描述符的距离
d
^
A
(
1
)
\hat{\mathbf{d}}_A^{(1)}
d^A(1)和
d
^
B
(
2
)
\hat{\mathbf{d}}_B^{(2)}
d^B(2)同时最大化与其他混杂描述符的距离
d
^
N
1
(
1
)
\hat{\mathbf{d}}_{N_{1}}^{(1)}
d^N1(1)和
d
^
N
2
(
2
)
\hat{\mathbf{d}}_{N_{2}}^{(2)}
d^N2(2)在这两种图像中,这可能的存在是由于类似的图像结构。为此,我们将相应描述符之间的正描述符距离
p
(
c
)
p (c)
p(c)定义为:
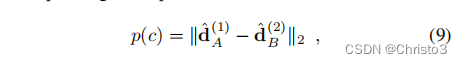
负距离
n
(
c
)
n (c)
n(c),它解释了其中一个最混杂的描述符
d
^
A
(
1
)
\hat{\mathbf{d}}_A^{(1)}
d^A(1)和
d
^
B
(
2
)
\hat{\mathbf{d}}_B^{(2)}
d^B(2),定义为:
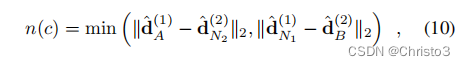
其中,负样本
d
^
N
1
(
1
)
\hat{\mathbf{d}}_{N_{1}}^{(1)}
d^N1(1)和
d
^
N
2
(
2
)
\hat{\mathbf{d}}_{N_{2}}^{(2)}
d^N2(2)是位于正确对应的平方局部邻域之外的最大负样本:
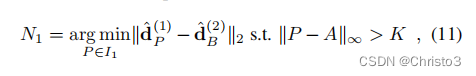
对于n2也是如此。边际M的三重边际排名损失可以定义为:
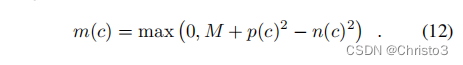
直观地说,这种三重边际排名损失试图通过惩罚任何可能导致错误匹配分配的混淆描述符来加强描述符的独特性。为了进一步寻求检测的可重复性,我们以以下方式在三重边际排名损失中添加了一个检测项:
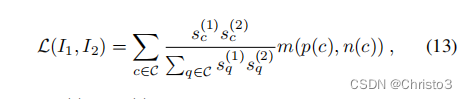
式中,
s
c
(
1
)
s_c^{(1)}
sc(1)和
s
c
(
2
)
s_c^{(2)}
sc(2)分别为
I
1
I1
I1和
I
2
I2
I2中A点和B点的软检测分数(7),C为
I
1
I_1
I1和
I
2
I_2
I2之间所有对应关系的集合。建议的损失基于其检测分数产生所有匹配的边际项m的加权平均值。因此,为了使损失最小化,最独特的对应项(具有较低的边际项)将获得较高的相对得分,反之亦然——相对得分较高的对应项被鼓励使用与其他对应项相似的描述符。
3 结论










![[2.1.4]进程管理——进程通信](https://img-blog.csdnimg.cn/img_convert/85bde92bfbe00fc5958c9a68b3130eee.png)
