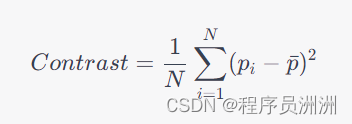2021年第十一届MathorCup高校数学建模

D题钢材制造业中的钢材切割下料问题

原题再现

某钢材生产制造商的钢材切割流程如图 1 所示。其中开卷上料环节将原材料钢卷放在开卷机上，展开放平送至右侧操作区域（见图 2）。剪切过程在剪切台上完成，剪切台上依次有切头剪和圆盘剪。
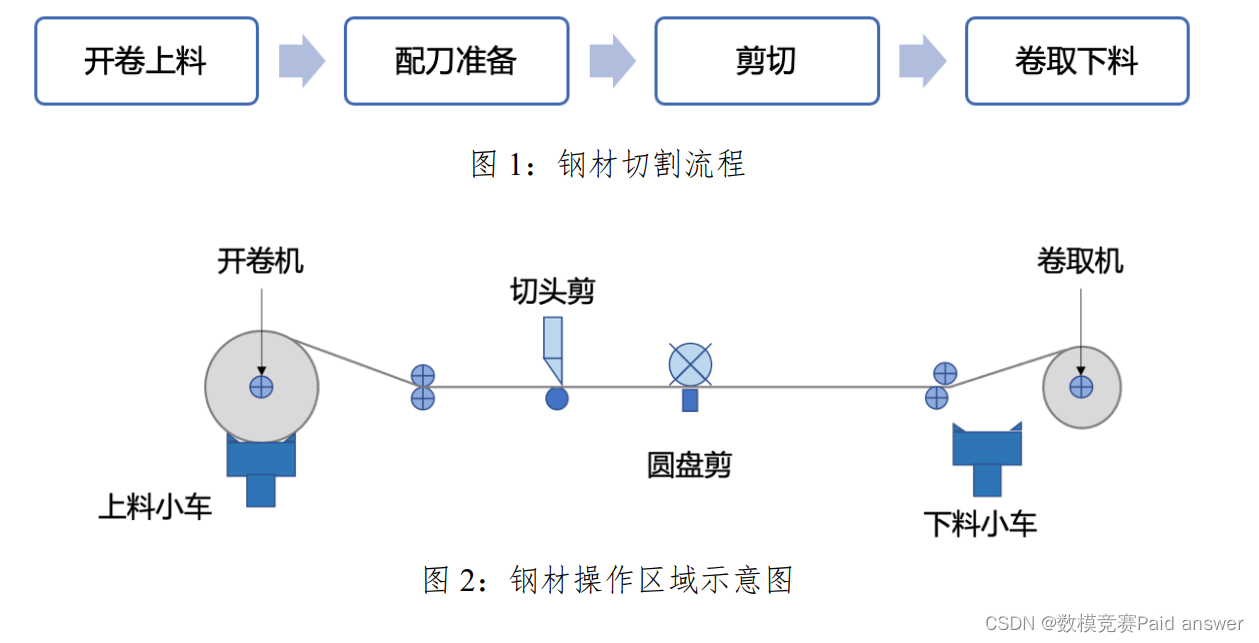
在这里插入图片描述
圆盘剪（见图 3）用旋转的圆盘刀片连续对纵向运动着的原材料进行切割。在圆盘剪剪切前，需根据订单切割方案进行排刀。假设排刀架上可以以任意间距排刀，但刀具数量是有限制的，一次排刀上限不能超过 5 刀。用同一排刀方案切割得到的订单称为一组订单，切割不同组时需要工人重新排刀，称为一次换刀。切割每卷原材料之间均需要换刀。切头剪为“一刀切”，即将整个钢板横向完全切断。图 4-1 中的横向切割（红色虚线所示）不满足一刀切要求，无法用切头剪实现，图 4-2 的横向切割（红色虚线所示）则符合要求。

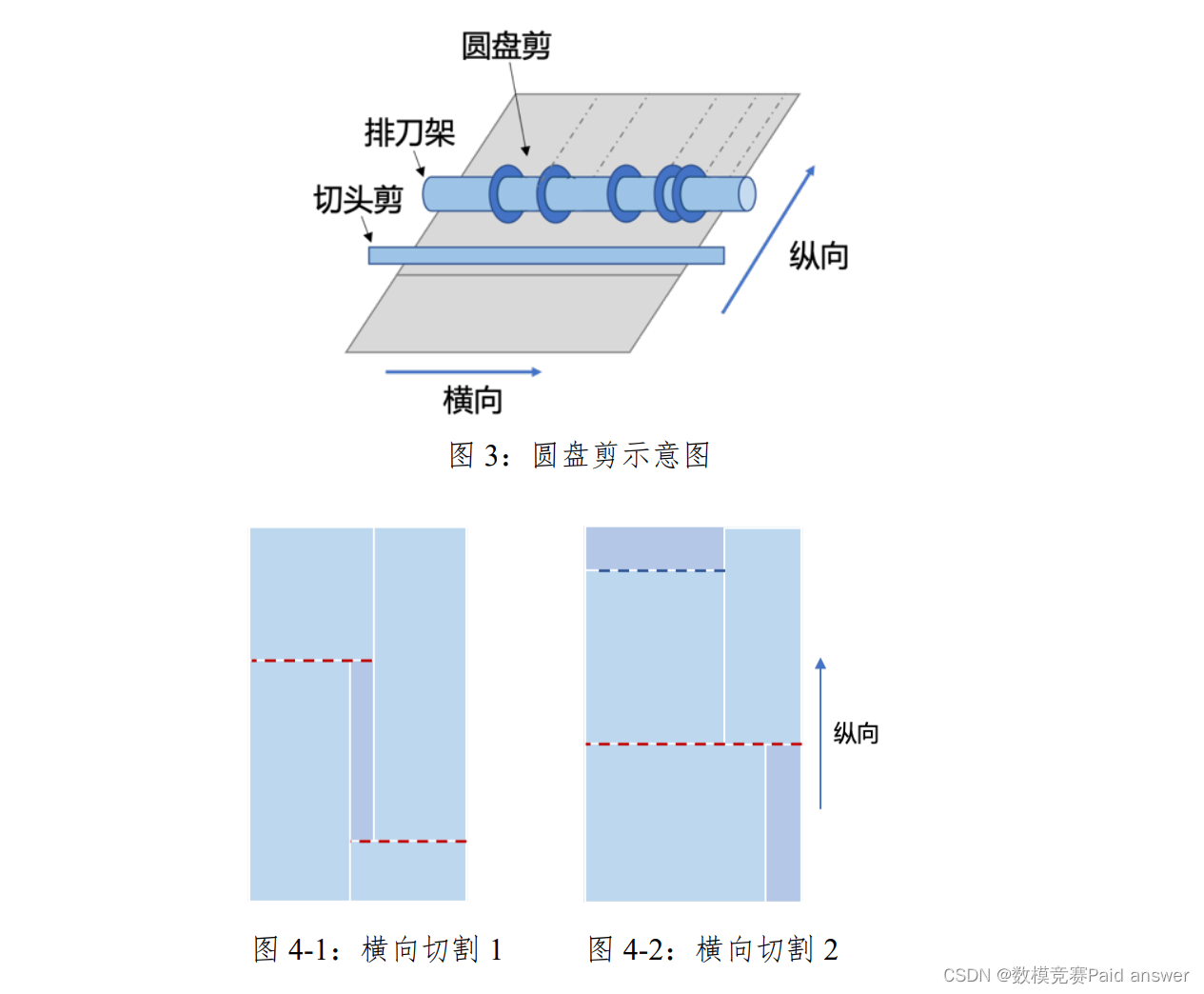
在这里插入图片描述
经过横向切割后，当且仅当某些订单还需要额外横向一刀将其与废料分开，则将这些订单移至小机器再次切割（见图 4-2 蓝色虚线）。同一组内相同订单可以通过一刀同时变成成品。钢材切割订单有两种，分别是板料订单和卷料订单。切完的板料订单直接通过下料小车包装入库，卷料则需要先通过卷取机压臂成卷再入库。
原料在切割成品的同时若有剩余，且符合余料标准（见附件 2），则可将这部分按照余料标准回收入库，供下次切割使用。不符合余料标准的称为废料，必须丢弃。成材率定义为，被切割成成品的面积加上可回库的余料面积与使用原料总面积之比。

更详细的切割说明可参考附件 1 某原材料切割方案说明.xlsx。
工厂未来一批订单需求已给出，订单需求数量必须恰好满足（不允许超额供应）。根据工厂现有原料切割订单，每种原料的使用数目不能超过其库存。请建立数学模型解决下面的问题。
问题 1：针对给出的所有原料，请使用最少张数的原材料，满足对 5种卷料的要求（不考虑浮动比例），同时尽量提高总的成材率，给出切割方案。
问题 2：针对给出的所有原料，请使用最少张数的原材料，满足对所有订单的要求（不考虑浮动比例），同时尽量提高总的成材率，给出切割方案。
问题 3：圆盘剪每次排刀需要人工更换刀在排刀架上的位置，同时若有材料需要被移到小机器上再次切割也需要人为操作。为减少人力成本，希望尽量减少换刀数和在小机器上切割数。针对给出的所有原料，请使用最少张数的原材料，满足对所有订单的要求（不考虑浮动比例）。同时尽量减少换刀数和在小机器上切割数，并尽量提高总的成材率。给出切割方案。
问题 4：若订单额外指定了浮动比例，则交付的订单长度可在需求长度的基础上上下浮动。例如，规定浮动比例为 5%，则切割出的长度在原有长度的 95%到 105%之间均满足要求。请重新按照第 2 问的要求，给出切割方案。
另外，请在完成论文基础上，将每问切割方式信息填入“提交结果.xlsx”文件对应表单中。

整体求解过程概述(摘要)

根据订单的要求，工厂要用 10 种不同的原材料切割成 15 种不同规格的订单。故该原料切割问题为典型的优化模型。在切割过程中，要求使用的原料张数尽可能少，同时提高成才率。故针对不同的订单需求及切割条件要求，得出 4 种相应的最佳切割方案。
问题一要求使用张数最少，同时要提高成材率。在满足五种卷料订单的基础上，尽可能的使用面积较大的原材料。故先将原料面积按降序排列，使用线性规划找出最佳宽度的材料匹配，先进行进行较大面积的原料切割，以此来减少使用张数，并求得最少原材料张数为 22 张。
问题二在问题一的要求上加上了 10 种板料的订单。根据板料的规格大小来看，板料长度普遍较短，可以充分利用切割卷料后的余料进行相应的切割，从而达到减少使用张数，并求得最少原材料张数为 22 张。
问题三在原有要求上增加了减少人为操作次数的要求，为减少排刀次数和小机器切割次数，要在同一张原料切割出尽可能多的相同订单，并直接将余料入库回收，不做二次切割，按照减少使用张数和减少人为操作进行整体线性规划。从而找出最佳切割方案，求得最少认为操作次数为 42 次。
问题四指出部分订单在长度上存在不同的浮动比例，使问题更加接近实际操作情况。针对不同订单的浮动比例，充分考虑所有的浮动情况太过复杂。利用 random 函数生成随机的浮动比例，将生成的浮动比例带入到数学模型中进行相应计算，得出最佳切割方案。其余范围内变化的浮动比例况均可类比此种方法得出切割方案。

模型假设：

（1）假设切割过程中不会有原料损耗。
（2）假设切割所得订单均为合格品。
（3）假设排刀时不发生人为错误。
（4）假设卷料在通过卷取机压臂成卷的过程中不存在长度和宽度的变化。
（5）假设符合长度和宽度的剩余原料即可作为余料，不考虑其他形变等因素。

问题分析：

问题一的分析

问题一要在给出的所有原料中，使用最少的原料张数，满足五种卷料的订单方案，并尽可能提高成材率。订单的长、宽与原材料的长、宽是双向选择的关系。对于多变量且变量与变量相互影响的问题，通常采用以一个变量为研究对象，固定其他变量，从而找到最优解的方法。对于此题，订单的长与宽两个变量是固定组合变换，可视为一个变量，原材料的长与宽同理也可以视为同一变量。选择订单长为固定变量或订单宽为固定变量都可以将多变量问题转换为单变量问题从而求解。若采取将订单长作为固定变量，则先按照订单长度将订单在原材料上纵向排开；若采取将订单长作为固定变量，则先按照订单宽度将订单在原材料上横向排开。为使所需的原材料张数最小，将原材料按面积进行从大到小排序，面积越大，则所能制作的订单越多，所需要的张数就越小。大面积订单选择大面积原料进行切割，小面积订单选择小面积原料进行切割，会使得面积利用率较高，故对订单进行同样的排序操作。由于卷料订单长度普遍较长，对于问题一可筛除长度小于订单长度最小值的原料，从而减少算法运算量。面积匹配后，按照固定订单长或固定订单宽的方法依次排放订单，即可求出排刀方案以及所需的订单张数。

问题二的分析

在问题一的基础上，除五种卷料订单，另外加上 10 种板料订单。不同于问题一，板料订单长度普遍较小，故不存在原料长度小于订单长度最小值的情况，需要将所有原料都考虑在内。并且在问题一中，符合标准的余料都不能满足卷料订单的需求，而在问题二中进行卷料切割时会产生较多符合标准并且能够满足板料的余料，将余料做为新的一种原料进行优先切割来满足板料，从而提高成材率并减少使用的原料张数。

问题三的分析

在问题二的基础上，考虑排刀次数以及小机器切割数的情况，为尽可能减少排刀次数，在使用一张原材料时尽可能不更换订单的排列，同时让排在原料末尾的订单尽量相同从而减少小机器切割数。问题二中为减少使用原料张数而将余料进行二次切割，而针对问题三，对余料进行二次切割会增加人工排刀次数以及小机器切割数，故对于问题三要放弃对余料的二次切割从而降低排刀次数以及小机器切割次数。

问题四的分析

在问题二的基础上，考虑指定的浮动比例的情况，更加符合钢材制造的过程中的实际情况。在订单需求表里给出了七种订单的浮动比，由于七种订单规格不同，浮动比也不同，这里固定七种订单的浮动比，固定订单宽度将订单在原料上进行排刀，再利用所建模型进行数据处理求得最终解。其他变化的浮动比可代入模型中求解，利用随机数生成范围内的浮动比即可代入求解。

模型的建立与求解整体论文缩略图

在这里插入图片描述

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

The actual procedure is shown in the screenshot

import copy
yL=[148623.91,32960.49,75508.72,14091.52,75040.31,138570.39,98641.28,114074.
27,104637.72,58023.82]
yW=[1519.91,999.35,1232.32,920.62,1573.71,844.99,1184.54,879.02,969.02,1785.
45]
yN=[5,10,8,2,3,10,12,9,3,10]
dL=[44351.13,39229.01,54787.74,45284.39,53479.79,897.32,896.09,1096.33,890.
53,422.88,970.16,998.29,1024.87,621.91,1243.03]
dW=[422.88,282.88,268.36,277.70,332.29,603.06,714.72,435.84,343.08,641.45,6
67.21,472.30,340.51,476.60,471.25]
dN=[36,29,42,32,18,38,23,31,40,42,34,25,24,22,28]
yS=[]
dS=[]
for i in range(0,10):
yS.append([yL[i]*yW[i],yL[i],yW[i],yN[i],i+1])
for i in range(0,5):
dS.append([dL[i]*dW[i],dL[i],dW[i],dN[i],i+1])
y = sorted(yS, key=(lambda x: [x[0],x[1], x[2],x[3],x[4]]))
d = sorted(dS, key=(lambda x: [x[0],x[1], x[2],x[3],x[4]]))
y.reverse()
d.reverse()
y2=copy.deepcopy(y)
d2=copy.deepcopy(d)
result=1
n=0
x=0
k=y[n][2]
p1=[]
p2=[]
p3=[]
z=0
sd=0
sy=0
for i in range(0,5):
for j in range(0,d[i][3]):
z=z+1
sd=sd+d[i][0]#算成材率
p1.append(d[i][4])
if y[n][2]<d[i][2]:
p1.pop()
p2.append(p1)
p1=[d[i][4]]
if j==0:
y[n][1]=y[n][1]-d[i-1][1]
else:
y[n][1]=y[n][1]-d[i][1]
if y[n][1]>=d[i][1]:
y[n][2]=y2[n][2]
y[n][2]=y[n][2]-d[i][2]
elif y[n][1]<d[i][1]:
sy=sy+y[n][0]#算成材率
p3.append(p2)
p3.append(y[n][4])
p2=[]
y[n][3]=y[n][3]-1
result=result+1
if y[n][3]==0:
n=n+1
y[n][2]=y[n][2]-d[i][2]
else:
y[n][1]=y2[n][1]
y[n][2]=y2[n][2]-d[i][2]
else:
y[n][2]=y[n][2]-d[i][2]
if i==4 and j==(d[i][3]-1):
p2.append(p1)
p3.append(p2)
p3.append(y[n][4])
c=sd/sy
print(result,p3,c)

import copy
yL=[148623.91,32960.49,75508.72,14091.52,75040.31,138570.39,98641.28,114074.
27,104637.72,58023.82]
yW=[1519.91,999.35,1232.32,920.62,1573.71,844.99,1184.54,879.02,969.02,1785.
45]
yN=[5,10,8,2,3,10,12,9,3,10]
dL=[44351.13,39229.01,54787.74,45284.39,53479.79,897.32,896.09,1096.33,890.
53,422.88,970.16,998.29,1024.87,621.91,1243.03]
dW=[422.88,282.88,268.36,277.70,332.29,603.06,714.72,435.84,343.08,641.45,6
67.21,472.30,340.51,476.60,471.25]
dN=[36,29,42,32,18,38,23,31,40,42,34,25,24,22,28]
yuL=[15570.52,15570.52,15570.52,15570.52,41664.33,38498.65,2717.22,2717.22,
2717.22,6055.74,14127.53,20183.26,20183.26,21560.52,20252.57,2899.491,2899.
491,2899.491,2899.491,2899.491,2899.491,20193.26]
yuW=[1268.64,1268.64,1268.64,1268.64,1382.96,844.99,844.99,844.99,844.99,63
0.54,630.54,1184.54,1184.54,664.58,806.64,805.08,805.08,805.08,805.08,805.0
8,805.08,1184.54]
yuB=[1,1,1,1,12,6,62,62,62,7,72,73,73,5,52,63,63,63,63,63,63,74]
yuN=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
yS=[]
dS=[]
yuS=[]
for i in range(0,22):
yuS.append([yuL[i]*yuW[i],yuL[i],yuW[i],yuN[i],yuB[i]])
for i in range(0,10):
yS.append([yL[i]*yW[i],yL[i],yW[i],yN[i],i+1])
for i in range(0,15):
dS.append([dL[i]*dW[i],dL[i],dW[i],dN[i],i+1])
y = sorted(yS, key=(lambda x: [x[0],x[1], x[2],x[3],x[4]]))
d = sorted(dS, key=(lambda x: [x[0],x[1], x[2],x[3],x[4]]))
yu = sorted(yuS, key=(lambda x: [x[0],x[1], x[2],x[3],x[4]]))
y.reverse()
d.reverse()
yu.reverse()
z=0
for i in yu:
y.insert(3+z,i)
z=z+1
del y[0]
del y[0]
del y[0]
y2=copy.deepcopy(y)
d2=copy.deepcopy(d)
yu2=copy.deepcopy(yu)
result=0
n=0
x=0
k=y[n][2]
p1=[]
p2=[]
p3=[]
z=0
sd=0
sy=0
for i in range(5,15):
for j in range(0,d[i][3]):
z=z+1
sd=sd+d[i][0]#算成材率
p1.append(d[i][4])
if y[n][2]<d[i][2]:
p1.pop()
p2.append(p1)
p1=[d[i][4]]
if j==0:
y[n][1]=y[n][1]-d[i-1][1]
else:
y[n][1]=y[n][1]-d[i][1]
if y[n][1]>=d[i][1]:
y[n][2]=y2[n][2]
y[n][2]=y[n][2]-d[i][2]
elif y[n][1]<d[i][1]:
sy=sy+y[n][0]#算成材率
p3.append(p2)
p3.append(y[n][4])
p3.append(y2[n][2])
p2=[]
y[n][3]=y[n][3]-1
if n>21:
result=result+1
if y[n][3]==0:
n=n+1
y[n][2]=y[n][2]-d[i][2]
else:
y[n][1]=y2[n][1]
y[n][2]=y2[n][2]-d[i][2]
else:
y[n][2]=y[n][2]-d[i][2]
if i==14 and j==(d[i][3]-1):
p2.append(p1)
p3.append(p2)
p3.append(y[n][4])
c=sd/sy
print(result,p3,c)