外观以及性质：

Propargyl α-D-Mannopyranoside一般为白色粉末状，糖化学类产品比较多，一般包括：葡萄糖衍生物、葡萄糖醛酸衍生物，氨基甘露糖衍生物、半乳糖衍生物、氨基半乳糖衍生物、核糖衍生物、阿拉伯糖衍生物、唾液酸衍生物等一系列的。

Propargyl α- D-mannopyranoside is generally white powder, and there are many sugar chemical products, generally including glucose derivatives, glucuronic acid derivatives, aminomannose derivatives, galactose derivatives, aminogalactose derivatives, ribose derivatives, arabinose derivatives, sialic acid derivatives and a series of other derivatives.

【产品理化指标】：

中文名：炔丙基 α-D-吡喃甘露糖苷

英文名：Propargyl α-D-Mannopyranoside

CAS号：854262-01-4

分子式：C9H14O6

分子量：218.2

性 状：白色粉末

供应商：西安凯新生物科技有限公司

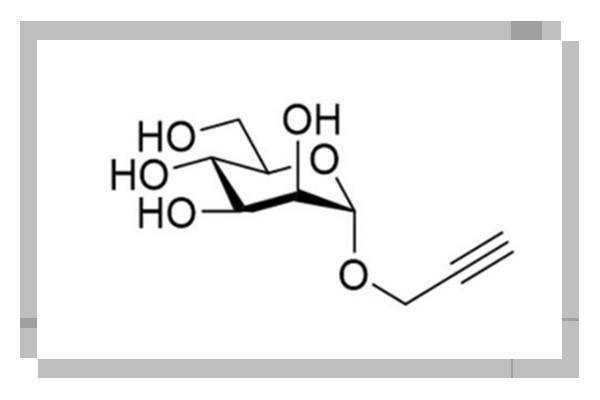
Propargyl α-D-Mannopyranoside结构式：

规格包装：1g，5g，10g，接受各种复杂PEGS定制服务，具体可以线上咨询商家

溶解性：溶于大部分有机溶剂，如：DCM、DMF、DMSO、THF等等，在水中有很好的溶解性

【注意事项】：

1、本品应密封避光，储存于阴凉，干燥，通风处。

2、避免频繁解冻，现配现用，-20℃以下冰冻

3、仅用于科学研究或者工业应用等非医疗目的，非药用，非食用

【相关试剂类产品】

CAS：1399861-03-0 ，中文名： ε-N-巴豆酰基赖氨酸

CAS：1131610-84-8 ，中文名：4-甲基苯基 β-D-硫代呋喃核糖苷

CAS：19879-84-6 ，中文名：2,3,4,6-四-O-乙酰基-β-D-硫代吡喃葡萄糖

CAS：494-08-6 ，中文名：4-(β-D-葡萄糖氧基)-3-甲氧基苯醛

CAS：134253-42-2 ，中文名： 1-O-甲基-β-D-葡萄糖醛酸钠盐

CAS：1030262-99-7 ，中文名： 2-(4-戊炔酰氨基)-2-脱氧-D-吡喃葡萄糖

CAS：854262-01-4 ，中文名：中文名： 炔丙基 α-D-吡喃甘露糖苷

CAS：1658458-26-4 ，中文名： Ac4GalNAl

CAS：159610-92-1 ，中文名： 6-azido-L-norleucine

CAS：1418009-93-4 ，中文名：6-Azido-D-lysine HCl

CAS：13100-46-4 ，中文名： 1,2,3,4-四-O-乙酰基-β-D-吡喃葡萄糖

CAS：34301-54-7 ，中文名： 1-金刚烷硫醇

CAS：653600-56-7 ，中文名：Ac4GaINAz

CAS：120791-76-6 ，中文名：N-(芴甲氧基羰基)-L-苏氨酸叔丁酯

CAS：80321-89-7 ，中文名： 1,3,4,6-四-O-乙酰基-2-叠氮-2-脱氧-β-D-吡喃葡萄糖

CAS：342640-42-0 ，中文名： 苄基 2-叠氮基-3,6-二-O-苄基-2-脱氧-β-D-吡喃葡萄糖苷

CAS：857677-98-6 ，中文名：1,3,4,6-四-O-乙酰基-2-脱氧-2-[(2-叠氮乙酰基)氨基]-β-D-吡喃葡萄糖

CAS：120173-57-1 ，中文名：N-芴甲氧羰基-O-(2-乙酰氨基-3,4,6-三-O-乙酰基-2-脱氧-α-D-吡喃半乳糖基)-L-丝氨酸

CAS：352008-11-8 ，中文名：乙基 4,6-O-苯亚甲基-3-O-(2-甲基萘基)-2-O-苯甲酰基-β-D-硫代吡喃葡萄糖苷