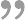三、数据存储

3.1 数据类型

计算机行业中使用术语“多媒体”来定义包含数字、文本、音频、图像和视频的信息。

位：bit，binary digit的缩写，是存储在计算机中的最小单位，它是0或1.

位模式：为了表示数据的不同类型，应该使用位模式，它是一个序列，有时也称为位流。通常8位的位模式称为1字节。有时用字这个术语指代更长的位模式。属于不同数据类型的数据可以以同样的位模式存储在内存中。

3.2 存储数字

数字在被存储到计算机之前，都要先转换成二进制。对于小数点，计算机有两种表示法：定点和浮点。定点用来存储整数，浮点用来存储实数。

3.2.1 存储整数

整数可以被当作小数点位置固定的数字：小数点固定在最右边。因此，定点表示法用来存储整数，在这种方法中，小数点是假定的，并不存储。

3.2.1.1 无符号表示法

只包括0和非负整数。如果计算机分配用于存储无符号整数的位数为 $n$ ，那么所能存储的最大无符号整数为 $2^{n}-1$ 。

在存储无符号整数时，先将整数变为二进制数，如果二进制数不足 $n$ 位，则在前面补0，如果大于 $n$ 位，该整数无法存储，发生溢出。

因为存储单元数量的限制，所能存储的最大无符号整数是有限制的，这个值为 $2^{n}-1$ 。当大于这个值的数存储时，就会发生溢出。

应用：记数、寻址、存储其他数据类型。

3.2.1.2 符号加绝对值表示法

尽管符号加绝对值表示法在储存整数时不常见，但该格式用于在计算机中存储部分实数以及采样模拟信号等。

在这种方法中，用于无符号整数的有效范围被分成两个相等的部分，前半个表示正数，后半部分表示负数。在这种方法中，二进制最左边的位表示数字的正负，0表示正，1表示负，有两个0 $\left ( +0,-0 \right )$ 。

该方法有正负两种溢出情况，存储过大过小的数字都会产生溢出。

3.2.1.3 二进制补码表示法

几乎所有的计算机都使用二进制补码来存储整数。在这种方法中，二进制最左位的0表示正数，1表示负数。

反码：将一个整数的二进制码按位取反（0变为1，1变为0）得到的结果就是该二进制码的反码。

补码：有两种方法。第一种：从右边复制位，直到有1被复制，再取反其余位。第二种：将原码取反，再加1.

补码有两种理解方法：

第一种：将负数看成正数的负值。在存储整数时，不论正负，先将其转换成其绝对值的二进制码，如果是正数，以原样存储，如果是负数，则取原码的补码进行存储（按照上面的方法取补码）。在将二进制还原整数时，首先看符号位确定其符号，如果为0，则将二进制转换为10进制再加正号，如果为1，先取补码再转换为10进制，再加负号。

第二种：将正数和其负值看作两个数。在存储时，先按照符号加绝对值法写出其二进制码，如果为正数，按原样存储，如果为负数，则符号位不变，其余位取反加1，然后存储。从二进制还原时，如果为正数，则直接转换，如果为负数，符号位不变，其余位按位取反加1，并转换成十进制。

二进制补码也有正负两种溢出。

三种方法的比较：

3.2.2 存储实数

实数是带有整数部分和小数部分的数字。如果使用定点法，对于 $n$ 位的存储单元来说，不论怎样给整数和小数部分各自分配空间，都会出现无法存储很大的数（分配给小数部分的空间过多）或是无法存储很小的数（分配给整数部分空间过多）的情况。参考科学计数法，在计算机中使用浮点来存储实数。

浮点表示法：使用浮点表示法可以维持实数存储的正确度和精度。该方法允许小数点浮动：可以在小数点左右有不同的数码。使用这种方法可以存储很大或很小的实数。

一个数字的浮点表示法由三部分组成：符号、位移量和定点数。

浮点表示法在科学研究中用来表示很大或很小的数，小数点左边只有一个位，并且位移量是10的幂。

规范化：为了使表示法的固定部分统一，科学计数法（十进制）和浮点表示法（二进制）都在小数点左边使用了唯一的非零数码，这称为规范化。显然，在二进制中，小数点左边的一位非零数码只能是1，这也就说明，我们只需要存储规范化后的小数部分，因为所有规范化后的二进制实数的整数部分都为1.

符号、指数和尾数：在二进制数规范化后，我们只需要存储一个数的符号、指数和尾数（小数点右边的位）。符号：用一位来存储（0或1）。指数：小数点移动的位数，可正可负，用余码表示法。尾数：小数点右边的位，作为无符号整数来存储，尾数是小数，只是以无符号整数的形式来存储。

余码系统：指数是有符号的数，尽管可以使用二进制补码来存储，但被一种称为余码系统的新的表示法所取代。在余码系统中，正数和负数都可以作为无符号整数存储。为了表示正的或负的整数，一个正整数（称为偏移量）加到每个数字上，将它们统一移到非负的一边。这个偏移量的值是 $2^{m-1}-1$ ， $m$ 是用来存储指数的内存单元的大小。

IEEE标准：电气和电子工程师协会已定义了几种存储浮点数的标准。我们讨论最常用的两种——单精度和双精度。

IEEE标准存储浮点数：

1. 在S中存储符号（0或1）

2. 将十进制转换成二进制

3. 规范化

4. 确定E（指数）和 M（尾数）的值

5. 连接S、E、M。

将存储位IEEE标准的实数还原：

1. 找到S、E、M的值

2. 由S确定符号

3. 找到位移量（E-127）

4. 去规范化

5. 将二进制转换成十进制

6. 加上符号

上溢和下溢：当存储的数字（绝对值）过小时会发生下溢（指数溢出），当存储数字（绝对值）过大时会发生上溢（指数溢出）。

存储零：将所有位都置零。

截断错误：当规范化后小数点右边的位数过多时，会截断掉右边超出存储范围的部分，这种原始数字与还原后数字的差异称为截断错误。当这种错误出现在宇航等领域的计算中时，后果是很严重的，这时需要使用更大的尾数表示法。

3.3 存储文本

在任何语言中，文本的片段是用来表示该语言中某个意思的一系列符号，也就是说，文本是符号的集合，要存储文本就要存储这些符号。文本中的符号可以是标点、英文字母、汉字等。

使用不同的位模式来表示不同的符号，这样文本就可以作为符号的集合存储在计算机中。表示符号的过程被称为编码。

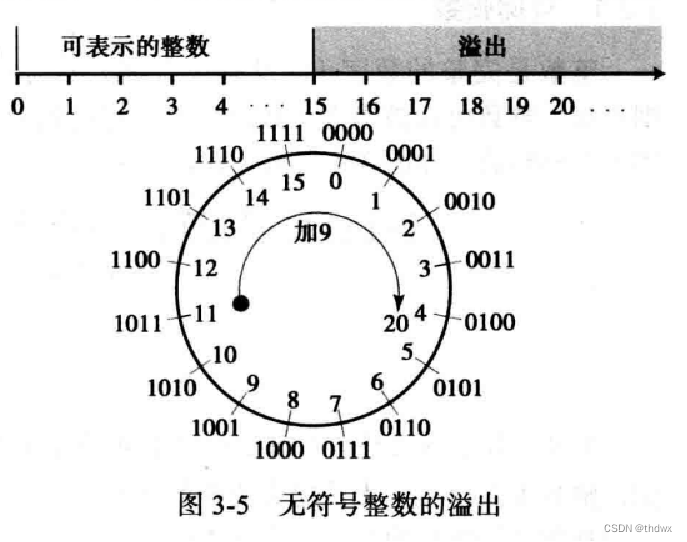
ASCII：美国国家标准协会开发了一个被称为美国信息交换标准码的编码。该编码使用7位表示每个符号，可以定义128种不同的符号。如今ASCII是Unicode的一部分。

Unicode：这种编码使用32位，最大能表示4294967296个符号。编码的不同部分被分配用于表示来自世界上不同语言的符号，还有些部分被用于图形和特殊符号。

3.4 存储音频

文本中的符号是可以记数的，但音频是随声音变化的实体，我们只能记录声音在某一时刻的密度。音频是模拟数据的例子。

采样：如果不能记录一段时间中音频的所有值，至少可以记录其中的一部分。采样意味着我们在模拟信号上选择数量有限的点来度量它们的值并记录下来。采样率指单位时间内采取样本的数量。

量化：将样本的值截取为最接近的整数（方便存储）。如，实际值为17.2，截取为17；实际值为17.8，可截取为18.

每样本位：记录每个样本分配的位数，有时称为位深度。

位率：如果位深度或每样本位为B，采样率为S，则位率为 B*S，即每秒样本需要的空间大小。

编码：当今音频编码的主流标准是MP3（MPEG Layer 3的简写）。它采用每秒44100个样本，每样本16位。

3.5 存储图像

3.5.1 光栅图（位图）

一张照片由模拟数据组成，类似音频，不同的是，数据密度随空间变化。这意味着数据需要采样。这种采样通常被称为扫描，样本称为像素。也就是说，图片被分为很小的像素，每个像素都有单独的密度值。

解析度：每英寸的方块或线条记录的像素数量。在图像处理中的扫描率被称为解析度。如果解析度够高，人眼就看不出重现图像中的不连续。

色彩深度：用于表现像素的位的数量。依赖于像素的颜色是由何种不同的编码技术来处理的。真彩色：使用24位来编码一个像素，每个三原色（RGB）占8位（0-255）。索引色：许多应用程序并不会用到如此大量的颜色，选择其中的一部分并进行编码，每个像素8位。

编码：JPEG（联合图像专家组）使用真彩色模式，但压缩图像来减少位的数量。GIF（图形交换格式）使用索引色模式。

3.5.2 矢量图

光栅图有两个缺点：文件体积太大、重新调整图像大小有麻烦。放大光栅图意味着扩大像素，所以放大后的图像看起来很粗糙。矢量图图像编码方法并不存储每个像素的位模式，而是将图像分为几何图形的组合，如线段、圆等，每个几何图形由数学公式表达。矢量图是由定义如何绘制这些几何图形的一系列命令构成的。

当要显示或打印图像时，将图像的尺寸作为输入传入给系统，系统重新设计图像的大小并用相同的公式画出图像。

矢量图不适合存储照片图像的细微精妙。JPEG或GIF光栅图提供了更好和更生动的图片。矢量图可以用于创建字体、工程绘图等。

3.6 存储视频

视频是图像（帧）在时间上的表示。一部电影就是一系列的帧一张接一张播放而形成运动的图像。换言之，视频是随空间（单个图像）和时间（一系列图像）变化的信息表现。所以，直到如何将一张图像存储在计算机中，也就知道如何存储视频：每一幅图像或帧转换成一系列位模式并存储。

四、数据运算

4.1 逻辑运算

4.1.1 位层次上的逻辑运算

非（NOT）：只有一个输入，输出与输入相反。

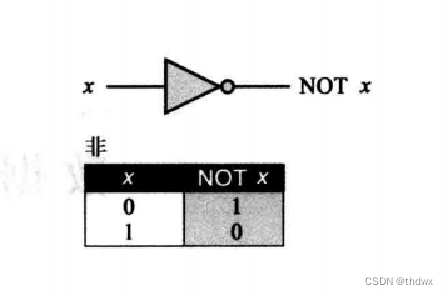
与（AND）：二元运算符，两个输入。输入都为1，则输出1，输入有0，则输出0.

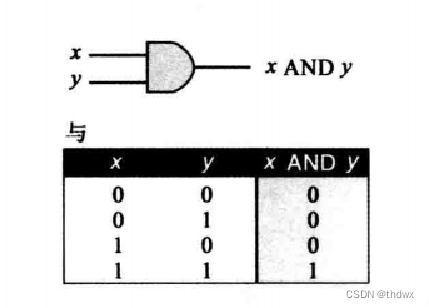
或（OR）：二元运算符，两个输入。输入都为0，则输出0，输入有1，则输出1.

异或（XOR）：二元运算符，两个输入。输入相同，输出为0；输入相异，输出为1.

4.1.2 模式层次的逻辑运算

相同的四个运算符可以被应用到 $n$ 位模式。模式层次的逻辑运算就是对模式的每一位进行对应的逻辑运算（位数相同的两个模式）。

应用：4种逻辑运算能够修改位模式。

求反：对位模式的每一位进行取反操作。

指定位复位：利用 “与” 运算，可以用一个位模式将另一个位模式的指定位复位为0.这个用来修改其他位模式的位模式就称为掩码（掩盖本来的位模式）。

指定位置位：利用 “或” 运算，可以将一个位模式的指定位置为1.

指定位反转：利用 “异或” 运算，可以将一个位模式的指定位反转。

4.2 移位运算

逻辑移位：应用于不带符号位的数的模式。逻辑右移将位模式中的每一位向右移动一位，最右边的位丢失，最左位补零；逻辑左移将位模式中的每一个位向左移动一位，最左位丢失，最右位补零。

循环移位：同逻辑移位相似，但没有位的丢失，右移时，最右位移到最左位；左移时，最左位移到最右位。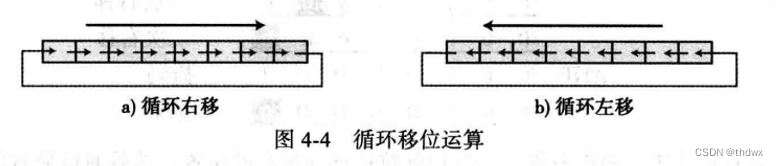

算数移位： 算术移位应用于二进制补码表示的带符号位的整数。算数左移（乘2）时，每移动一位，最左位丢弃，最右位补零，如果符号位没变，则运算成功，否则发生溢出；算数右移（除以2）时，最右位丢弃，最左位补原来的符号位。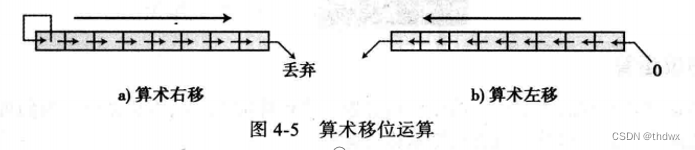

4.3 算术运算

算数运算包括加减乘除，适用于整数和浮点数。这里只讨论加、减。

整数的加减法：在大多数计算机中，整数都是以二进制补码的形式存储的，也就是说，在进行加减运算时，也是以补码的形式进行的。减法可以看作是和负数的加法。

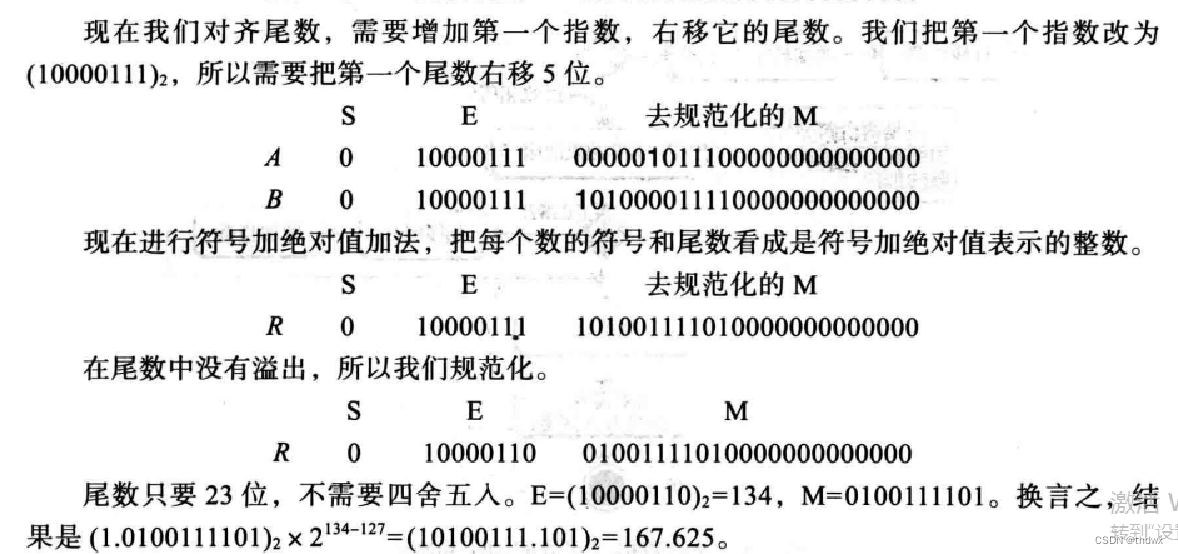
实数的加减法：

计算机科学导论笔记（二）