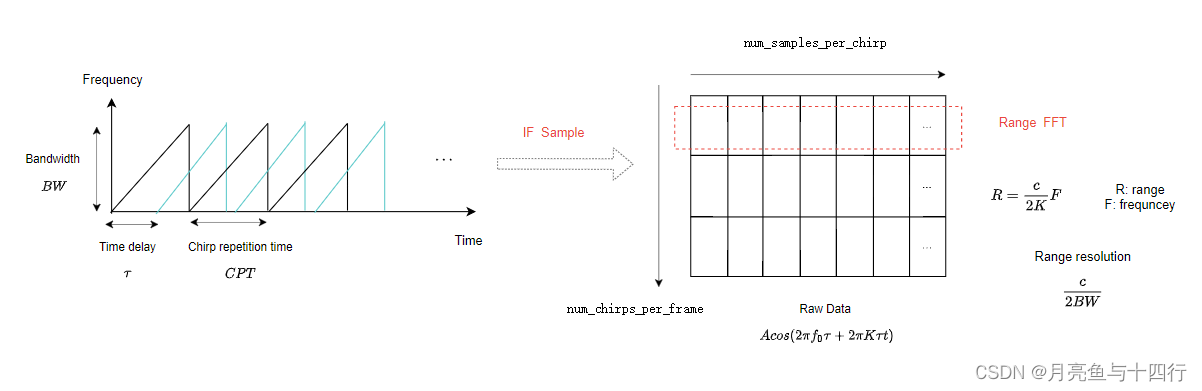
承接上篇博文 中频IF信号 ，我们已经知道得到的中频IF信号的形式为：

$$x_{IF}(t)=A^{\prime \prime }\cos (2\pi K\tau t+2\pi f_o\tau )$$

其中时延$\tau =\frac{2d}{c}$， $d$ 为探测目标的距离。

在实际中，我们对得到的IF信号进行ADC采样，即将模拟信号（analog signal）转换为数字信号（digital signal），然后对采样后的信号进行数字信号处理。

最大探测距离

假设ADC的采样率为$f_s$，采样点数为M，FFT点数为N（N≥M）。根据FFT频谱分析的知识，我们知道此时最大能分辨的频率分量为$\frac{f_s}{2}$。

对采样后的IF信号作FFT，即可完成对其的频谱分析，假设我们测得在频率 $f$ 处有一个峰值（peak），其就对应着在距离 $d$ 处有一个目标。即：

$$f_{peak}=K\tau =K\frac{2d_{target}}{c}$$

进行距离的换算，我们就有：

$$d_{target}=\frac{c}{2K}{f}_{peak}=\frac{c\cdot CRT}{2BW}{f}_{peak}$$

其中，CRT指的chirp重复的周期，即chirp repetition time，BW指的是chirp的扫频带宽，即band width。

现在我们看$f_{peak}$的取值范围。由于ADC的采样率为$f_s$，FFT点数为N，即是在频率轴上（$\frac{f_s}{2}\frac{f_s}{2}$）分成了N个 frequency bin，目标对应的$f_{peak}$就落在这其中的某个bin中。考虑实信号有镜像频率，如果我们只取正频率部分

$$f_{peak}=\frac{f_s}{N}k，0\le k<\frac{N}{2}$$

从之前的推导很容易看出，$d_{target}$ 与 $f_{peak}$ 成线性关系，即：
$$d_{max}=\frac{c}{2K}{f}_{max}$$

由于在正频率部分，最大的$f_{peak}$即是 $\frac{f_s}{2}$，所以
$$d_{max}=\frac{c}{4K}{f}_s$$

距离分辨率

两个可分辨的 range bin 对应着两个可分辨的 frequency bin，即
$$\Delta d=d_1-d_2=\frac{c}{2K}(f_1-f_2)=\frac{c}{2K}\Delta f=\frac{c}{2K}\frac{f_s}{N}=\frac{c\cdot CRT}{2BW}\frac{f_s}{N}$$

在连续采样的背景下，我们有：
$$\frac{N}{f_s}=CRT$$
于是$\Delta d$进一步可以化简为：
$$\Delta d=\frac{c}{2BW}$$

一个直观的结论是，能达到的距离分辨率只与$BW$，即扫频带宽有关。

无法整周期采样

但在实际上，由于一些装置的设置，往往我们并不会完成整个CRT周期内的采样，即
$$\frac{N}{f_s}=\alpha CPT\le CRT，其中\alpha \le 1$$
于是在这样的情况下，实际得到的距离分辨率并没有预想的那么精细，而要略微粗些。
$$\Delta d=\frac{c}{2BW}\frac{1}{\alpha }\ge \frac{c}{2BW}$$

虽然这里就有聪明的小朋友说了，我可以时域补零啊，那不是看得更仔细了。但遗憾的是“时域补零相当于频域插值”，这改善的只是FFT的是视觉分辨率，而实际上的波长分辨率只由采样数决定（即采样点数M）。假如现在有两个物体落在了同一个原始采样点数换算得到的某个 range bin 中，那么这两个物体在我们最终得到的FFT频谱图中就是无法完成区分的。

我们再对这个分辨率有一个感性的认识，假设扫频带宽为3GHz，则：
$$\Delta d=\frac{c}{2BW}=\frac{3\times 10^8}{2\times 3\times 10^9}m=5mm$$

即一个毫米级的距离分辨率。

CRT的影响

在 TI 关于FMCW雷达的教程视频中，有提出这样一个有趣的问题，即关于 chirp 1 和 chirp 2的讨论，它们具有相同的扫频带宽，但是chirp 1的周期是chirp 2的两倍。

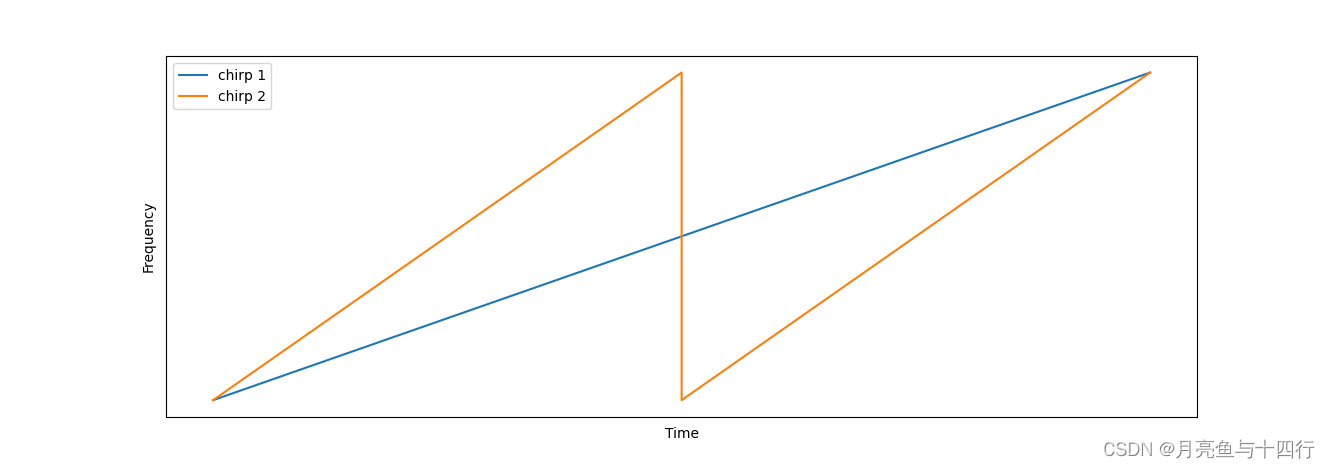
根据之前的推导，我们知道这两个chirp对应的距离分辨率应该是一致的。

但假如我们现在用同一台ADC进行采样：在采样频率相同时，chirp 1能获得的采样点数更多，其对应的波长分辨率也就更高。在采样点数相同的情况下，chirp 1 会比 chirp 2需要的采样率更低，于是对ADC的容忍度提高了；但同时，chirp 1也需要花费更长的时间完成采样。那么，这里呈现的就将是一个对于ADC的 trade-off 。

最后，用一张图总结 range FFT的内容：