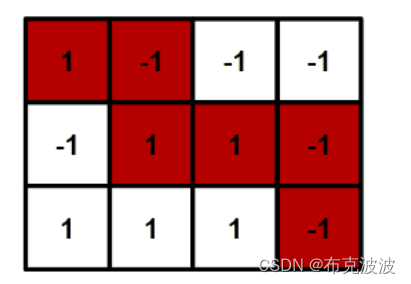
给你一个矩阵，矩阵中每个点是1或者-1，问你是否存在一条路径从左上角到右下角路径上所经过点的总和是0。

类似于数字三角型，dp[i][j]可以用dp[i-1][j]的位置 和 dp[i][j-1]的位置传递过来，我们可以保存每个位置可以达成的和的所有可能性，那么如果当前位置是1，左边一个位置的所有可行的解+1即为当前位置可行的解，当前是-1则左边一个位置的所有可行解-1即为当前位置可行解.两者取并集即可传递。我们可以用bitset来储存当前位置所有可达成路径和（每一个位置代表一种路径和可能，1即为走到当前位置存在该路径和，0则为没有）通过左移右移可以实现低复杂度的转移（除以32）。另外超过正负（n+m-1）/2的路径和不可能产生正确答案，所以我们的bitset开2000即可，超出部分不影响正确答案，也就不用保存。复杂度 O(N*M*2000/32)

ACcode

#include<bits/stdc++.h>
// #define int long long
#define endl '\n'

using namespace std;



typedef pair<int, int> PII;
const int N = 2e5 + 10;

void solve() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>>a(n + 1, vector<int>(m + 1));
    vector<vector<bitset<2010>>>f(n + 2, vector <bitset<2010>>(m + 2));
    for (int i = 1;i <= n;i++)
        for (int j = 1;j <= m;j++)cin >> a[i][j];
    if (a[1][1] == 1)f[1][1][1001] = 1;
    else f[1][1][999] = 1;
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= m;j++) {
            if (a[i][j] == 1) {
                f[i][j] |= (f[i - 1][j] << 1);
                f[i][j] |= (f[i][j - 1] << 1);
            }
            else {
                f[i][j] |= (f[i - 1][j] >> 1);
                f[i][j] |= (f[i][j - 1] >> 1);
            }
        }
    }
    if (f[n][m][1000])cout << "YES" << endl;
    else cout << "NO" << endl;

}

signed main() {
    cin.tie(0)->sync_with_stdio(0);
    cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
        solve();
    return 0;
}