知识目录
- 二次同余方程的解
- 欧拉判别式
- Legendre (勒让德符号)
二次同余方程的解
- 什么是二次同余方程的解
注意这里二次同余方程和一次同余方程是不一样的
在 x 2 x^2 x2 三 a (mod m) 方程中举例 ↓
解即剩余类,因为是模m,所以我们在 [ 0, m-1 ]中逐个代入看是否满足方程式。 - 解的说法有三种:
①平方剩余
②平方非剩余
要满足这两种情况的条件:(a,m)= 1,首先要互素,其次再代入完全剩余系看有没有解
③既不是平方剩余也不是平方非剩余
这种情况是在(a,m) 不是互素的情况下,即使是有解,也不是平方剩余和平方非剩余 - 只需要代入一半的完全剩余系的数字
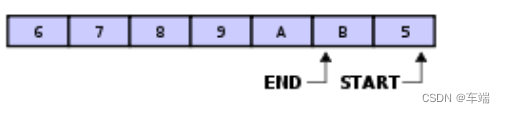
如下图所示,因为 x 2 x^2 x2在模的世界里,m-x与x是差一个正负符号而已,在二次方程式中正好解决了该问题,那么就可以利用该特性,只需要在完全剩余系中找解的时候,
代入一半即可[0,m/2 ] or [ m/2, m],代入哪一半都行,这两部分代入后结果是一样的。
解释:将下图的m-x平方展开后就明白为什么只需要代入一半(记住:是要模m的)

欧拉判别式
上面讲述了二次同余方程的解是从何而来,如何找解。那么欧拉判别式就是用来判断一个解是否是二次同余方程式的平方剩余或者平方非剩余
- 使用欧拉判别式的条件
方程式: x 2 x^2 x2 三 a (mod p)
1:p必须是奇素数(奇素数,不包括2)
2:(a, p) = 1,ap必须互素
(很显然必须要互素,因为本身判断的就是平方剩余/非剩余的关系,开头已经讲清楚了)
满足以上条件则:
若 a a a ( ^( ( p ^p p − ^- − 1 ^1 1 ) ^) ) / ^/ / 2 ^2 2 三 1 (mod p),则a是平方剩余。
若 a a a ( ^( ( p ^p p − ^- − 1 ^1 1 ) ^) ) / ^/ / 2 ^2 2 三 -1 (mod p),则a是平方非剩余。

Legendre (勒让德符号)
设p为奇素数,(a, p)= 1,则 ↓
若:(
a
p
\frac{a}{p}
pa) = 1 ,则a为平方剩余
若:(
a
p
\frac{a}{p}
pa) = -1 ,则a为平方非剩余
(
a
p
\frac{a}{p}
pa)就叫做a对p的勒让德符号
其实就是用了上面的欧拉判别式↓↓
a
a
a
(
^(
(
p
^p
p
−
^-
−
1
^1
1
)
^)
)
/
^/
/
2
^2
2 三 1 (mod p)
a
a
a
(
^(
(
p
^p
p
−
^-
−
1
^1
1
)
^)
)
/
^/
/
2
^2
2 三 -1 (mod p)
下面围绕勒让德符号展开一些推论和定理:
- ( 1 p \frac{1}{p} p1) = 1 (证明可以使用欧拉判别式,1的多少次方终究还是1)
- ( − 1 p \frac{-1}{p} p−1) = ( − 1 ) p − 1 2 (-1)^\frac{p-1}{2} (−1)2p−1 (本条推论就是欧拉判别式)
- ( 2 p \frac{2}{p} p2) = ( − 1 ) p 2 − 1 8 (-1)^\frac{p^2-1}{8} (−1)8p2−1
勒让德符号中可以像分子那样拆开,没有限制条件。