文章目录
- 1.为什么hashmap用红黑树不用二叉树和平衡二叉树
- 1.1 二叉树(Binary Search Tree)
- 1.2 红黑树(Red Black Tree)
- 1.3 平衡二叉树(Balence Binary Tree)也称AVT
- 2.为什么mysql用b+数,不用B数或B*数作为存储引擎的数据结构?
- 2.1 B树
- 2.2 B+树
- 2.3.B*树
- 2.4.R树
- 2.5.树的演进
- 3.深入红黑树
- 3.1 旋转方式(4种)
- 3.1.1 节点左旋(节点下右侧子节点深度过长)
- 3.1.2 节点右旋(节点下的子节点左侧深度过长)
- 3.2 红黑树自平衡原则(何时触发左右旋及变色)重点
- 3.2.1.变色
- 3.2.2.左旋
- 3.2.3.右旋
- 3.2.4例子
- 3.2 插入自平衡(最多2次旋转)
- 3.3 删除自平衡(最多3次旋转)
1.为什么hashmap用红黑树不用二叉树和平衡二叉树
1.1 二叉树(Binary Search Tree)
特性:
1.每个节点最多有两颗子树,所以二叉树中不存在度大于2的节点;(度=子节点个数)
2.左子树和右子树是有序的,不能任意颠倒
3.即使一个节点只有一颗子树,也要区分是左子树还是右子树
缺点:极端情况下退化成链表,导致索引效率大大降低,也间接影响了删除性能。
1.2 红黑树(Red Black Tree)
红黑树的出现就是为了 解决二叉树退化成链表的问题;它是趋于平衡的树
1.3 平衡二叉树(Balence Binary Tree)也称AVT
特性
1.根节点左边的节点值必须小于根节点,根节点右边的节点值必须大于根节点;
2.每个节点的左右深度差值不能大于1;
缺点:由于节点深度差值不能大于1,所以在大量插入或删除的时候,会一直调整数的平衡,此时性能不如红黑树;原因是由于红黑树的可以容忍最大深度不能超过最小深度2倍,大量的插入和删除时,性能优于AVT。
2.为什么mysql用b+数,不用B数或B*数作为存储引擎的数据结构?
2.1 B树
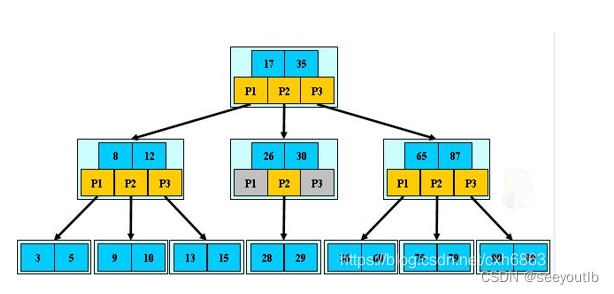
特点:
1.每个节点都存储key和value,所有节点组成这棵树,并且叶子节点的指针为null
2.任何一个关键字只出现在一个节点中;如key
3.搜索有可能在非叶子节点结束
4.在关键字全集做一次查找,性能逼近二分查找
2.2 B+树
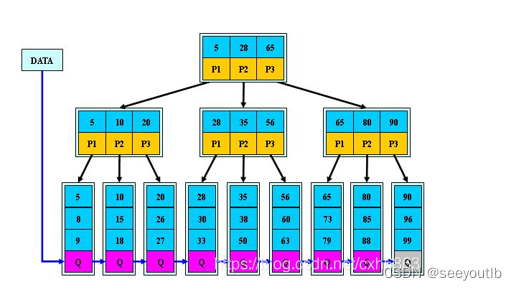
特点:
1.只有叶子节点存储数据,包含这颗数的所有索引值,叶子节点不存储指针
(非叶子节点只存储索引值,不存储实际的数据,并非真正的data)
2.增加了访问数据的指针,每个叶子节点增加一个指向相邻叶子节点的指针(范围查下性能大幅提升)
2.3.B*树
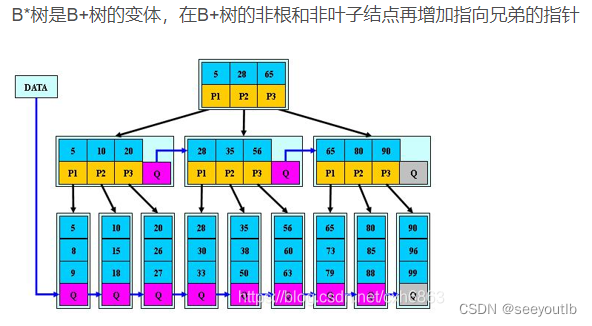
特点:B*树是对B+树的改进,在非叶子节点的兄弟之间增加了双向指针,目的优化B+数在叶子节点满而分裂时的效率;
构建过程对比:
B+树,在叶子节点数据满时,叶子就会分裂;
B*树,在叶子节点数据满时,会询问兄弟节点空间是否满,如果没满,则转移部分关键字;如果满了则每个兄弟节点拿出1/3数据创建新的节点
2.4.R树
R树特性:叶子节点会组多维空间层,查询时性能大幅降低,不再适合数据场景
2.5.树的演进
1、首先,为了保证树的节点均匀分布,所以在二叉树的基础上加上了平衡算法,就有了平衡二叉树。
2、为了减少树的高度,所以B树一个节点下面可以添加N个子节点,然后每个节点的大小限制在磁盘块容量大小,让节点只需要通过一次IO就能读取到所有数据,通过增加节点存储的数据减少了树的高度,而节点的数据变多并没有让IO次数变多。
3、B+树在B树的基础上,在查询的稳定性 和排序方面进行了优化,因为B+树所有的数据都会保存到叶子节点,然后所有叶子节点本身是有序的。
4、B*树为了减少 树在构建过程中节点的拆分、合并次数,所以在每个节点上都保存了旁边节点的指针,在节点需要进行拆分、合并时,优先从旁边节点挪数据,从而减少构建过程中节点拆分、合并的次数,提升了树的构建性能。
3.深入红黑树
优化:解决二叉树极端情况下退化成链表大大降低索引效率的问题
3.1 旋转方式(4种)
3.1.1 节点左旋(节点下右侧子节点深度过长)
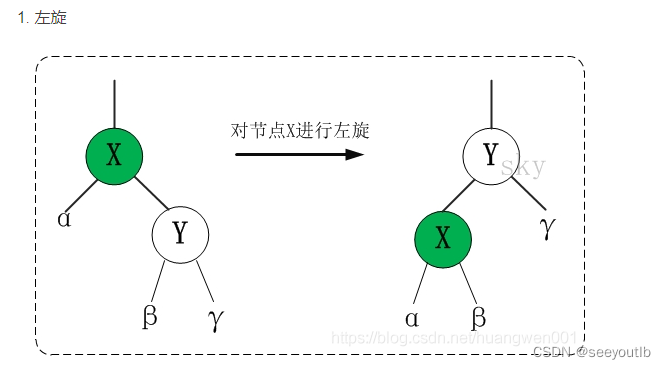
角色:
- 轴节点(旋转节点): X
- 被旋节点:Y
- 子节点:α(阿尔法)、β(贝塔)、γ(伽马)
左旋原理:
1.轴节点右侧子节点作为轴节点的父节点
2.原轴节点的左侧节点父节点和位置不变
3.原被旋节点右侧节点父节点和位置不变
4.轴节点右侧子节点的左侧子节点作为轴节点的右侧子节点
3.1.2 节点右旋(节点下的子节点左侧深度过长)
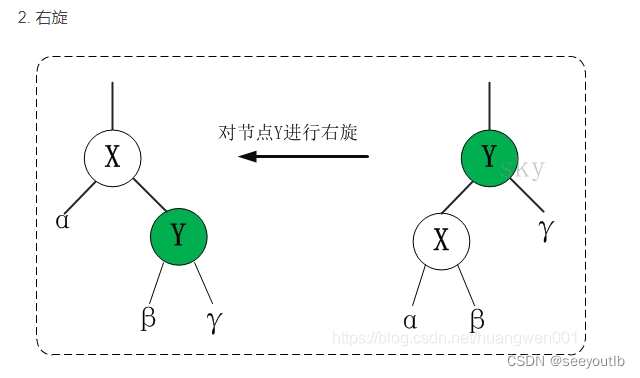
角色:
- 轴节点(旋转节点): Y
- 被旋节点:X
- 子节点:α(阿尔法)、β(贝塔)、γ(伽马)
右旋原理
1.轴节点的左侧子节点作为轴节点的父节点
2.轴节点右侧子节点父节点和位置不变
3.被旋节点左节点的父节点和位置不变
4.轴节点的左侧子节点作为被旋节点的右节点
左右旋小结:轴节点左子节点和被旋节点右子节点的父节点和位置不变
位置不变指的是:子节点旋转前和旋转后依然是父节点的左子节点或右子节点;如上图α和γ节点
3.2 红黑树自平衡原则(何时触发左右旋及变色)重点
旋转和变色规则:所有插入节点默认为红色
3.2.1.变色
条件:插入节点的父节点和叔叔节点为红色
步骤:
1.父节点和叔节点变为黑色
2.把祖父节点变为红色
3.把祖父节点作为插入节点
另外变色条件:红黑树为空时,插入当前节点,将当前节点变为黑色
3.2.2.左旋
条件:当前父节点为红色,叔叔为黑色,且当前节点为右子树
步骤:以父节点作为轴节点左旋
3.2.3.右旋
条件:当前父节点为红色,叔叔为黑色,且当前节点为左子树
步骤:
1.把父节点变为黑色
2.把祖父节点变为红色
3.以祖父节点右旋
3.2.4例子
1.插入节点62:
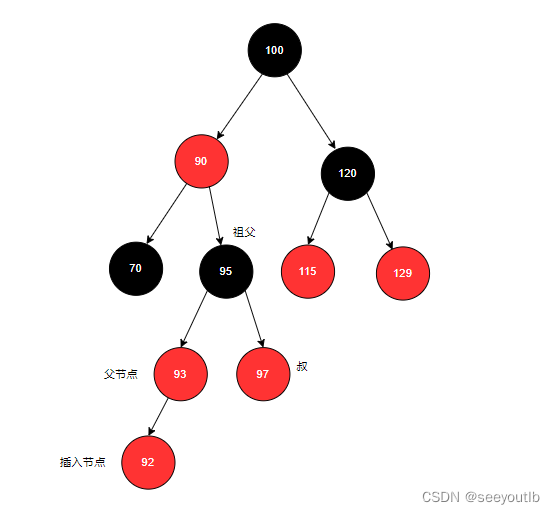
2.满足变色条件,进行变色。变色后如下
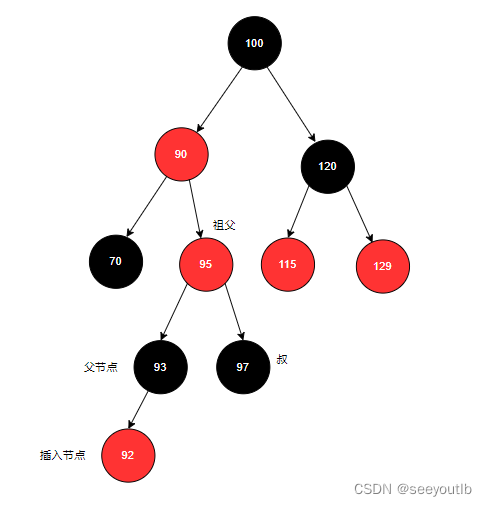
再将祖父节点作为插入节点,如下图:
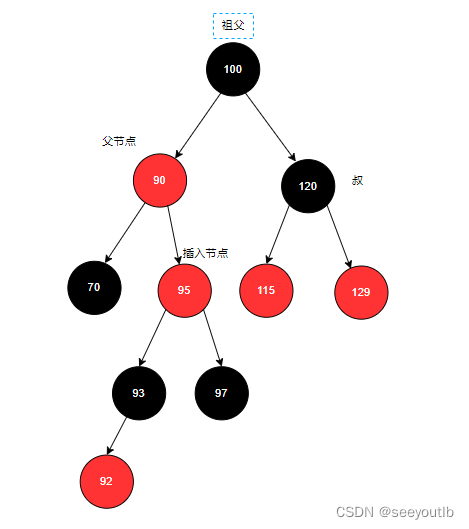
3.满足左旋条件:旋转后如下
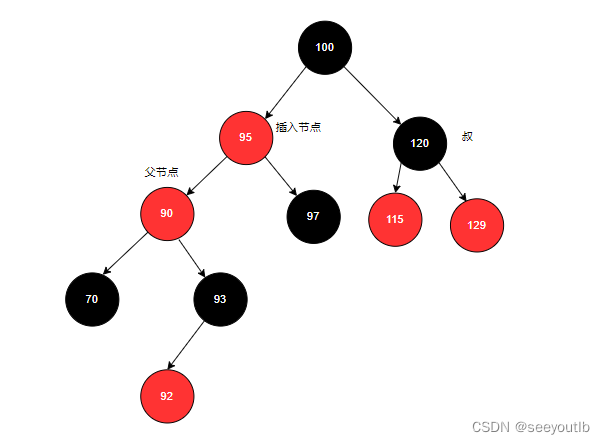
4.再以90作为插入节点,再次判断是否要变色或旋转
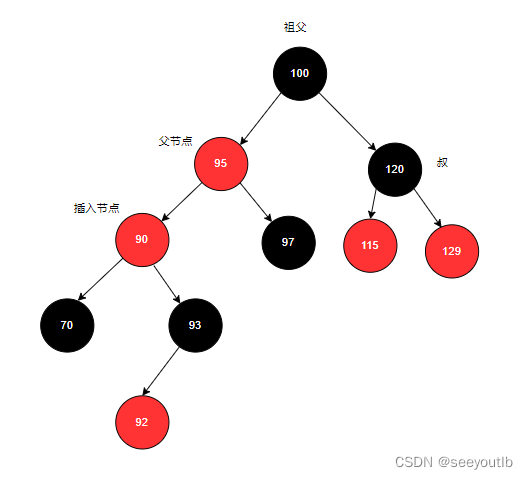
5.满足右旋条件:先变色,后旋转
先变色:变色后
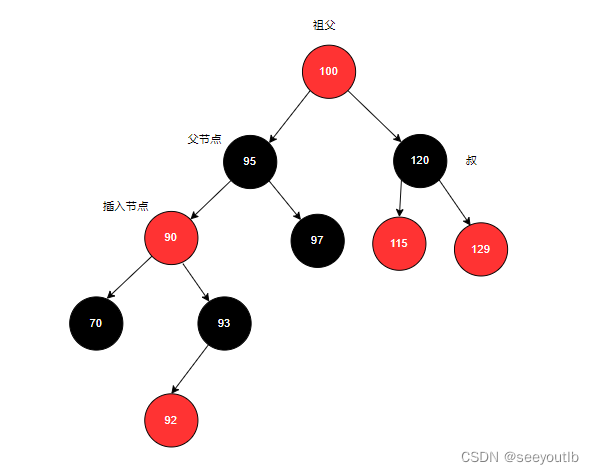
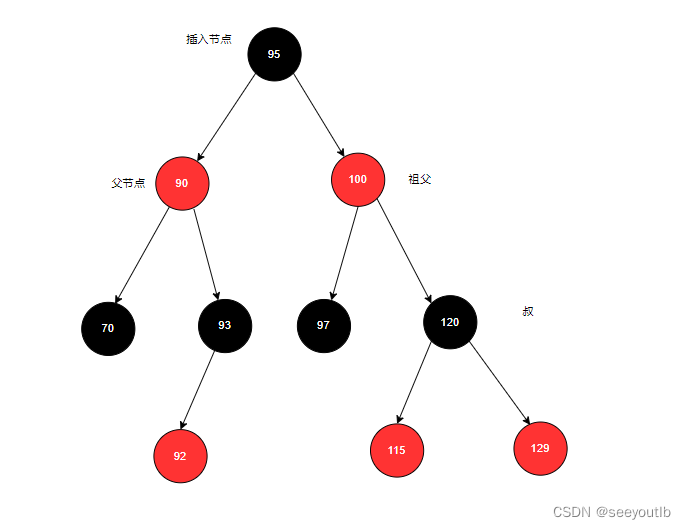
以祖父作为插入节点右旋:旋转后
3.2 插入自平衡(最多2次旋转)
1.插入时,红黑树为空,插入节点变为黑色
2.插入时,父节点为黑色,直接插入
3.当父节点为红色时,情况有5种,惨遭上述变色左右旋规则循环直到满足红黑树性质
详情请看java-TreeMap或HashMap源码
java红黑树hashmp插入分析:
3.3 删除自平衡(最多3次旋转)
详情请看java-TreeMap或HashMap源码
![buu [NPUCTF2020]这是什么觅 1](https://img-blog.csdnimg.cn/dfc1504fa71c49ef89878dbd9de4176c.png)



![[YOLO] yolov4 博客笔记](https://img-blog.csdnimg.cn/4fc6b9403e9f495f94d896cc4bf3beba.png)