前言

此专栏包含408考研数据结构全部内容，除其中使用到C++引用外，全为C语言代码。使用C++引用主要是为了简化指针的使用，避免二重指针的出现。

已完成内容

[数据结构]：01-顺序表（C语言实现）_Chandni.的博客-CSDN博客

[数据结构]：02-单链表（C语言实现）_Chandni.的博客-CSDN博客

[数据结构]：03-栈（C语言实现）_Chandni.的博客-CSDN博客

[数据结构]：04-循环队列（数组）（C语言实现）_Chandni.的博客-CSDN博客

[数据结构]：05-循环队列（链表）（C语言实现）_Chandni.的博客-CSDN博客

[数据结构]：06-队列（链表带头结点）（C语言实现）_Chandni.的博客-CSDN博客

[数据结构]：07-二叉树（无头结点）（C语言实现）_Chandni.的博客-CSDN博客

[数据结构]：08-顺序查找（顺序表指针实现形式）（C语言实现）_Chandni.的博客-CSDN博客

[数据结构]：09-二分查找（顺序表指针实现形式）（C语言实现）_Chandni.的博客-CSDN博客

二叉排序树实现

01-开发环境

语言：C/C++14

编译器：MinGW64

集成开发环境：CLion2022.1.3

02-文件布局

请在CLion集成开发环境中创建C++可执行程序，否则无法运行，原因上面已解释。

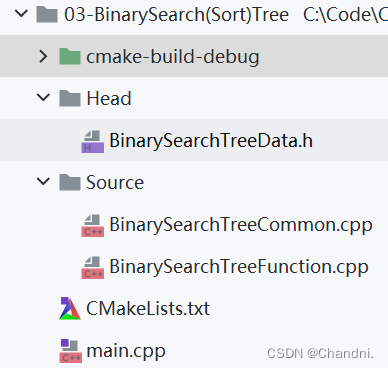
03-代码

01-主函数

用于测试二叉排序树的创建、查找、删除。

其中创建、查找使用了两种方式实现。一种是非递归形式（for循环），另一种是递归形式。

#include "./Head/BinarySearchTreeData.h"
#include "./Source/BinarySearchTreeCommon.cpp"
#include "./Source/BinarySearchTreeFunction.cpp"

int main() {
    // 创建
    BinaryTree BST = NULL;
    int data[7] = {54, 20, 66, 40, 28, 79, 58};
    int Length = 7;
    BinarySearchTreeCreate(BST, data, Length);
    InOrderTraversalTree(BST); // 有小到大
    printf("\n");

    // 查找
    BinaryTree OutputTree;
    OutputTree = BinarySearchTreeSearch(BST, 66);
    if (OutputTree) {
        printf("Value = %d\n", OutputTree->data);
    } else {
        printf("Not Find.\n");
    }

    // 递归创建
    BinaryTree BST1 = NULL;
    BinarySearchTreeRecursionCreate(BST1, data, Length);
    InOrderTraversalTree(BST1); // 有小到大
    printf("\n");

    // 查找
    OutputTree = BinarySearchTreeRecursionSearch(BST1, 66);
    if (OutputTree) {
        printf("Value = %d\n", OutputTree->data);
    } else {
        printf("Not Find.\n");
    }

    // 删除
    BinarySearchTreeRecursionDelete(BST, 66);
    InOrderTraversalTree(BST);
    printf("\n");
    return 0;
}

02-头文件

用于存储结构体和常量等。

//
// Created by 24955 on 2023-03-04.
//

#ifndef INC_03_BINARYSEARCH_SORT_TREE_BINARYSEARCHTREEDATA_H
#define INC_03_BINARYSEARCH_SORT_TREE_BINARYSEARCHTREEDATA_H
// 头文件
#include <stdio.h>
#include <stdlib.h>

// 常量
typedef int ElemType;

// 结构体
typedef struct BinaryTreeNode {
    ElemType data;
    struct BinaryTreeNode *lChild, *rChild;
} BinaryTreeNode, *BinaryTree;
#endif //INC_03_BINARYSEARCH_SORT_TREE_BINARYSEARCHTREEDATA_H

03-BinarySearchTreeCommon.cpp

用于存储二叉排序树打印函数（中序遍历--为有序排列，从小到大）。

//
// Created by 24955 on 2023-03-04.
//
// 中序遍历
void InOrderTraversalTree(BinaryTree BTree) {
    /*
     * 1. 左、自身、右*/
    if (BTree != NULL) {
        InOrderTraversalTree(BTree->lChild);
        printf("%3d", BTree->data);
        InOrderTraversalTree(BTree->rChild);
    }
}

04-BinarySearchTreeFunction.cpp

用于存储二叉排序树创建、查找、删除等函数。

//
// Created by 24955 on 2023-03-04.
//
// 二叉排序树插入结点
void BinarySearchTreeInsert(BinaryTree &BST, ElemType value) {
    /*
     * 1. 初始化新结点
     * 2. 判断是否为根节点
     * 3. 不为根节点比较两节点数值大小决定插入位置*/
    // 初始化新结点
    BinaryTree NewNode = (BinaryTree) calloc(1, sizeof(BinaryTreeNode));
    NewNode->data = value;
    // 循环树结点标签
    BinaryTree BSTLabel = BST;
    if (BST == NULL) {
        BST = NewNode;
    } else {
        // 插入结点
        while (BSTLabel) {
            if (BSTLabel->data > value) {
                if (BSTLabel->lChild == NULL) {
                    BSTLabel->lChild = NewNode;
                    break;
                } else {
                    BSTLabel = BSTLabel->lChild;
                }
            } else {
                if (BSTLabel->rChild == NULL) {
                    BSTLabel->rChild = NewNode;
                    break;
                } else {
                    BSTLabel = BSTLabel->rChild;
                }
            }
        }
        // 或者采用以下代码(用空间减少循环中判断，即换时间)
        /*
         BinaryTree BSTLabelParent;
         while (BSTLabel) {
            BSTLabelParent = BSTLabel;
            if (BSTLabel->data > value) {
                BSTLabel = BSTLabel->lChild;
            } else { // 不用考虑相等情况，408中未考过存在相同值的情况
                BSTLabel = BSTLabel->rChild;
            }
         }
         if (BSTLabelParent->data > value){
            BSTLabelParent->lChild = NewNode;
         } else {
            BSTLabelParent->rChild = NewNode;
         }
         */
    }
}

// 创建二叉排序树
void BinarySearchTreeCreate(BinaryTree &BST, const ElemType data[], int Length) {
    /*
     * 1. 初始化树根
     * 2. 按数据值大小插入树*/
    // const是C语言的一种关键字，它所限定的变量是不允许被改变的
    // 树根
    BST = NULL;
    for (int i = 0; i < Length; i++) {
        BinarySearchTreeInsert(BST, data[i]);
    }
}

// 二叉排序树查找(也可以采用递归方式)
BinaryTree BinarySearchTreeSearch(BinaryTree BST, ElemType value) {
    /*
     * 1. 判断根节点值是否与待查找值相等
     * 2. 若相等返回根结点地址
     * 3. 若不相等判断是否大于当前结点值若小于BST = BST->lChild;反之大于BST = BST->rChild;
     * 4. 若未查到返回NULL*/
    while (BST) {
        if (BST->data == value) {
            return BST;
        } else if (BST->data > value) {
            BST = BST->lChild;
        } else {
            BST = BST->rChild;
        }
    }
    return NULL;
}

/*************************** 以下为递归方式实现 *******************************/
// 递归方法插入树新结点
void BinarySearchTreeRecursionInsert(BinaryTree &BST, ElemType value) {
    /*
     * 1. 判断当前结点是否为空
     * 2. 若为空插入
     * 3. 若不为空判断大小，进行递归*/
    if (BST == NULL) {
        // 初始化新结点
        BinaryTree NewNode = (BinaryTree) calloc(1, sizeof(BinaryTreeNode));
        NewNode->data = value;
        BST = NewNode;
    } else {
        if (BST->data > value) {
            BinarySearchTreeRecursionInsert(BST->lChild, value);
        } else {
            BinarySearchTreeRecursionInsert(BST->rChild, value);
        }
    }
}

// 调用递归插入函数创建二叉排序树
void BinarySearchTreeRecursionCreate(BinaryTree &BST, const ElemType data[], int Length) {
    /*
     * 1. 初始化树根
     * 2. 按数据值大小插入树*/
    // const是C语言的一种关键字，它所限定的变量是不允许被改变的
    // 树根
    BST = NULL;
    for (int i = 0; i < Length; i++) {
        BinarySearchTreeRecursionInsert(BST, data[i]);
    }
}

void BinarySearchTreeRecursionDelete(BinaryTree &BST, ElemType value) {
    /*
     * 1. 若删除元素值比当前元素值小，递归传入左孩子
     * 2. 若删除元素值比当前元素值大，递归传入右孩子
     * 3. 若相等，则判断当前元素左、右孩子是否为空
     * 4. 若其中任意一个为空，则将另一个替代要当前元素(要删除元素)
     * 5. 若都不为空，循环寻找当前元素左子树中最大值，替代当前元素值，并删除左子树中用于替代的结点*/
    // 防止输入的为树中未包含元素，无法停止递归
    if (BST == NULL) {
        return;
    }
    if (BST->data > value) {
        BinarySearchTreeRecursionDelete(BST->lChild, value);
    } else if (BST->data < value) {
        BinarySearchTreeRecursionDelete(BST->rChild, value);
    } else {
        BinaryTree FreeNode;
        // 若左、右孩子其中任意一个为空，则将另一个替代要当前元素(要删除元素)
        if (BST->lChild == NULL) {
            FreeNode = BST;
            BST = BST->rChild;
            free(FreeNode);
        } else if (BST->rChild == NULL) {
            FreeNode = BST;
            BST = BST->lChild;
            free(FreeNode);
        } else {
            // 左、右孩子都不为空
            // 一般删除策略为：左子树的最大数据 或 右子树的最小数据，替代要删除的结点
            // 此处采用左子树的最大数据
            BinaryTree TemporaryTree = BST->lChild;
            // 寻找左子树中的最大值
            while (TemporaryTree->rChild) {
                TemporaryTree = TemporaryTree->rChild;
            }
            // 替代，删除替代结点
            BST->data = TemporaryTree->data;
            // 此处注意不要传入TemporaryTree
            // 经单点调试发现，传入TemporaryTree会造成乱码(未将叶子结点设为NULL)
            BinarySearchTreeRecursionDelete(BST->lChild, TemporaryTree->data);
        }
    }
}

// 二叉排序树查找-递归方式
BinaryTree BinarySearchTreeRecursionSearch(BinaryTree BST, ElemType value) {
    /*
     * 1. 返回值为NULL或所查找到的结点*/
    if (BST != NULL && BST->data != value) {
        if (BST->data > value) {
            BST = BinarySearchTreeRecursionSearch(BST->lChild, value);
        } else {
            BST = BinarySearchTreeRecursionSearch(BST->rChild, value);
        }
    }
    return BST;
}