百度“松果“ OJ赛第一周 题解

news2025/1/16 9:03:07

百度"松果" OJ赛第一周 题解

第一周的周赛基本考察的都是模拟和递推递归问题，虽然不涉及很难的算法，但是还是比较考察代码能力和思维能力的。

1.数据流的中位数

题意：要求你做一个系统可以进行两个操作，第一个操作是向系统中存入一个数，第二个操作是返回当前系统中数的中位数。
思路：由于这个过程是动态进行的，所以我们如果每次都加入一个数再进行排序，时间复杂度 O ( n 2 l o g n ) O(n^2logn) O(n2logn)，无疑会超时。那么我们就需要想办法维护好中位数，考虑到是中位数，那么我们就可以把所有的数分成左右两部分进行维护。考虑到添加元素后需保持单调性，我们可以用堆来解决这个问题。手写堆较麻烦，这里就使用STL中的优先队列(priority_queue)来进行操作。
优先队列简单介绍：

#include<queue>//使用时需要加上这个头文件或者用万能头
priority_queue<int> q;//大根堆
priority_queue<int,vector<int>,greater<int> > q;//小根堆

对于维护中位数，我们可以用一个大根堆来存左边的数。（堆顶存的就是左边最大值），用一个小根堆来存右边的数。（堆顶存的就是右边的最小值）。这样如果两个堆的大小相同，那么中位数，就是两个堆顶数之和的平均值，否则，中位数就是堆的大小较大的堆顶值。
接着我们考虑添加数的操作：
第一个数直接添加到左边的堆中，接下来数的插入分为以下几种情况：
第一种两个堆的大小相同，那么我们就需要考虑插入到哪一个堆中，我们只需要去比较插入值x和左边堆的堆顶去比较即可。如果x<左边的堆顶，那么就直接插入到左边，反之插入到右边的堆中。(只有这样才能维护好中位数，即保证左边堆的最大值小于等于右边堆的最小值)。
第二种左边堆的元素比右边堆的元素多，这种情况我们就需要将值x插入到右边的堆中了，但是可以直接将x插入到右边的堆中吗？
显然是不可以的。比如如果插入值x小于左边堆的堆顶。那么如果我们直接将x插入到右边的堆中，那么是不是就不满足上面括号中的条件了。自然中位数的维护就出现了问题，所以对于这种情况，我们需要进行一个 替换，将左边堆顶的元素插入到右边堆中，然后将左边堆顶元素从左边堆中去除，再将x插入到左边的堆中，这样既可以保证操作后两边堆大小一致，且符合条件。对于x大于左边堆顶的情况，就直接插入到右边堆中就可以了。
第三种情况和上面情况类似，按照相同方式分情况处理即可。
代码：

#include<bits/stdc++.h>

using namespace std;

#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\n'

typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;


void Showball() {
    LL n;
    cin>>n;
    priority_queue<LL> lq;//左边的堆，大根堆
    priority_queue<LL,vector<LL>,greater<LL>> rq;
    //右边的堆，小根堆
    while(n--){
        char op;
        LL x;
        cin>>op;
        if(op=='+') {//添加数操作
            cin>>x;
            if(lq.empty()) lq.push(x);//第一个数的插入
            else if(lq.size()==rq.size()) {//两堆大小相同
              if(x<lq.top()) lq.push(x);
              else rq.push(x);
            }
            else if(lq.size()>rq.size()){//左堆元素更多
               //x大于左堆顶，直接插入右堆
              if(x>lq.top()) rq.push(x);
              /*否则，需要将左堆堆顶加入右堆，
              并且去除，再将x插入左堆*/
              else{
                rq.push(lq.top());
                lq.pop();
                lq.push(x);
              }
            }
            else {//右堆元素数大于左端的情况
              if(x<rq.top()) lq.push(x);
              else{
                lq.push(rq.top());
                rq.pop();
                rq.push(x);
              }
            }
        }else{//输出中位数
            if(lq.size()==rq.size()) 
            cout<<(LL)(lq.top()+rq.top())/2.0<<endl;
            else if(lq.size()>rq.size()) 
            cout<<lq.top()<<endl;
            else cout<<rq.top()<<endl;
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T = 1;
    //cin>>T;
    while(T--)
        Showball();
    return 0;
}

2.碰碰车

题意：给你n个碰碰车的初始坐标和方向(1表示向右，-1表示向左)。当两个碰碰车相撞时，会立即掉头(忽略碰撞时间)，输出t秒后，每辆碰碰车的位置和方向(1表示向右，-1表示向左,0表示两车相遇)。
思路：一开始拿到这题也是感觉很绕的，这时候我们就需要画图分析样例是怎么得到的。
输入：
5 2
4 1
5 -1
7 1
2 1
6 -1
输出：
4 0
4 0
9 1
3 -1
6 1
t=0时：
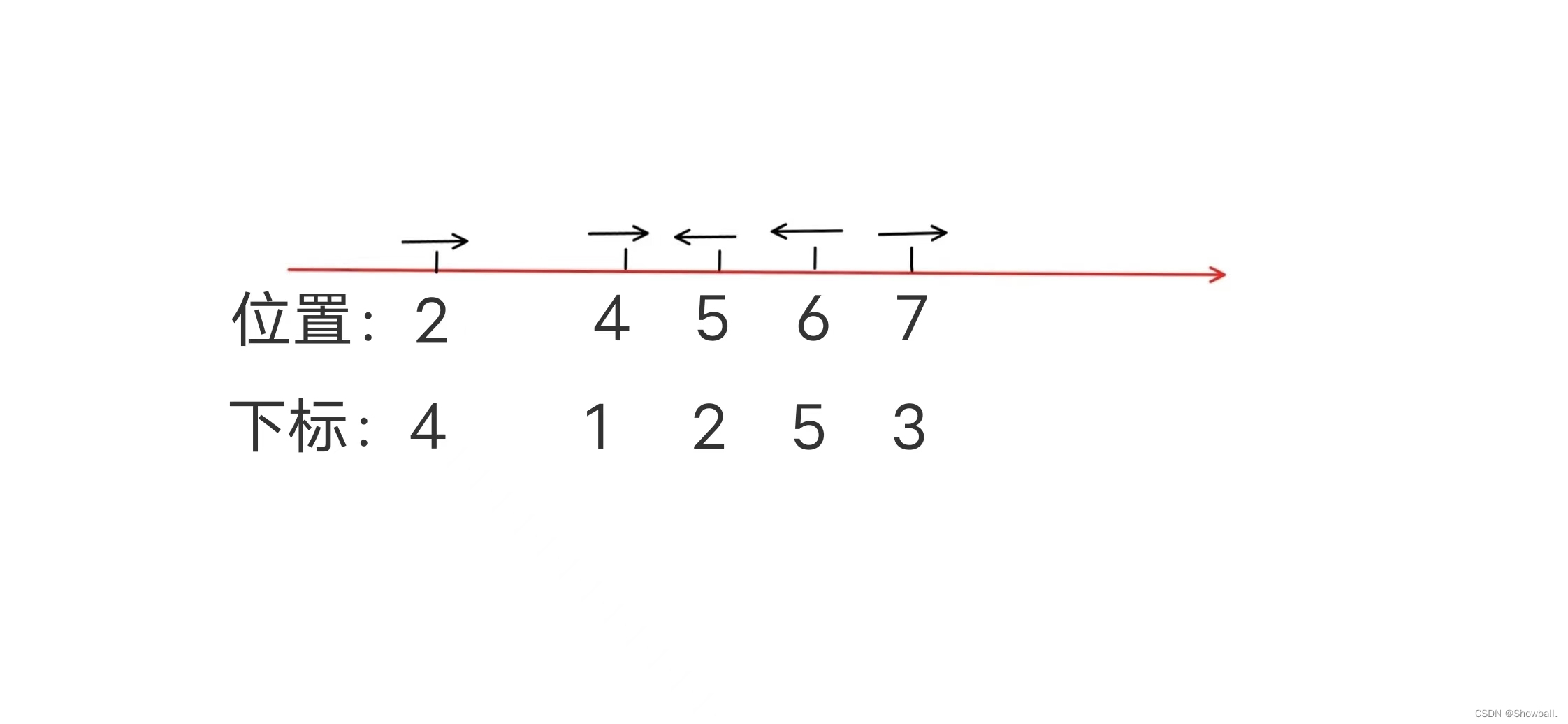
在这里插入图片描述

t=1时：
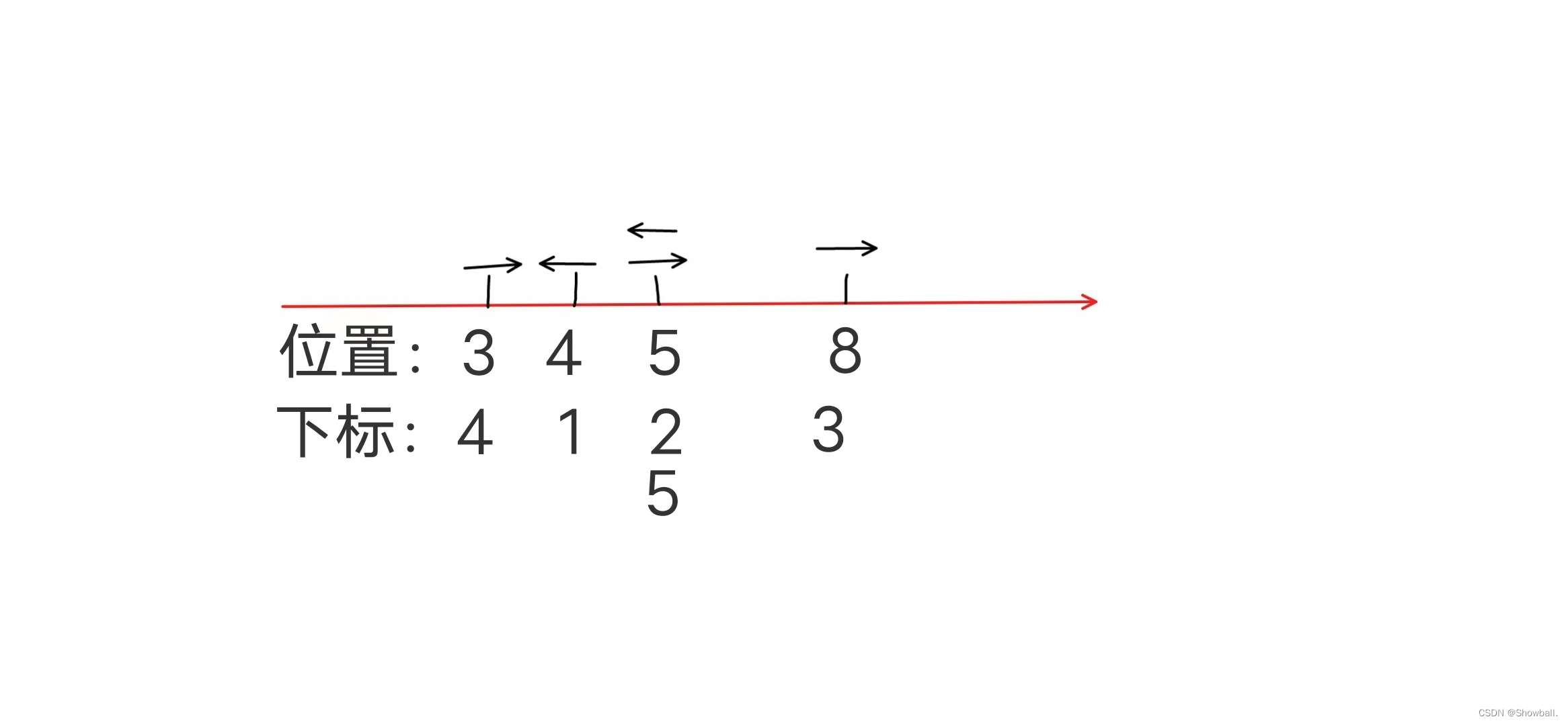
在这里插入图片描述

t=2时：
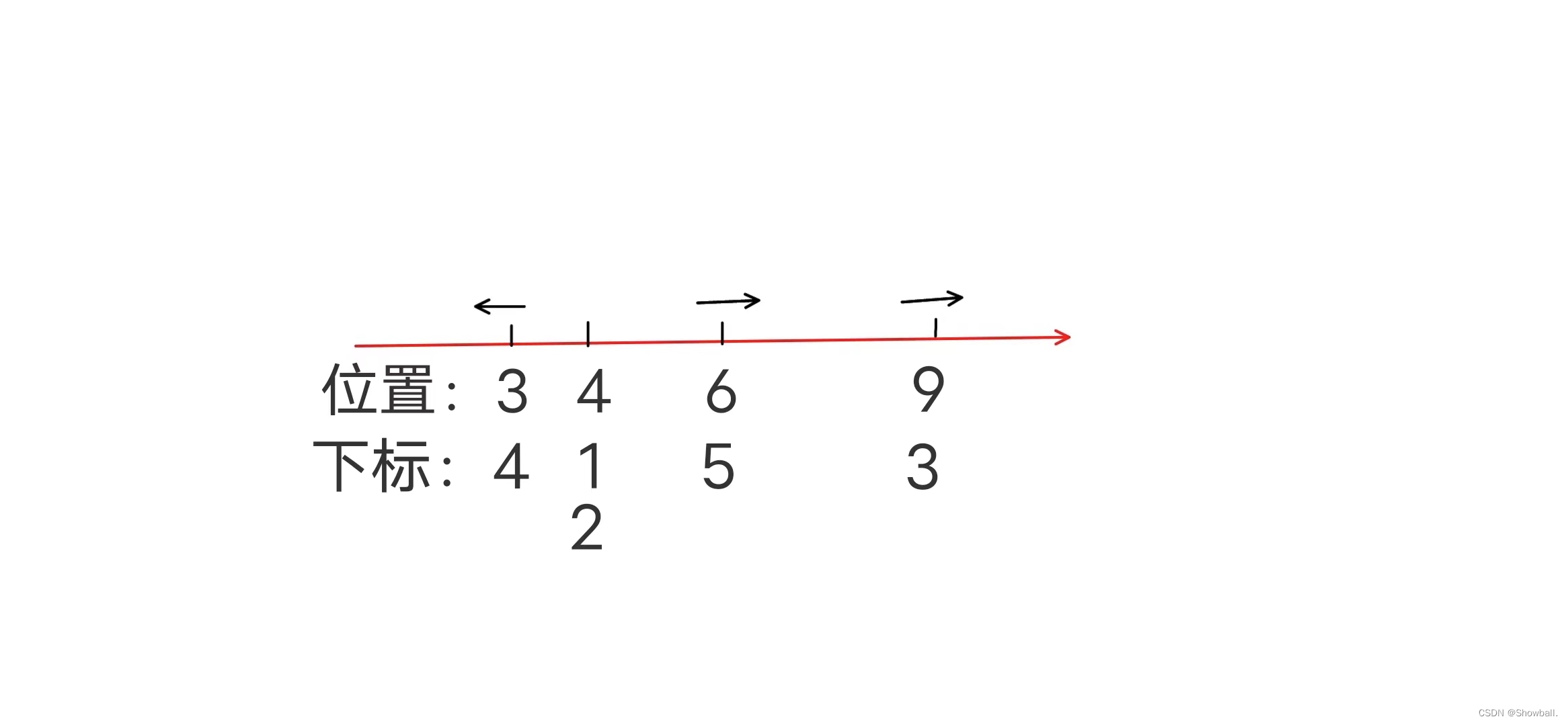
在这里插入图片描述
通过以上模拟样例的过程我们可以发现：
如果两个碰碰车相向而行，并且距离1，那么他们会用0.5s相撞，然后换方向后再走0.5s。相当于位置不变，方向改变。
如果两个碰碰车相向而行，并且距离2，那么他们会用1s相撞，然后换方向。
如果对于这两种情况直接进行模拟，我们难以去模拟相撞不同的情况，所以这里需要进行一点点转变，我们将所有点的初始坐标全部扩大2倍，那么原来相向而行距离1就会变成距离2，距离2会变成距离4。这样我们就可以模拟一秒一秒的进行模拟，但是如果知识距离扩大2倍，那么原来的关系也不会成立，所以总时间也需要扩大二倍。
这样处理后我们发现问题会被简化，因为1秒后如果两车相撞，他们的位置一定是相同的，因为我们把距离扩大了2倍，原来0.5s相撞的现在会1秒后相撞。这样我们就可以每次模拟每秒后每个车的位置，然后判断如果一个位置出现了两辆车以上，那么就说明相撞了，那么我们就需要将这些车辆的方向进行改变。这里我们可以用map来存一下每个位置出现的次数。
一共t秒，每次我们都要枚举一遍n个车辆，所以时间复杂度 O ( t n ) O(tn) O(tn)。因为t和n都是1000的范围，这个复杂度是可以通过的。
代码：

#include<bits/stdc++.h>

using namespace std;

#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\n'

typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;


void Showball() {
  int n,t;
  cin>>n>>t;
  t*=2;//时间扩大2倍
  map<int,int> mp;//用来存每个位置当前有多少辆车
  vector<int> a(n),v(n);
  for(int i=0;i<n;i++){
    cin>>a[i]>>v[i];
    a[i]*=2;//位置扩大2倍
    mp[a[i]]++;
  }
  while(t--){
    for(int i=0;i<n;i++){
      mp[a[i]]--;/*因为这辆车要去下一个位置，
      所以当前位置车辆减1.*/
      a[i]+=v[i];
      mp[a[i]]++;//到达位置的车辆数+1
    }

    for(int i=0;i<n;i++){
       //如果当前车辆数大于1，那么相撞了，方向改变
      if(mp[a[i]]>1) v[i]*=-1;
    }
  }
  for(int i=0;i<n;i++){
    //因为我们扩大了2倍位置，所以输出时需要还原。
    //注意如果某个位置车的数量大于1那么方向需要输出0
    cout<<a[i]/2<<" "<<v[i]*(mp[a[i]]==1)<<endl;
  }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T = 1;
    //cin>>T;
    while(T--)
        Showball();
    return 0;
}

3. 移水造海

题意：给你一个宽度为n，每一列高为 h i h_i hi​的土地。
你有一个无限水桶，每次你可以选择一列土地(不能选两边),往该列土地到一桶水，一桶水，可以填一个高度单位的土地，如果倒水量高于该列土地的左边或者右边，那么水就会溢出，相当于没有到过，问你至少需要多少桶水，可以使得，这片土地变成海(即在任何位置到水都会溢出)。
思路：这题画一个图就可以分析出规律，我们接着按照样例作图。
样例：
9
4 1 2 3 6 3 2 1 3
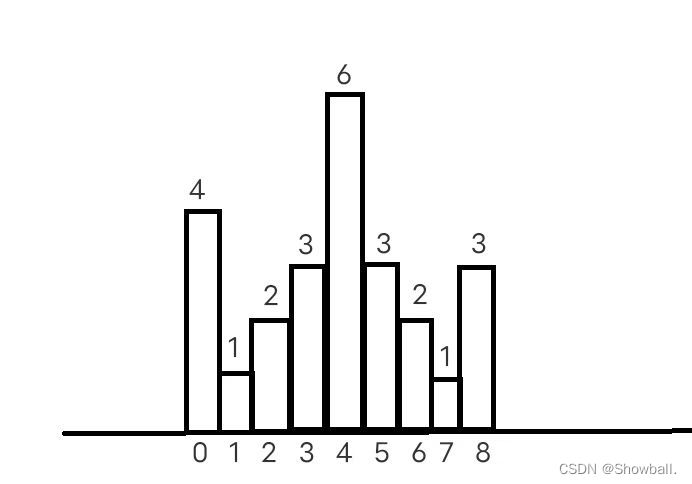
在这里插入图片描述
我们观察这个图，可以发现对于1-7列土地，我们每列最多可以到入的水数量是由左边最高土地和右边最高土地的较小值来约束的。
比如1号土地，可以倒入的水的数量就是左边最大值4和右边最大值6取一个最小值与该土地高度的差值，即3桶，依次算一下剩下的土地。分别是：3, 2 , 1, 0, 0, 1, 2。一共就是9桶。
注意如果左右两边的最大值中较小值小于等于该列高度，那么就无法倒水。
那么我们只需要用O(n)的复杂度维护一下每列左边的最大高度，和右边的最大高度，然后直接计算即可。
时间复杂度 O ( n ) O(n) O(n)。
代码：

#include<bits/stdc++.h>

using namespace std;

#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\n'

typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;


void Showball() {
  int n;
  cin>>n;
  vector<int> a(n),maxl(n),maxr(n);
  for(int i=0;i<n;i++){
    cin>>a[i];
  }
  maxl[1]=a[0];
  for(int i=2;i<n-1;i++){
    maxl[i]=max(maxl[i-1],a[i-1]);
  }
  maxr[n-2]=a[n-1];
  for(int i=n-3;i>0;i--){
    maxr[i]=max(maxr[i+1],a[i+1]);
  }
  int ans=0;
  for(int i=1;i<n-1;i++){
    //如果差值小于0，那么说明不能倒水，所以需要判断一下。
    ans+=max(0,min(maxl[i],maxr[i])-a[i]);
  }
  cout<<ans<<endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T = 1;
    //cin>>T;
    while(T--)
        Showball();
    return 0;
}

4. 三角形的个数

题意：给你一个三角形，将其没条边进行n等分，然后依次连接，求出连接后的三角形个数。
思路：遇到这种找规律的题目，我们就需要自己先手算几个进行分析。
n=2时：
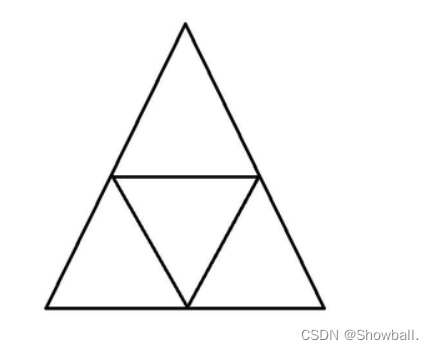
在这里插入图片描述
一共有5个三角形。
n=3时：
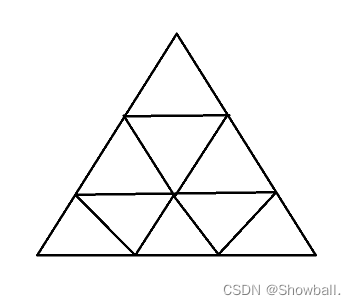
在这里插入图片描述

一共有13个三角形。
我们发现这些三角形有正有反。那么我们分开讨论一下。
对于正着放的三角形：
我们发现它的边长范围是：[1,n]
对于边长为 i i i的正放三角形，它在第 i i i层有1个。
那么最多可以到第n层，所以一共有 1 + 2 + . . . + n − i + 1 1+2+...+n-i+1 1+2+...+n−i+1个边长为 i i i的正放三角形。
对于前缀和，我们可以提前预处理好。
f[n]表示1-n之间所有数的和
那么总共的正三角形的个数就是 ∑ i = 1 n f [ n − i + 1 ] \sum\limits_{i=1}^n f[n-i+1] i=1∑n​f[n−i+1]
对于倒着放的三角形：
我们发现它的边长范围是：[1,n/2]
因为这个三角形是倒着放的，所以它需要预留一半的高度。
对于边长为 j j j的正放三角形，它在第 j j j层有1个。
最多到第 n − j n-j n−j层，有 ( n − j ) − j + 1 (n-j)-j+1 (n−j)−j+1个。
所以边长为 j j j的倒三角形一共有 1 + 2 + 3 + . . . ( n − 2 ∗ j + 1 ) 1+2+3+...(n-2*j+1) 1+2+3+...(n−2∗j+1)个。
那么总共的倒三角形的个数就是 ∑ j = 1 n / 2 f [ n − 2 ∗ j + 1 ] \sum\limits_{j=1}^{n/2} f[n-2*j+1] j=1∑n/2​f[n−2∗j+1]
两部分求和就是答案。
代码：

#include<bits/stdc++.h>

using namespace std;

#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\n'

typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;

int f[550];//存前缀和
void Showball() {
  int n;
  cin>>n;
  int ans=0;
  for(int i=1;i<=n;i++) ans+=f[n-i+1];
  for(int j=1;j<=n/2;j++) ans+=f[n-2*j+1];
  cout<<ans<<endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T = 1;
    cin>>T;
    //预处理前缀和
    for(int i=1;i<=500;i++) f[i]=f[i-1]+i;
    while(T--)
        Showball();
    return 0;
}

5. 硬币塔

题意：一个k级的硬币塔从下到上，由一个银币，一个k-1级硬币塔，一个k个金币，一个k-1级硬币塔，一个硬币构成。规定，0级硬币塔只有一个金币。
求出k级硬币塔从下往上数 i i i个，有几个金币。
思路:我们先梳理一下这个硬币塔的结构。
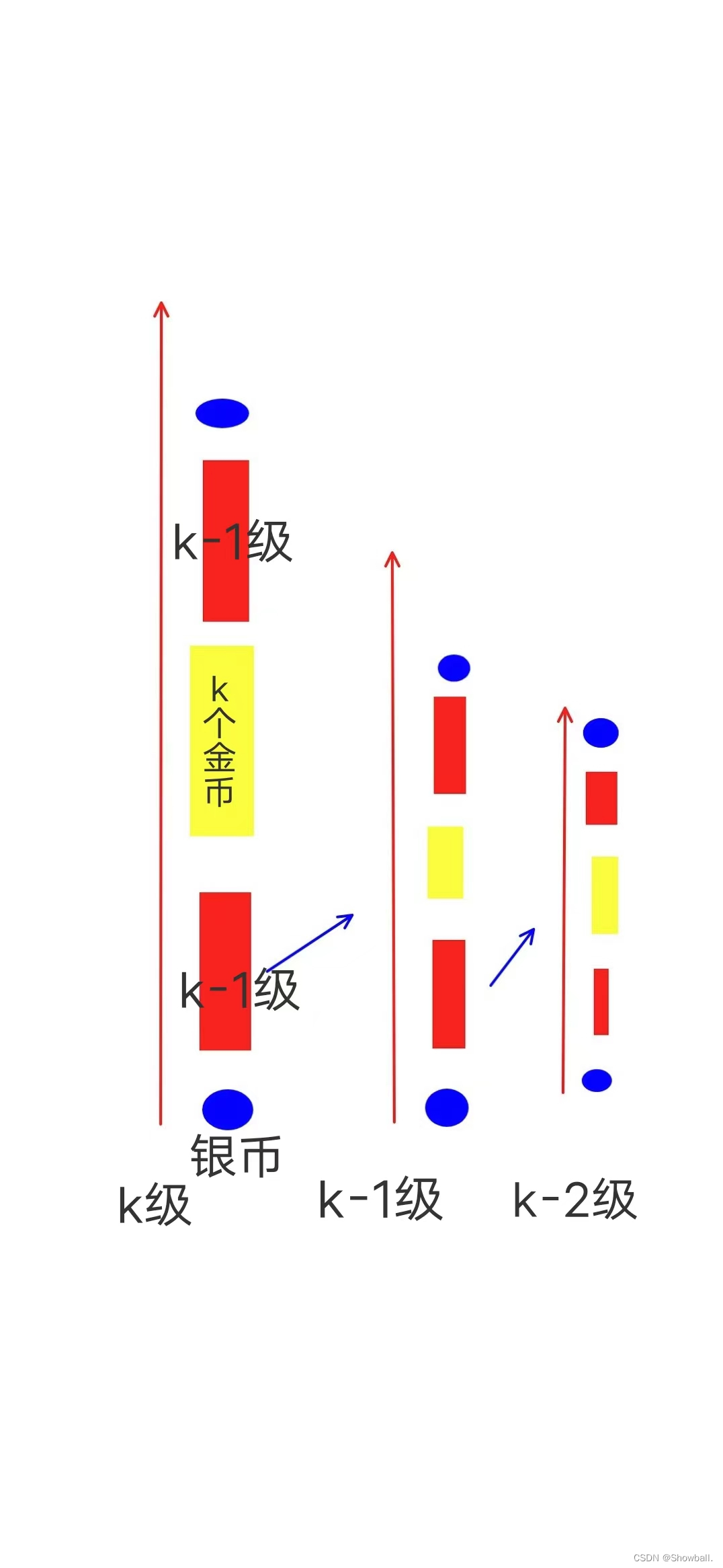
在这里插入图片描述
很明显是一个递归的结构，如果我们直接进行操作计数，也非常容易绕进去，以及出现各种各样的问题。
首先我们可以分析一下k级硬币塔的高度。定义一个数组 h [ N ] h[N] h[N],才存每级硬币塔的高度。我们已知 h [ 0 ] = 1 h[0]=1 h[0]=1,并且根据硬币塔的结构，很容易可以得到递推式： h [ i ] = 1 + h [ i − 1 ] + i + h [ i − 1 ] + 1 h[i]=1+h[i-1]+i+h[i-1]+1 h[i]=1+h[i−1]+i+h[i−1]+1。
这样我们就可以预处理出每级硬币塔的高度。然后我们就可以进行搜索了。这里为了防止超时我们可以对搜索进行一个记忆化，用一个map存一下已经搜索过的数据，这样就可以大大节省时间。
具体搜索过程可以参考代码和代码注释。
注意数据较大，开long long。
代码:

#include<bits/stdc++.h>

using namespace std;

#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\n'

typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;

map<pair<LL,LL>,LL> mp;//用来存取已经搜索过的结果
LL h[M];//存取高度
void init(){//预处理硬币塔高度
    h[0]=1;
    for(int i=1;i<=40;i++){
     h[i]=1+h[i-1]+i+h[i-1]+1;      
    }
}
LL dfs(LL a,LL b){//搜索，返回a级硬币塔往上数b个的金币数
  LL bb=b;
  //如果已经搜索过，直接返回
  if(mp.count({a,b})) return mp[{a,b}];
  if(a==0) return mp[{0,b}]=1;
  /*0级硬币塔只有一个金币，
  返回并且存在map中*/
  //1个银币
  b--;
  LL ans=0;
  //a-1级硬币塔
  if(b>0){
    LL t=min(h[a-1],b);
    b-=t;
    ans+=dfs(a-1,t);
  }
  //a个金币
  if(b>0){
    LL t=min(a,b);
    b-=t;
    ans+=t;
  }
  //a-1级硬币塔
  if(b>0){
    LL t=min(h[a-1],b);
    b-=t;
    ans+=dfs(a-1,t);
  }
  //1个银币
  b--;
  return mp[{a,bb}]=ans;//返回结果，并且存在map中。
}
void Showball() {
  LL k,i;
  cin>>k>>i;
  init();
  LL ans = 0;
  if(i) ans=dfs(k,i);
  cout<<ans<<endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T = 1;
    //cin>>T;
    while(T--)
        Showball();
    return 0;
}

码字不易，记得点赞 ^_^ 完结撒花~~~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/387521.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

cloud flare 真不错（常规思路）

cloud flare 真不错（常规思路）

2022-10-20 前言 接到一个测试目标&#xff0c;开局cloudflare&#xff0c;最后运气不错还是拿下了。因授权测试等原因&#xff0c;文章仅展示思路历程。 过程 信息搜集 给的目标是test.com&#xff0c;前期经过一些基本的信息搜集&#xff0c;发现了一个求职子域employee…
阅读更多...
FreeRTOS入门

FreeRTOS入门

目录 一、简介 二、堆的概念 三、栈的概念 四、从官方源码中精简出第一个FreeRTOS程序 五、修改官方源码增加串口打印 一、简介 FreeRTOS是一个迷你的实时操作系统内核。作为一个轻量级的操作系统&#xff0c;功能包括&#xff1a;任务管理、时间管理、信号量、消息队列、…
阅读更多...
嵌入式开发：McObject eXtremeDB嵌入式数据库系统

嵌入式开发：McObject eXtremeDB嵌入式数据库系统

嵌入式数据库已经成为数据库技术的一种流行应用&#xff0c;尤其是对于企业中的物联网应用。有很多理由将数据库嵌入到应用程序的端点中&#xff0c;而不仅仅是将数据推送到设备中。嵌入式开发人员在选择嵌入式数据库时&#xff0c;真正重要且与众不同的解决方案是写入速度、大…
阅读更多...
【边缘端环境配置】英伟达Jetson系列安装pytorch/tensorflow/ml/tensorrt环境（docker一键拉取）

【边缘端环境配置】英伟达Jetson系列安装pytorch/tensorflow/ml/tensorrt环境（docker一键拉取）

【边缘端环境配置】英伟达Jetson系列安装pytorch/tensorflow/ml/tensorrt环境&#xff08;docker一键拉取&#xff09;0.JetPack1.安装输入法2.安装docker和nvidia-docker3.拉取l4t-pytorch镜像4.拉取l4t-tensorflow镜像5.拉取l4t-ml镜像6.拉取tensorrt镜像7.镜像换源8.其他&am…
阅读更多...
三数之和(双指针 or hash表)

三数之和(双指针 or hash表)

给你一个整数数组nums &#xff0c;判断是否存在三元组 [nums[i], nums[j], nums[k]]满足 i ! j、i ! k 且 j ! k &#xff0c;同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意&#xff1a;答案中不可以包含重复的三元组。 3 < …
阅读更多...
ubuntu22.04 Desktop 服务器安装

ubuntu22.04 Desktop 服务器安装

操作系统 使用的是Uubntu22.04 Desktop的版本&#xff0c;系统安装后&#xff0c;默认开启了53端口和631端口 关闭udp 5353、53791端口&#xff08;avahi-daemon服务&#xff09; sudo systemctl stop avahi-daemon.socket avahi-daemon.service sudo systemctl disable ava…
阅读更多...
[1.2]计算机系统概述——操作系统的发展与分类

[1.2]计算机系统概述——操作系统的发展与分类

文章目录第一章 计算机系统概述操作系统的发展与分类&#xff08;一&#xff09;手工操作阶段&#xff08;二&#xff09;批处理阶段——单道批处理系统&#xff08;三&#xff09;批处理阶段——多道批处理系统&#xff08;四&#xff09;分时操作系统&#xff08;五&#xff…
阅读更多...
【Java开发】JUC进阶 01：Lock锁详解

【Java开发】JUC进阶 01：Lock锁详解

1 Lock锁介绍已经在【JUC基础】04简单介绍过了&#xff0c;本文做进一步的拓展&#xff0c;比如公平锁和非公平锁、&#x1f4cc; 明白锁的核心四个对象&#xff1a;线程&#xff0c;共享资源&#xff0c;锁&#xff0c;锁操作包括线程如何操作资源&#xff0c;使用锁锁哪个资源…
阅读更多...
xgboost： 分割查找算法:贪婪算法、分桶算法

xgboost： 分割查找算法:贪婪算法、分桶算法

1、Basic Exact Greedy Algorithm 树学习的关键问题之一是找到最好的分割&#xff0c;如Eq(7)所示。 贪婪算法:分割查找算法枚举所有特征上的所有可能的分割。精确的贪婪算法如Alg. 1所示。为了高效地完成这一任务&#xff0c;算法必须首先根据特征值对数据进行排序&#xff…
阅读更多...
SpringMVC 参数绑定（视图传参到控制器）

SpringMVC 参数绑定（视图传参到控制器）

✅作者简介&#xff1a;2022年博客新星 第八。热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏…
阅读更多...
Vue组件基础(父向子、子向父、子向子传值)

Vue组件基础(父向子、子向父、子向子传值)

Vue组件基础-父向子、子向父、子向子传值一、Vue组件概念,创建和使用1.1 组件概念1.2 组件基础使用1.3 组件-scoped作用二、Vue组件通信2.1 父向子传值(props)2.2 子向父传值($emit)2.3 子与子传值(EventBus)一、Vue组件概念,创建和使用 1.1 组件概念 组件是可复用的Vue实例,封…
阅读更多...
【100个 Unity实用技能】 | 脚本无需挂载到游戏对象上也可执行的方法

【100个 Unity实用技能】 | 脚本无需挂载到游戏对象上也可执行的方法

Unity 小科普 老规矩&#xff0c;先介绍一下 Unity 的科普小知识&#xff1a; Unity是 实时3D互动内容创作和运营平台 。包括游戏开发、美术、建筑、汽车设计、影视在内的所有创作者&#xff0c;借助 Unity 将创意变成现实。Unity 平台提供一整套完善的软件解决方案&#xff…
阅读更多...
springboot使用ssh公钥连接mysql（含账号密码连接）

springboot使用ssh公钥连接mysql（含账号密码连接）

引言 在项目开发过程中&#xff0c;遇到了连接数据库时需要使用ssh公钥的情况。在本地使用navicat可以直接通过可视化界面去进行ssh的连接&#xff0c;但是在java中无法直接去进行连接。 后来经过查询资料&#xff0c;发现必须要在java中编写相关配置文件后才可以正常连接。 …
阅读更多...
Linux内核源码进程原理分析

Linux内核源码进程原理分析

Linux内核源码进程原理分析一、Linux 内核架构图二、进程基础知识三、Linux 进程四要素四、task_struct 数据结构主要成员五、创建新进程分析六、剖析进程状态迁移七、写时复制技术一、Linux 内核架构图 二、进程基础知识 Linux 内核把进程称为任务(task)&#xff0c;进程的虚…
阅读更多...
Linux下MQTT客户端消息订阅与发布实现

Linux下MQTT客户端消息订阅与发布实现

MQTT(消息队列遥测传输)是一个基于客户端-服务器的消息发布/订阅传输协议。它基于TCP协议&#xff0c;默认端口号为1883&#xff0c;为此&#xff0c;它也需要一个消息中间件 。MQTT协议是轻量、简单、开放和易于实现的&#xff0c;这些特点使它适用范围非常广泛。在很多情况下…
阅读更多...
蓝桥杯三月刷题 第一天

蓝桥杯三月刷题 第一天

文章目录&#x1f4a5;前言&#x1f609;解题报告&#x1f4a5;数列求值&#x1f914;一、思路:&#x1f60e;二、代码&#xff1a;&#x1f4a5;质数&#x1f914;一、思路:&#x1f60e;二、代码&#xff1a;&#x1f4a5;饮料换购&#x1f914;一、思路:&#x1f60e;二、代…
阅读更多...
23.3.4打卡 AtCoder Beginner Contest 291（Sponsored by TOYOTA SYSTEMS）A~E

23.3.4打卡 AtCoder Beginner Contest 291（Sponsored by TOYOTA SYSTEMS）A~E

F题题面都看不懂嘞!开摆! 没找到合适的markdown, 截图网页翻译了我真是天才 比赛链接: https://atcoder.jp/contests/abc291 A题 题意 给出一个字符串, 找到第一个大写字母的下标 简单题就不多说了, 直接放代码 代码 void solve() {cin>>str;nstr.size();str"…
阅读更多...
CentOS7操作系统安装nginx实战（多种方法，超详细）

CentOS7操作系统安装nginx实战（多种方法，超详细）

文章目录前言一. 实验环境二. 使用yum安装nginx2.1 添加yum源2.1.1 使用官网提供的源地址&#xff08;方法一&#xff09;2.1.2 使用epel的方式进行安装&#xff08;方法二&#xff09;2.2 开始安装nginx2.3 启动并进行测试2.4 其他的一些用法&#xff1a;三. 编译方式安装ngin…
阅读更多...
Kali、Metasploitable2部署

Kali、Metasploitable2部署

1、安装VMWare虚拟机及metasploitable2软件 链接&#xff1a;https://pan.baidu.com/s/1rqhjh1P9VJg5Q1esBgpZ-A 提取码&#xff1a;dc66 metasploitable2部署很简单&#xff0c;解压后&#xff0c;直接双击后缀.vmx文件&#xff0c;默认账户msfadmin/msfadmin&#xff0c;sud…
阅读更多...
php实训报告

php实训报告

实训一 PHP语法基础 一、实训目的 掌握PHP数据类型知识。掌握PHP变量与常量的知识和运用方法。掌握PHP选择结构流程控制的知识及应用。掌握PHP循环结构流程控制的知识及应用。 二、实训工具或设备 主流 PC 机一台&#xff08;要求安装 windows 操作系统&#xff09;&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023