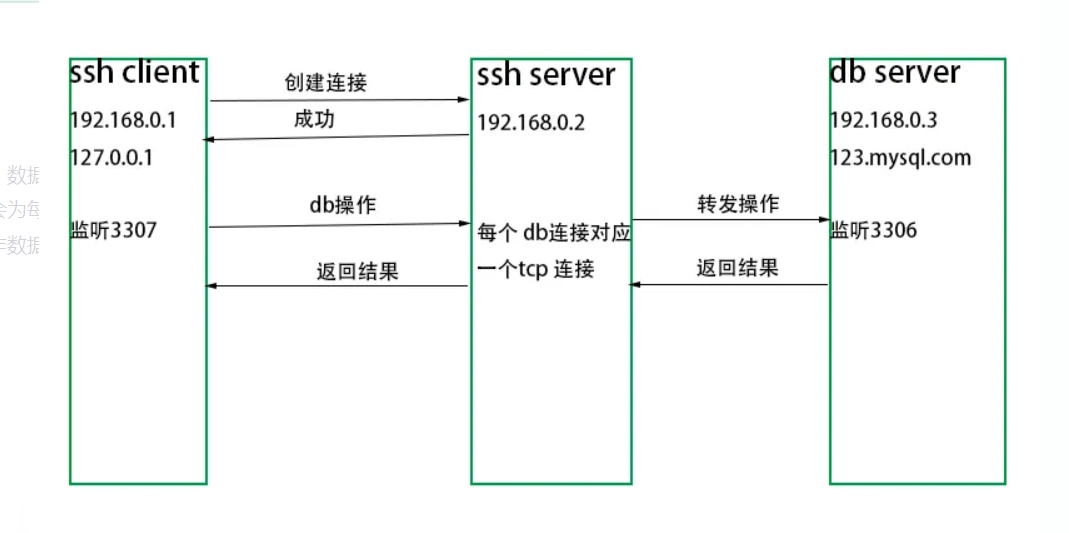
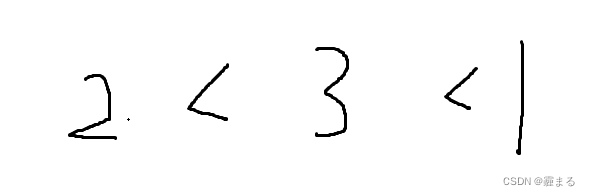给你一个整数数组nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]]满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

3 <= nums.length <= 3000
-105 <= nums[i] <= 105

解法：双指针（复杂度$O(N^2)$）

思路：

       我们可以将num[i] + num[j] + num[k] = 0转换为num[i] + num[j] = -num[k]。那么其实问题就变成了找到和为-num[k]的二元组的问题（这个问题是经典的两数之和问题，可以排序后用双指针解决，也可以用哈希表解决，我们这里使用双指针）。

        我们需要遍历去k，对于每一个k找出对应的符合条件的二元组。难点在于怎么样去除掉符合条件的重复的三元组(i, j, k)。

        如果我们先将所有符合条件的三元组求出，然后再进行去重的话，量级会很大，比如当所有数都为0时，如:[0,0,0,0,0……0]，如果此时的$n$大小为3000的话，满足的三元组数量将会达到恐怖的$C_{3000}^3$，将近4e9的大小，复杂度太太高。所以我们必须在遍历时就去重，怎么做呢？

        如果我们想对最终得到的(num[i], num[j], num[k])三元组去重，那么遍历的时候就需要对num[i]，num[j], num[k]都去重。具体详情见代码。

详细思路如下图:

代码：

#include <vector>
class Solution {
  public:
    vector<vector<int>> threeSum(vector<int>& num) {
        int n = num.size();
        vector<vector<int>> ans;
        sort(num.begin(), num.end());
        for (int k = 0; k < n; ++ k) {
        	//去重k
            if(k != 0 && num[k] == num[k - 1]) continue;
            int i = k + 1, j = n - 1;  
            int target = -num[k];
            while(i < j) {
                if (i < n - 1 && (num[i] + num[j] < target)) {
                    i ++;
                } else if (j > 1 && (num[i] + num[j] > target)) {
                    j --;
                } else {   //num[i] + num[j] = -num[k]
                    if (i != k && j != k) {
                        vector<int> temp;
                        temp.push_back(num[i]);
                        temp.push_back(num[j]);
                        temp.push_back(num[k]);
                        sort(temp.begin(), temp.end());
                        ans.push_back(temp);
                    }
                    //去重i
                    while(i + 1 < n - 1 && num[i] == num[i + 1]) i ++;
                    //去重j
                    while(j - 1 > 0 && num[j] == num[j - 1]) j --;
                    if (i < j) {
                        i ++, j --;  //如果当前是符合条件的二元组，那么就将i，j都挪动一次，因为去此时已经去完重了，
                        //如果num[i] + num[j] = target, 那么num[i] + num[p](0 =< p < j) 不可能等于target，其和只会越来越小;
                        //同理对于num[p] + num[j](n > p > i)也是一样的。所以对于同一个k来说，符合条件的i，j一定不会再被放入二元组当中。
                    }
                }
            }
        }
        return ans;
    }
};
// num[a] + num[b] == -num[c]