【算法基础】排序插入、归并、堆、快速升序+降序

news2025/2/26 14:23:03

1.排序

1.1 插入排序

1.2 归并排序

1.3 推排序

1.4 快速排序

1.排序

1.1 插入排序

时间复杂度：O(n)~O(n*n)
空间复杂度：O(1)
稳定

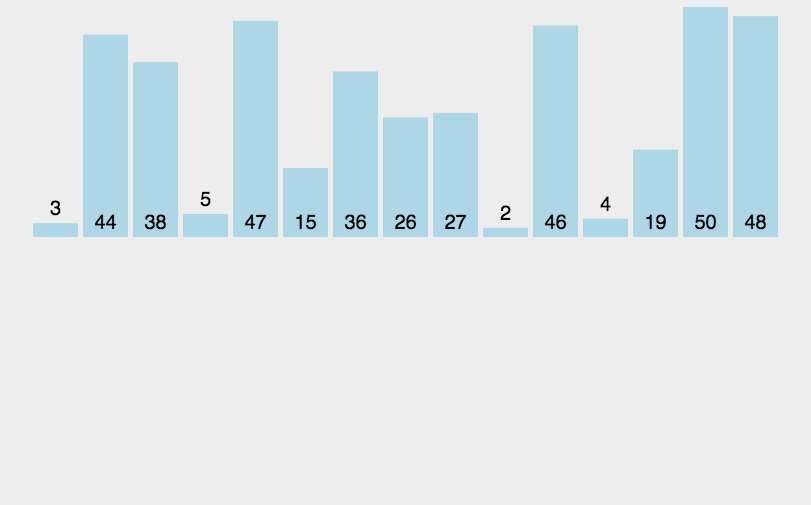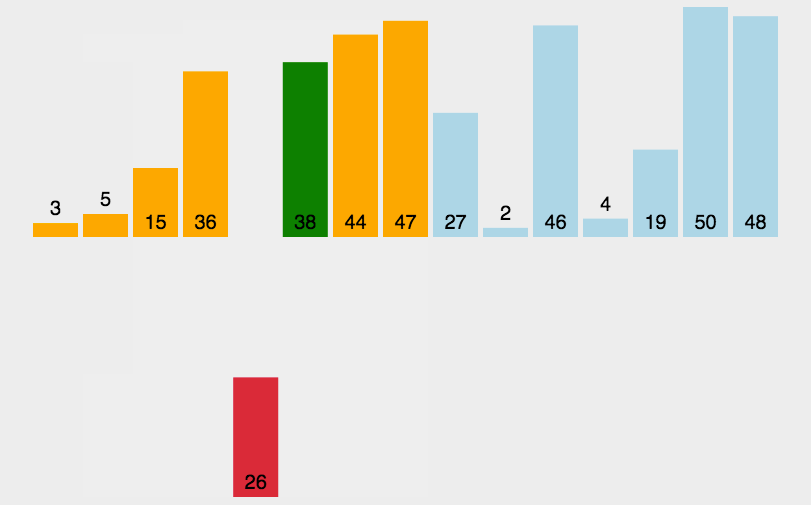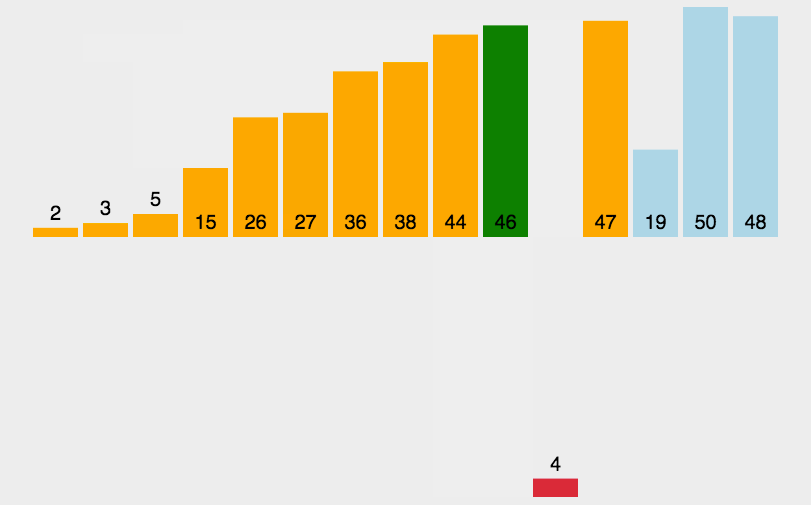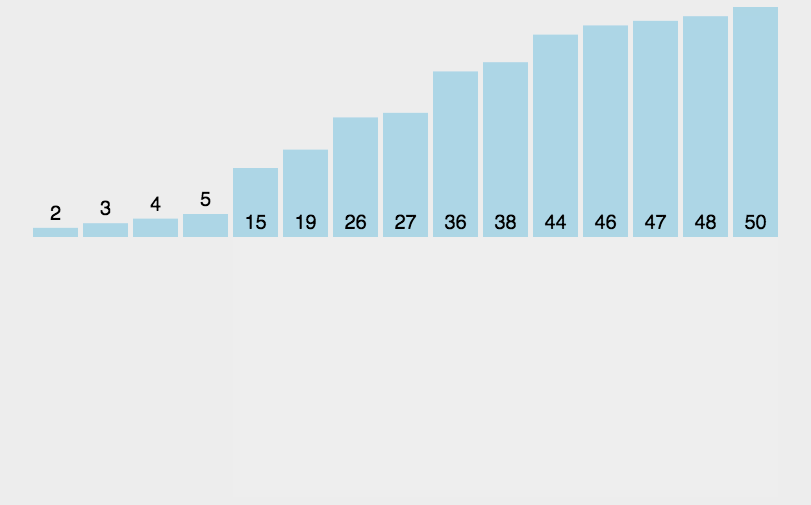
步骤：

1.设第一个元素为有序列。

2.取有序列后面的一个元素。

3.将该元素插入到有序列中的正确位置。

4.依次重复3、4步，直到完成排序。

#include<iostream>
using namespace std;

//插入升序
void insert_sort_asc(int* arr, int n)
{
     for (int i = 0; i < n - 1; i++)
     {
          int end = i;//有序列的最后一个元素
          int temp = arr[end + 1];//当前需要插入排序的元素

          while (end>=0)//最坏情况下，遍历至有序列的第一个元素
          {
               if (temp < arr[end]) //待插入的数小，就将大数往后移
               {
                    arr[end + 1] = arr[end];//后移
                    end--;//向前继续找位置
               }
               else
               {
                    break;//temp更大，则找到要插入的位置，退出循环
               }
          }
          arr[end+1] = temp;//temp插在较小数后
     }
}

//插入降序
void insert_sort_dec(int* arr, int n)
{
     for (int i = 0; i < n - 1; i++)
     {
          int end = i;
          int temp = arr[end+1];
          while (end>=0)
          {
               if (temp > arr[end])
               {
                    arr[end + 1] = arr[end];
                    end--;
               }
               else
               {
                    break;
               }
          }
          arr[end + 1] = temp;
     }
}

void output(int* arr, int n)
{
     for (int i = 0; i < n; i++)
     {
          cout << arr[i] << " ";
     }
     cout << endl;
}

int main()
{
     int n, arr[99],copy[99];
     cout << "Number of inputs:";
     cin >> n;
     cout << "Inputs array:";
     for (int i = 0; i < n; i++)
     {
          cin >> arr[i];
     }
     memcpy(copy, arr, n * sizeof(int));

     insert_sort_asc(copy, n);
     output(copy, n);
     insert_sort_dec(arr, n);
     output(arr, n);
}

1.2 归并排序

时间复杂度：O(n\log n)
时间复杂度：O(n)
稳定

正在上传…

重新上传

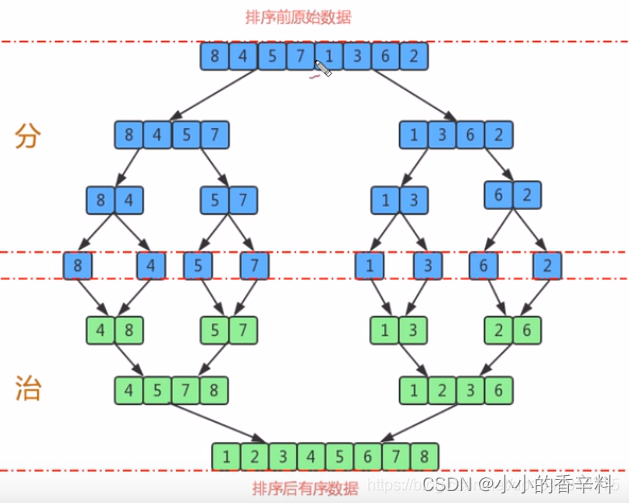
分治算法

分：将数组分为各小部分。

治：各小部分排序。
- 步骤
  - 分的步骤：
    
    1.计算中点mid；
    
    2.将mid左边和右边递归继续分，直到分到每一小部分只有一个元素；
    
    3.结合每两个小部分排序，直到所有分开的部分重新合起来。
  - 治的步骤（排序的步骤）：
    
    1.取要合并的两部分首元素，比较大小；
    
    2.若升序排列，则取两部分中较小的一个，加入新数组；
    
    3.重复1，2步骤，直到有一部分被全部取完。

#include<iostream>
using namespace std;
#define N 9999

void merger_sort_asc(int* arr, int l, int r);
void merger_sort_dec(int* arr, int l, int r);

void process_asc(int* arr, int l, int r)
{
     if (l == r)return;//分到最小时返回（每组只有一个元素）

     //计算中点时不用(r+l)/2,是为了防止r+l溢出
     int mid = l + (r - l) / 2;//计算中点
     process_asc(arr, l, mid);//继续分治左部分
     process_asc(arr, mid + 1, r);//继续分治右部分
     merger_sort_asc(arr, l,r);//各部分排序
}

void merger_sort_asc(int* arr, int l,int r)
{
     int mid = l + (r - l) / 2;
     int i = l;//第一部分首元素
     int j = mid + 1;//第二部分首元素
     int temp[N];//临时数组存放
     int k = 0;//临时数组下标

     //比较
     while (i <= mid && j <= r)
     {
          //两部分中首元素比大小，哪个小就把哪个放入临时数组
          temp[k++] = (arr[i] < arr[j]) ? arr[i++] : arr[j++];
     }

     //若其中一部分已经取完，另外一部分有剩余元素
     while (i<=mid)
     {
          temp[k++] = arr[i++];
     }
     while (j <= r)
     {
          temp[k++] = arr[j++];
     }

     //把排好序的临时数组放入原数组
     for (int t = l; t <= r; t++)
     {
          arr[t] = temp[t-l];//原数组下标从l开始，临时数组从0开始
     }
}


void process_dec(int* arr, int l, int r)
{
     if (l == r)return;
     int mid = l + (r - l) / 2;
     process_dec(arr, l, mid);
     process_dec(arr, mid + 1, r);
     merger_sort_dec(arr, l, r);
}

void merger_sort_dec(int* arr, int l, int r)
{
     int mid = l + (r - l) / 2;
     int i = l, j = mid + 1;
     int k = 0, temp[N];

     while (i <= mid && j <= r)
     {
          temp[k++] = (arr[i] > arr[j]) ? arr[i++] : arr[j++];
     }
     while (i <= mid)
     {
          temp[k++] = arr[i++];
     }
     while (j <= r)
     {
          temp[k++] = arr[j++];
     }

     for (int t = l; t <= r; t++)
     {
          arr[t] = temp[t - l];
     }
}

void output(int* arr,int n)
{
     for (int i = 0; i < n; i++)
     {
          cout << arr[i]<<" ";
     }
     cout << endl;
}

int main()
{
     int n;
     int arr[N],copy[N];
     cout << "The number of input:";
     cin >> n;
     cout << "Input the array:";
     for (int i = 0; i < n; i++)
     {
          cin >> arr[i];
     }
     memcpy(copy, arr, n * sizeof(int));

     process_asc(arr, 0, n - 1);
     output(arr, n);

     process_dec(copy, 0, n - 1);
     output(copy, n);
}

*分治核心思想

使用场景：大问题难以解决，小问题容易解决。

1.把大问题拆解成小问题（递归）。 2.处理每个小问题。 3.合并每个小问题，解决大问题（递归）。

1.3 推排序

a.堆

分类：
- 大根堆：父结点比左孩子和右孩子大。
- 小根堆：父结点比左孩子和右孩子小。
在数组中表示：

b.堆排序

性能

空间复杂度：O(1)

时间复杂度：O(nlogn)

不稳定
排序步骤

升序大根堆，降序小根堆。

1.将数组构造成大根堆（堆顶==最大值）；

2.将堆顶与堆末交换，相当于把堆分为没有排好序的堆顶和排好序的堆尾；

3.将剩余n-1个数再构造成大根堆；

4.将堆顶与n-1处的数交换；

5.如此重复，直到排完。
构造大根堆步骤

1.从最后一棵子树开始比较（从后往前）；

2.通过父结点和子结点值的交换，将每棵子树的最大值作为父结点（从上到下）；

3.直到构成大根堆。

#include<iostream>
#include<algorithm>
using namespace std;

//降序
//调整当前小堆，parent是小堆堆顶
void down(int* arr, int parent,int n)
{
     //定义这个子堆中的父子
     int child = parent * 2 + 1;//左孩子

     //孩子超过数组下标结束
     while (child < n)
     {
          //保证child是左右孩子中最小的
          //且要保证有右孩子
          if (child + 1 < n && arr[child + 1] < arr[child])
          {
               child++;
          }
          //小的往上，大的往下
          if (arr[child] < arr[parent])
          {
               swap(arr[child], arr[parent]);//换父子值
               //换父子下标
               parent = child;
               child = parent * 2 + 1;
          }
          else
          {
               break;
          }
     }
}
void heap_sort_dec(int* arr, int n)
{
     //建小堆
     //从最后一个小堆开始，i是小堆父结点
     for (int i = (n-2) / 2; i>=0; i--)
     {
          down(arr,i,n);
     }
     int end=n-1;
     while (end>0)
     {
          swap(arr[end], arr[0]);//交换堆顶（用最后一个数覆盖第一个）
          down(arr, 0, end--);//新堆再造小根堆
     }
}

//升序
void up(int* arr, int parent, int n)
{
     int child = parent*2+1;
     while (child <n)
     {
          //选出最大孩子
          if (child + 1 < n && arr[child + 1] > arr[child])
          {
               child++;
          }
          //小的往下，大的往上
          if (arr[child] > arr[parent])
          {
               swap(arr[child], arr[parent]);//换父子值
               //换父子下标
               parent = child;
               child = parent * 2 + 1;
          }
          else
          {
               break;
          }
     }
}
void heap_sort_asc(int* arr, int n)
{
     for (int i = (n-2)/2; i >=0; i--)
     {
          up(arr, i, n);
     }
     int end = n - 1;
     while (end > 0)
     {
          swap(arr[0], arr[end]);
          up(arr, 0, end);
          end--;
     }
}

void output(int* arr, int n)
{
     for (int i = 0; i < n; i++)
     {
          cout << arr[i] << " ";
     }
     cout << endl;
}

int main()
{
     int n,arr[999],copy[999];
     cin >> n;
     for (int i = 0; i < n; i++)
     {
          cin >> arr[i];
          copy[i] = arr[i];
     }
     heap_sort_asc(arr, n);
     output(arr, n);
     heap_sort_dec(copy, n);
     output(copy, n);
}

1.4 快速排序

主要思想：冒泡排序的分治。
步骤： 1.确定分界点x，为 x=q [ （left+right) / 2 ] ； 2.调整数组，使之成为
调整方法：1) i从left开始向右找>=x的数，得q[ i ]； 2) j从left开始向左找<=x的数，得q[ j ]； 3)如果 i<j ，说明还没有调整完成，则交换q[ i ] and q[ j ]；若 i>=j 说明已经调整完。

3.x左右两边递归。

#include<iostream>
#include<algorithm>
using namespace std;

//升序
void quick_sort_asc(int* arr, int l, int r)
{
     if (l >= r)return;
     int x = arr[l + (r - l) / 2];
     int i = l - 1, j = r + 1;
     while (i < j)
     {
          //找出左边大于x的数组下标i
          do i++; while (arr[i] < x);
          //找出右边小于x的数组下标j
          do j--; while (arr[j] > x);
          //如果左右都找到了符合条件的值
          if (i < j)
          {
               swap(arr[i], arr[j]);
          }
     }
     quick_sort_asc(arr, l, j);
     quick_sort_asc(arr, j + 1, r);
}

//降序
void quick_sort_dec(int* arr, int l, int r)
{
     if (l >= r)return;
     int i = l - 1, j = r + 1;
     int x = arr[l + (r - l) / 2];
     while (i < j)
     {
          do i++; while (arr[i] > x);
          do j--; while (arr[j] < x);
          if (i < j)
          {
               swap(arr[i], arr[j]);
          }
     }
     quick_sort_dec(arr, l, j);
     quick_sort_dec(arr, j + 1, r);
}

void output(int* arr, int n)
{
     for (int i = 0; i < n; i++)
     {
          cout << arr[i]<<" ";
     }
     cout << endl;
}

int main()
{
     int n, arr[999];
     cin >> n;
     for (int i = 0; i < n; i++)
     {
          cin >> arr[i];
     }
     quick_sort_asc(arr, 0, n - 1);
     output(arr, n);
     quick_sort_dec(arr, 0, n - 1);
     output(arr, n);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/387014.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！