设计跳表(动态设置节点高度)

news2024/12/23 20:35:13

最近学习redis的zset时候，又看到跳表的思想，突然对跳表的设置有了新的思考
这是19年设计的跳表，在leetcode的执行时间是200+ms
现在我对跳表有了新的想法
1、跳表的设计，类似二分查找，但是不是二分查找，比较像之前遇到的一个面试题，使用有限个数鸡蛋，确定鸡蛋易损程度
2、跳表无法再设计的时候，就达到完美状态，而是在操作过程中一直维护完美状态
基于以上想法，我开始重新进行跳表的设计，在leetCode执行时间为14ms
设计思路如下：
0、设计节点，节点有next和pre两个指针，且因为多层结构，所以是数组表达
1、设计多层数据结构，多层均为有序链表，其中第0层包含所有数值
2、初始时，只有一层结构，先设计为10层结构
3、新增数据时，如果发现步数(即执行next次数)过长(大于3倍层高)，就进行抬升节点高度行为，即节点high值增加

最初代码如下：
Node类

		class Node {
            Node[] next = new Node[10];
            Node[] pre = new Node[10];
            //节点高度
            int high = 0;
            //节点值
            int value;
            //最近一次走到这个节点的步数
            int step = 0;
            //这个仅是为了后续show方法使用
            int k = 0;
        }

基础参数及构造器

		//头节点
        Node head;
        int maxHigh = 0;
        //步数
        int step = 0;

        public Skiplist() {
        }

查询操作，不直接查是否有，而是查floor值后，与tagert进行比较，查floor作用是，复用

public boolean search(int target) {
    if (head == null) {
        return false;
    }
    if (head.value > target) {
        return false;
    }
    //查询Floor
    return searchFloor(head, maxHigh, target).value == target;
}


private Node searchFloor(Node node, int high, int target) {
    //查到了
    if (node.value == target) {
        return node;
    }
    //已经最下层了
    if (high == -1) {
        return node;
    }
    //如果next值小于tagert,就进行next操作
    while (node.next[high] != null &&
            node.next[high].value <= target) {
        //步数增加
        step++;
        node = node.next[high];
        node.step = step;
    }
    //向下找
    return searchFloor(node, high - 1, target);
}

新增节点

public void add(int num) {
    if (head == null) {
        head = new Node();
        head.value = num;
        //没有head，好处理
        return;
    }
    if (num < head.value) {
        Node newHead = new Node();
        newHead.value = num;
        //比head还小，加上之后，充当新head
        setNewHead(newHead, head);
        return;
    }
    step = 0;
    Node newNode = new Node();
    newNode.value = num;
    //找到floor，就加在floor后面
    Node node = searchFloor(head, maxHigh, num);
    setNext(node, newNode);
    if (step > 3 * maxHigh) {
        //需要抬高高度了，这个方法很重要，类似hashmap的扩容
        resize(newNode);
    }
}

先把几个简单的方法展示出来

		private void setNext(Node pre, Node node) {
            int high = node.high;
            if (pre.next[high] == null) {
                pre.next[high] = node;
                node.pre[high] = pre;
            } else {
                Node next = pre.next[high];
                pre.next[high] = node;
                node.pre[high] = pre;
                node.next[high] = next;
                next.pre[high] = node;
            }
        }
        
        private void setNewHead(Node newHead, Node head) {
            newHead.high = head.high;
            for (int i = 0; i <= newHead.high; i++) {
                newHead.next[i] = head;
                head.pre[i] = newHead;
            }
            this.head = newHead;
        }

重点在resize

		private void resize(Node node) {
            if (node.high == maxHigh) {
                //如果当前高度已经是最高高度了，将maxHigh增高
                maxHigh++;
                if (maxHigh == 10) {
                    show();
                }
                node.high = maxHigh;
                head.high = maxHigh;
                head.next[maxHigh] = node;
                node.pre[maxHigh] = head;
                return;
            }
            //找前者
            Node pre = getMoreHighPre(node);
            //抬高高度
            node.high++;
            //加入节点(比如，开始加在0层，这时就记在1层)
            setNext(pre, node);
            //更新步数值
            node.step = pre.step + 1;
            //步数还大，继续增高
            if (node.step > 3 * (maxHigh + 1)) {
                resize(node);
            }
        }

        private Node getMoreHighPre(Node node) {
            int high = node.high;
            Node pre = node.pre[high];
            //找到高一层级的上一个节点
            while (pre.high == high) {
                pre = pre.pre[high];
            }
            return pre;
        }

删除操作

		public boolean erase(int num) {
            if (head == null) {
                return false;
            }
            if (head.value == num) {
                if (head.next[0] != null && head.next[0].value == num) {
                    //能不删head尽量不删head
                    removeNode(head.next[0]);
                } else {
                    //只能删除head
                    removeHead();
                }
                return true;
            }
            //一样，找到对应节点
            Node node = searchFloor(head, maxHigh, num);
            if (node.value == num) {
                //移除
                removeNode(node);
                return true;
            }
            return false;
        }

        private void removeNode(Node node) {
            for (int i = 0; i <= node.high; i++) {
                //每一层，都要删除
                Node pre = node.pre[i];
                Node next = node.next[i];
                if (next == null) {
                    //注意可能没有next
                    pre.next[i] = null;
                } else {
                    pre.next[i] = next;
                    next.pre[i] = pre;
                }
            }
        }

        private void removeHead() {
            //删除头节点，就是把老二当老大用
            if (head.next[0] == null) {
                head = null;
            }
            Node node = head.next[0];
            node.high = head.high;
            for (int i = 1; i <= maxHigh; i++) {
                if (head.next[i] != null && head.next[i] != node) {
                    node.next[i] = head.next[i];
                    head.next[i].pre[i] = node;
                }
            }
            head = node;
        }

以上代码执行后，leetCode执行时长为19ms，已经远快于19年的代码
但是，我发现了问题所在
因为数组高度有限，设置的高度为10，如果高度不够，就会出现数组越界，我尝试进行测试，写了show方法

		private void show() {
            System.out.println("总数"+i+"为出现越界");
            System.out.println("0级，并设置k");
            head.k = 0;
            int k = 0;
            Node node = head;
            while (node != null) {
                node.k = k++;
                node = node.next[0];
            }
            for (int i = 1; i < 10; i++) {
                System.out.println(i + "级间隔：");
                node = head;
                Node next = node.next[i];
                while (next != null) {
                    System.out.print(next.k - node.k + ",");
                    node = next;
                    next = node.next[i];
                }
                System.out.println();
            }
        }

结果如下
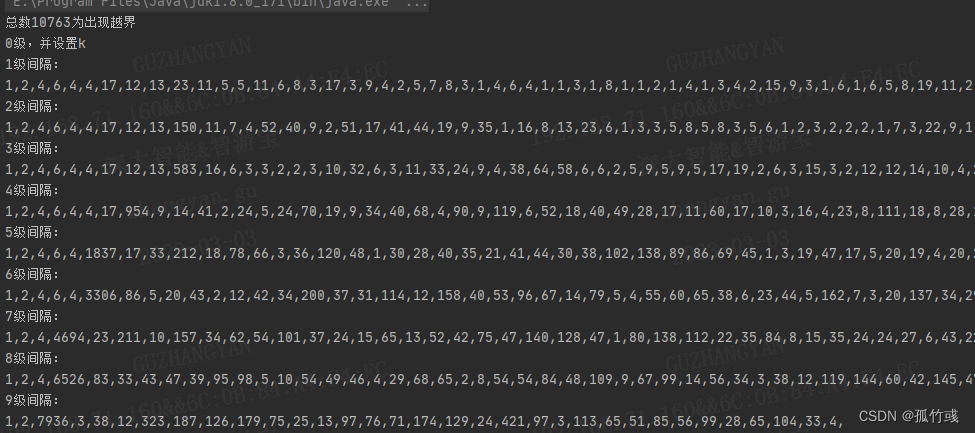
在这里插入图片描述
居然一万多数值之后就越界了，思考原因所在
应该是，抬高的node，不应该是插入的那个node，应该是node所在层次的中间node，调整接口如下

通过middleNode，找到需要抬高的node

private void resize(Node node) {
    if (node.high == maxHigh) {
        //最高层，这个可以接受
        maxHigh++;
        if (maxHigh == max) {
            show();
        }
        node.high = maxHigh;
        head.high = maxHigh;
        head.next[maxHigh] = node;
        node.pre[maxHigh] = head;
        return;
    }
    //找前人
    Node pre = getMoreHighPre(node);
    //不应该直接用node升级，应该用node区间的中间值
    node = middleNode(pre, node);
    node.high++;
    //加入节点
    setNext(pre, node);
    node.step = pre.step + 1;
    if (node.step > 3 * (maxHigh + 1)) {
        resize(node);
    }
}

寻找middleNode的代码如下

private Node middleNode(Node pre, Node node) {
    int high = node.high;
    if (pre.next[high + 1] == null) {
        return getLast(node);
    }
    Node next = pre.next[high + 1];
    int left = getLen(pre, node, node.high);
    int right = getLen(node, next, node.high);
    if (left == right) {
        return node;
    }
    if (left > right) {
        return left(node, (left - right) / 2);
    } else {
        return right(node, (right - left) / 2);
    }
}

private int getLen(Node left, Node right, int high) {
    int step = 0;
    while (left != right) {
        left = left.next[high];
        step++;
    }
    return step;
}

private Node left(Node node, int step) {
    if (step == 0) {
        return node;
    }
    return left(node.pre[node.high], step - 1);
}

private Node right(Node node, int step) {
    if (step == 0) {
        return node;
    }
    return right(node.next[node.high], step - 1);
}

private Node getLast(Node node) {
    int high = node.high;
    while (node.next[high] != null) {
        node = node.next[high];
    }
    return node;
}

同时发现，最左侧有一些数字极低值，优化setNewHead方法

		private void setNewHead(Node newHead, Node head) {
            newHead.high = head.high;
            newHead.next[0] = head;
            head.pre[0] = newHead;
            head.high = 0;
            for (int i = 1; i <= newHead.high; i++) {
                Node next = head.next[i];
                if(next==null){
                    break;
                }
                newHead.next[i] = next;
                next.pre[i] = newHead;
            }
            this.head = newHead;
        }

执行leetCode，14ms
在这里插入图片描述

使用show方法
结果如下：
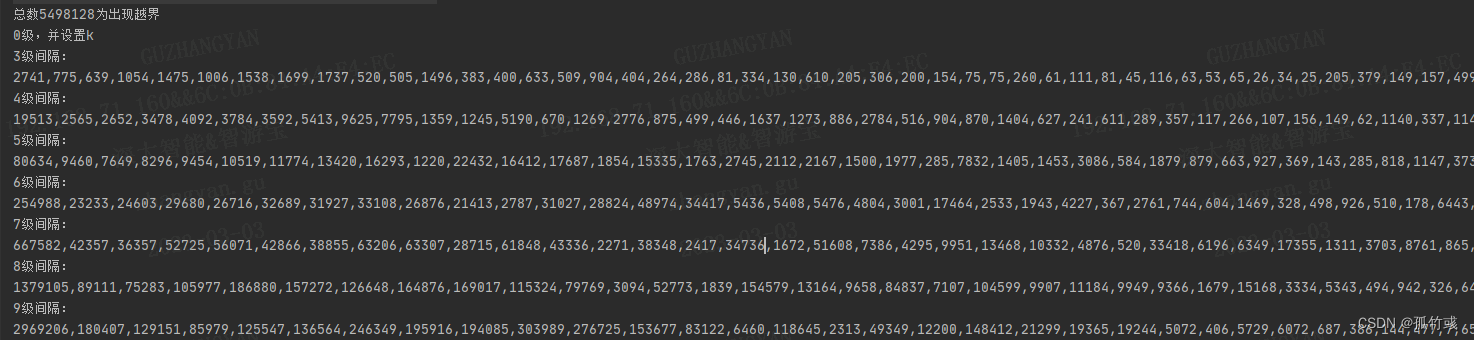
在这里插入图片描述
数据超过我的想象，百万级了
当然，这不是完美的跳表，比如我只在新增时，判断是否需要抬高(resize),查询时没有，可能出现某些节点运气不好，查询就是很慢

完整代码包括test在下方

public class TiaoBIaoNewTest {
    static int i =0;

    public static void main(String[] args) {
        Skiplist skiplist = new Skiplist();
        Random random = new Random();
        for (i = 0; i < 1000000000; i++) {
            skiplist.add(random.nextInt());
        }
        System.out.println();
    }

    static class Skiplist {

        static int max = 10;
        class Node {
            Node[] next = new Node[max];
            Node[] pre = new Node[max];
            int high = 0;
            int value;
            //最近一次走到这个节点的步数
            int step = 0;
            int k = 0;
        }

        Node head;
        int maxHigh = 0;

        //1)先分割0级
        public Skiplist() {
        }

        public boolean search(int target) {
            if (head == null) {
                return false;
            }
            if (head.value > target) {
                return false;
            }
            Node node = searchFloor(head, maxHigh, target);
            return node.value == target;
        }

        int step = 0;

        private Node searchFloor(Node node, int high, int target) {
            if (node.value == target) {
                return node;
            }
            if (high == -1) {
                return node;
            }
            while (node.next[high] != null &&
                    node.next[high].value <= target) {
                step++;
                node = node.next[high];
                node.step = step;
            }
            return searchFloor(node, high - 1, target);
        }


        public void add(int num) {
            if (head == null) {
                head = new Node();
                head.value = num;
                return;
            }
            if (num < head.value) {
                Node newHead = new Node();
                newHead.value = num;
                setNewHead(newHead, head);
                return;
            }
            step = 0;
            Node newNode = new Node();
            newNode.value = num;
            Node node = searchFloor(head, maxHigh, num);
            setNext(node, newNode);
            if (step > 3 * maxHigh) {
                resize(newNode);
            }
        }

        private void setNewHead(Node newHead, Node head) {
            newHead.high = head.high;
            newHead.next[0] = head;
            head.pre[0] = newHead;
            head.high = 0;
            for (int i = 1; i <= newHead.high; i++) {
                Node next = head.next[i];
                if(next==null){
                    break;
                }
                newHead.next[i] = next;
                next.pre[i] = newHead;
            }
            this.head = newHead;
        }

        public boolean erase(int num) {
            if (head == null) {
                return false;
            }
            if (head.value == num) {
                if (head.next[0] != null && head.next[0].value == num) {
                    removeNode(head.next[0]);
                } else {
                    removeHead();
                }
                return true;
            }
            Node node = searchFloor(head, maxHigh, num);
            if (node.value == num) {
                removeNode(node);
                return true;
            }
            return false;
        }

        private void removeNode(Node node) {
            for (int i = 0; i <= node.high; i++) {
                Node pre = node.pre[i];
                Node next = node.next[i];
                if (next == null) {
                    pre.next[i] = null;
                } else {
                    pre.next[i] = next;
                    next.pre[i] = pre;
                }
            }
        }

        private void removeHead() {
            if (head.next[0] == null) {
                head = null;
            }
            Node node = head.next[0];
            node.high = head.high;
            for (int i = 1; i <= maxHigh; i++) {
                if (head.next[i] != null && head.next[i] != node) {
                    node.next[i] = head.next[i];
                    head.next[i].pre[i] = node;
                }
            }
            head = node;
        }

        private void resize(Node node) {
            if (node.high == maxHigh) {
                //最高层，这个可以接受
                maxHigh++;
                if (maxHigh == max) {
                    show();
                }
                node.high = maxHigh;
                head.high = maxHigh;
                head.next[maxHigh] = node;
                node.pre[maxHigh] = head;
                return;
            }
            //找前人
            Node pre = getMoreHighPre(node);
            //不应该直接用node升级，应该用node区间的中间值
            node = middleNode(pre, node);
            node.high++;
            //加入节点
            setNext(pre, node);
            node.step = pre.step + 1;
            if (node.step > 3 * (maxHigh + 1)) {
                resize(node);
            }
        }

        private Node middleNode(Node pre, Node node) {
            int high = node.high;
            if (pre.next[high + 1] == null) {
                return getLast(node);
            }
            Node next = pre.next[high + 1];
            int left = getLen(pre, node, node.high);
            int right = getLen(node, next, node.high);
            if (left == right) {
                return node;
            }
            if (left > right) {
                return left(node, (left - right) / 2);
            } else {
                return right(node, (right - left) / 2);
            }
        }

        private int getLen(Node left, Node right, int high) {
            int step = 0;
            while (left != right) {
                left = left.next[high];
                step++;
            }
            return step;
        }

        private Node left(Node node, int step) {
            if (step == 0) {
                return node;
            }
            return left(node.pre[node.high], step - 1);
        }

        private Node right(Node node, int step) {
            if (step == 0) {
                return node;
            }
            return right(node.next[node.high], step - 1);
        }

        private Node getLast(Node node) {
            int high = node.high;
            while (node.next[high] != null) {
                node = node.next[high];
            }
            return node;
        }

        private Node getMoreHighPre(Node node) {
            int high = node.high;
            Node pre = node.pre[high];
            while (pre.high == high) {
                pre = pre.pre[high];
            }
            return pre;
        }

        private void setNext(Node pre, Node node) {
            int high = node.high;
            if (pre.next[high] == null) {
                pre.next[high] = node;
                node.pre[high] = pre;
            } else {
                Node next = pre.next[high];
                pre.next[high] = node;
                node.pre[high] = pre;
                node.next[high] = next;
                next.pre[high] = node;
            }
        }

        private void show() {
            System.out.println("总数"+i+"为出现越界");
            System.out.println("0级，并设置k");
            head.k = 0;
            int k = 0;
            Node node = head;
            while (node != null) {
                node.k = k++;
                node = node.next[0];
            }
            for (int i = 3; i < max; i++) {
                System.out.println(i + "级间隔：");
                node = head;
                Node next = node.next[i];
                while (next != null) {
                    System.out.print(next.k - node.k + ",");
                    node = next;
                    next = node.next[i];
                }
                System.out.println();
            }
        }

        @Override
        public String toString() {
            String s = "";
            Node node = head;
            while (node != null) {
                s += node.value + ",";
                node = node.next[0];
            }
            return s;
        }
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/386621.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于Canal的数据同步

基于Canal的数据同步

基于Canal的数据同步 一、 系统结构 该数据同步系统由Spring Boot和Canal共同组成。 Spring Boot 是一个流行的 Java Web 框架&#xff0c;而 Canal 则是阿里巴巴开源的 MySQL 数据库的数据变更监听框架。结合 Spring Boot 和 Canal&#xff0c;可以实现 MySQL 数据库的实时数…
阅读更多...
ASGCN之图卷积网络(GCN)

ASGCN之图卷积网络(GCN)

文章目录前言1. 理论部分1.1 为什么会出现图卷积网络&#xff1f;1.2 图卷积网络的推导过程1.3 图卷积网络的公式2. 代码实现参考资料前言 本文从使用图卷积网络的目的出发&#xff0c;先对图卷积网络的来源与公式做简要介绍&#xff0c;之后通过一个例子来代码实现图卷积网络…
阅读更多...
Linux命令行安装Oracle19c教程和踩坑经验

Linux命令行安装Oracle19c教程和踩坑经验

安装 下载 从 Oracle官方下载地址 需要的版本&#xff0c;本次安装是在Linux上使用yum安装&#xff0c;因此下载的是RPM。另外&#xff0c;需要说明的是&#xff0c;Oracle加了锁的下载需要登录用户才能安装&#xff0c;而用户是可以免费注册的&#xff0c;这里不做过多说明。 …
阅读更多...
最新使用nvm控制node版本步骤

最新使用nvm控制node版本步骤

一、完全卸载已经安装的node、和环境变量 ①、打开控制面板的应用与功能&#xff0c;搜索node&#xff0c;点击卸载 ②、打开环境变量&#xff0c;将node相关的所有配置清除 ③、打开命令行工具&#xff0c;输入node-v&#xff0c;没有版本号则卸载成功 二、下载nvm安装包 ①…
阅读更多...
SBUS的协议详解

SBUS的协议详解

SBUS 1.串口配置&#xff1a; 100k波特率&#xff0c; 8位数据位&#xff08;在stm32中要选择9位&#xff09;&#xff0c; 偶校验&#xff08;EVEN), 2位停止位&#xff0c; 无控流&#xff0c;25个字节&#xff0c; 2.协议格式&#xff1a; [startbyte] [data1][data2]……
阅读更多...
单月涨粉超600w，直播销售额破5亿，2月的黑马都是谁？

单月涨粉超600w，直播销售额破5亿，2月的黑马都是谁？

2月的抖音&#xff0c;黑马多多&#xff0c;处处有爆点。有直播间热度不减&#xff0c;在带货领域持续位列前茅&#xff1b;有达人通过“抓马式”连麦直播&#xff0c;涨粉657w&#xff1b;有0.01元的低价商品&#xff0c;一天热卖超1000w个。那么&#xff0c;2月有哪些主播表现…
阅读更多...
微服务实战03-注册数据服务

微服务实战03-注册数据服务

EurekaServer &#xff0c;它扮演的角色是注册中心&#xff0c;用于注册各种微服务&#xff0c;以便于其他微服务找到和访问。有了EurekaServer&#xff0c;还需要一些微服务&#xff0c;注册到EurekaServer上去。 这一节&#xff0c;我们来写一个注册微服务。为了简单起见&am…
阅读更多...
【同步工具类:Phaser】

【同步工具类:Phaser】

同步工具类:Phaser介绍特性动态调整线程个数层次Phaser源码分析state 变量解析构造函数对state变量赋值阻塞方法arrive()awaitAdvance()业务场景实现CountDownLatch功能代码测试结果实现 CyclicBarrier功能代码展示测试结果总结介绍 一个可重复使用的同步屏障&#xff0c;功能…
阅读更多...
26- AlexNet和VGG模型分析 (TensorFlow系列) (深度学习)

26- AlexNet和VGG模型分析 (TensorFlow系列) (深度学习)

知识要点 AlexNet 是2012年ISLVRC 2012竞赛的冠军网络。 VGG 在2014年由牛津大学著名研究组 VGG 提出。 一 AlexNet详解 1.1 Alexnet简介 AlexNet 是2012年ISLVRC 2012&#xff08;ImageNet Large Scale Visual Recognition Challenge&#xff09;竞赛的冠军网络&#xff0…
阅读更多...
paddle推理部署（cpu)

paddle推理部署（cpu)

我没按照官方文档去做&#xff0c;吐槽一下&#xff0c;官方文档有点混乱。。一、概述总结起来&#xff0c;就是用c示例代码&#xff0c;用一个模型做推理。二、示例代码下载https://www.paddlepaddle.org.cn/paddle/paddleinferencehttps://github.com/PaddlePaddle/Paddle-In…
阅读更多...
Clion连接Docker，使用HElib库

Clion连接Docker，使用HElib库

文章目录需求Clion连接服务器内的DockerDockerCLionDocker内配置HElib库参考需求 HElib库是用C编写的同态加密开源库&#xff0c;一般在Linux下使用为了不混淆生产环境&#xff0c;使用Docker搭建HElib运行环境本地在Windows下开发&#xff0c;使用的IDE为Clion&#xff0c;本…
阅读更多...
动态规划：leetcode 121. 买卖股票的最佳时机、122. 买卖股票的最佳时机II

动态规划：leetcode 121. 买卖股票的最佳时机、122. 买卖股票的最佳时机II

leetcode 121. 买卖股票的最佳时机leetcode 122.买卖股票的最佳时机IIleetcode 121. 买卖股票的最佳时机给定一个数组 prices &#xff0c;它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票&#xff0c;并选择在 未来的某一个不同的日…
阅读更多...
node版本管理工具nvm

node版本管理工具nvm

1.标题卸载nvm和node.js 系统变量中删除nvm添加变量&#xff1a;NVM_HOME和NVM_SYMLINK环境变量中 path&#xff1a;删除nvm自动添加的变量 Path %NVM_HOME%;%NVM_SYMLINK%删除自身安装node环境&#xff0c;参考图一图二 图一 图二 2.安装nvm nvm-window下载------https:/…
阅读更多...
ES window 系统环境下连接问题

ES window 系统环境下连接问题

环境问题&#xff1a;&#xff08;我采用的版本是 elasticsearch-7.9.3&#xff09;注意 开始修正之前的配置&#xff1a;前提&#xff1a;elasticsearch.yml增加或者修正一下配置&#xff1a;xpack.security.enabled: truexpack.license.self_generated.type: basicxpack.secu…
阅读更多...
对象实例化【JVM】

对象实例化【JVM】

JVM对象实例化简介/背景一、创建对象的方式1. new2. Class对象的newInstance方法3. Construstor对象的newInstance(xx)方法4. 使用clone方法二、创建对象的步骤1. 判断对象是否已经加载、链接、初始化2. 为对象分配内存3. 处理并发安全问题4. 初始化分配到的空间5. 设置对象的对…
阅读更多...
Tech Lead如何引导团队成员解决问题？

Tech Lead如何引导团队成员解决问题？

作为一个开发团队的Tech Lead&#xff0c;当团队成员向你寻求帮助时&#xff0c;你有没有说过下面这些话&#xff1f; 你别管了&#xff0c;我来解决这个问题你只要。。。就行了你先做其他的吧&#xff0c;我研究一下&#xff0c;然后告诉你怎么做 当我们说这些话时&#xff…
阅读更多...
腾讯免费企业邮箱迁移记录

腾讯免费企业邮箱迁移记录

本文记录在重新申请腾讯企业邮箱的过程。 背景 很多年前&#xff0c;将域名latelee.org 迁移到了阿里云&#xff0c;当时因政策原因无法实名&#xff0c;但能使用。去年3月&#xff0c;阿里云提示无法续费&#xff0c;紧急将其转到外面某服务&#xff0c;继续使用&#xff0c;…
阅读更多...
IP地址的工作原理

IP地址的工作原理

如果您想了解特定设备为何未按预期方式进行连接&#xff0c;或者想要排查网络无法正常工作的可能原因&#xff0c;它可以帮助您了解 IP 地址的工作原理。互联网协议的工作原理与任何其他语言相同&#xff0c;即使用设定的准则进行通信以传递信息。所有设备都使用此协议与其他连…
阅读更多...
jq获取同级或者下级的dom节点的操作

jq获取同级或者下级的dom节点的操作

1.使用find找到对应的class或者其他 var class_dom1 obj.find(.class名称);或者 find(span .class名称)2.使用添加背景颜色来确定当前的查找位置 class_dom1.css(background,red);3.通过parent来找到它的上级的dom节点 var parent_li_dom1 class_dom1.parent(li.parent_li…
阅读更多...
进阶指针——（2）

进阶指针——（2）

本次讲解重点&#xff1a; 6. 函数指针数组 7. 指向函数指针数组的指针 8. 回调函数 在前面我们已经讲解了进阶指针的一部分&#xff0c;我们回顾一下在进阶指针(1)我们学过的难点知识点&#xff1a; int my_strlen(const char* str) {return 0; }int main() {//指针数…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023