摘要

链表中环的入口结点_牛客题霸_牛客网

剑指 Offer II 022. 链表中环的入口节点

141. 环形链表

142. 环形链表 II

一、是否有环（快慢指针）

我们可以根据上述思路来解决本题。具体地，我们定义两个指针，一快一慢。慢指针每次只移动一步，而快指针每次移动两步。初始时，慢指针在位置 head，而快指针在位置 head.next。这样一来，如果在移动的过程中，快指针反过来追上慢指针，就说明该链表为环形链表。否则快指针将到达链表尾部，该链表不为环形链表。

public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) {
            return false;
        }
        ListNode slow = head;
        ListNode fast = head.next;
        while (slow != fast) {
            if (fast == null || fast.next == null) {
                return false;
            }
            slow = slow.next;
            fast = fast.next.next;
        }
        return true;
    }
}

复杂度分析

时间复杂度：O(N)，其中N是链表中的节点数。当链表中不存在环时，快指针将先于慢指针到达链表尾部，链表中每个节点至多被访问两次。当链表中存在环时，每一轮移动后，快慢指针的距离将减小一。而初始距离为环的长度，因此至多移动N轮。
空间复杂度：O(1)。我们只使用了两个指针的额外空间。

二、环的入口（快慢指针）

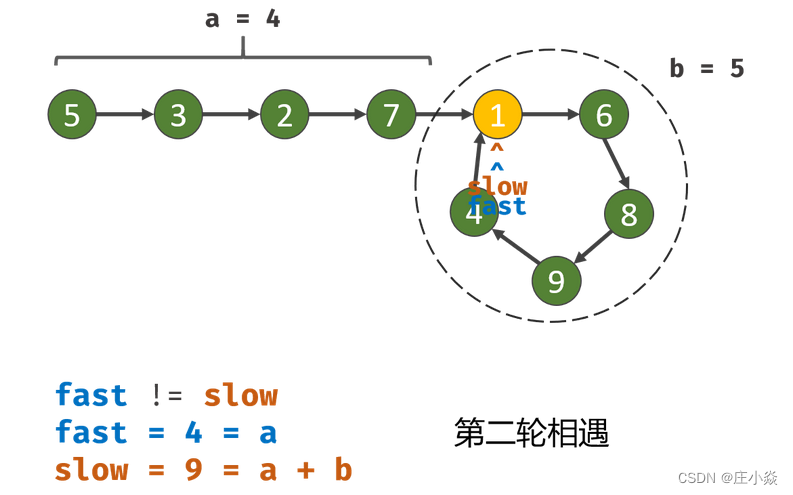
思路与算法：我们使用两个指针，fast与slow。它们起始都位于链表的头部。随后，slow指针每次向后移动一个位置，而fast指针向后移动两个位置。如果链表中存在环，则 fast指针最终将再次与slow 指针在环中相遇。

如下图所示，设链表中环外部分的长度为a。slowslow 指针进入环后，又走了b的距离与fast 相遇。此时，fast指针已经走完了环的n圈，因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc。

package Linklist;

/**
 * @Classname JZ23环的入口位置
 * @Description TODO
 * @Date 2023/3/3 21:30
 * @Created by xjl
 */
public class JZ23环的入口位置 {

    class ListNode {
        int val;
        ListNode next;

        ListNode(int x) {
            val = x;
            next = null;
        }
    }

    public ListNode detectCycle(ListNode head) {
        ListNode fast = head, slow = head;
        while (true) {
            if (fast == null || fast.next == null) {
                return null;
            }
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                break;
            }
        }
        fast = head;
        while (slow != fast) {
            slow = slow.next;
            fast = fast.next;
        }
        return fast;
    }
}

复杂度分析：