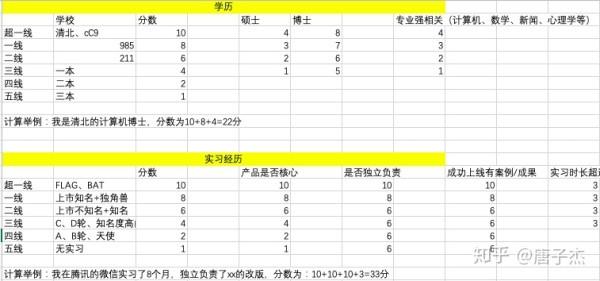
目录
函数极限的定义:
数列的极限和函数极限
定理1:
自变量趋向有限制时,函数的极限
左右极限:
定理:
需要分左右极限求极限的三种问题:
例题:
例2:
极限性质:
保号性:
函数的保号性
例题:
极限值与无穷小值
夹逼准则:
单调有界准则:
例题:
例题:
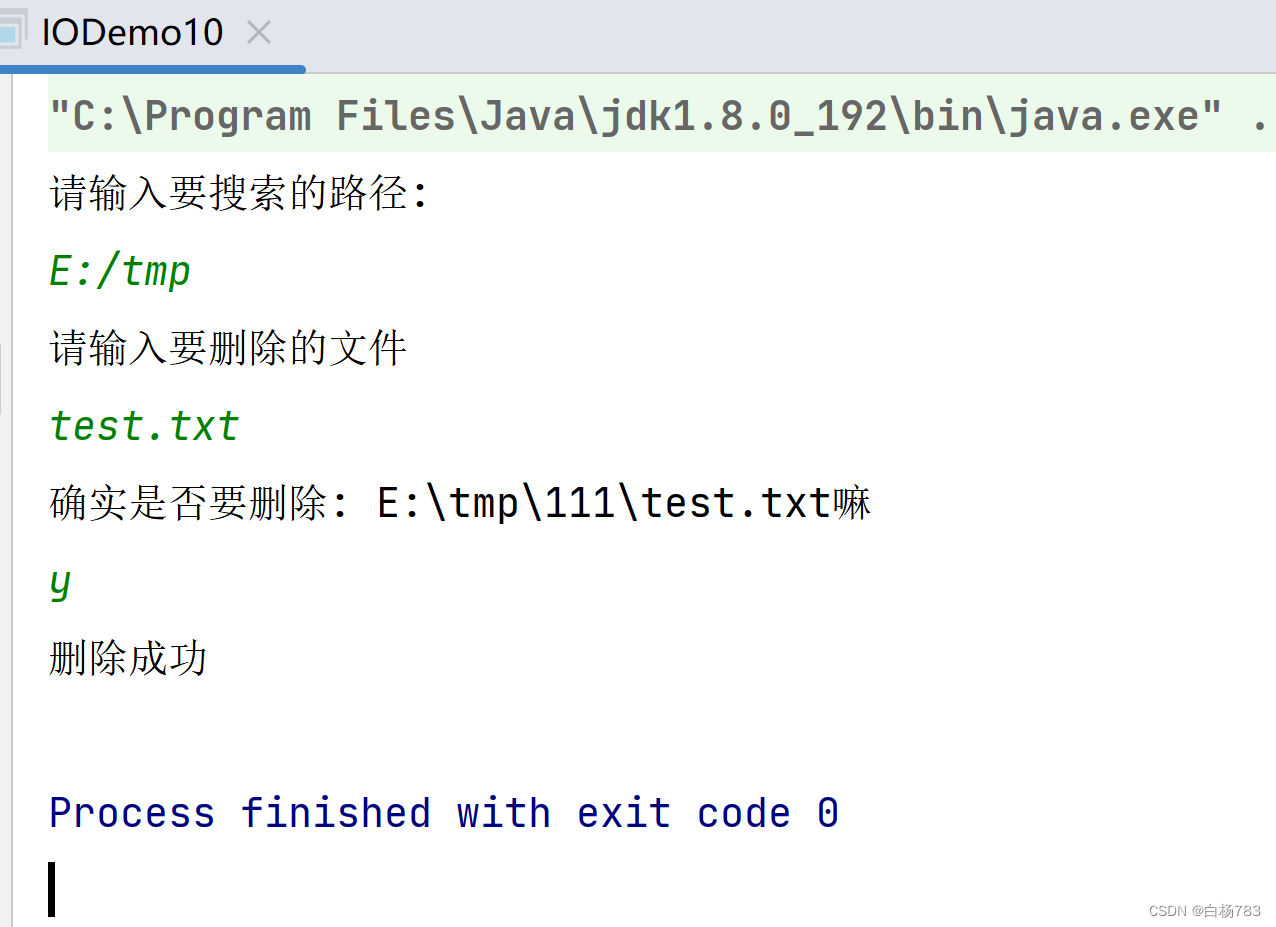
编辑
例题:
无穷小量:
无穷小的性质:
无穷大量:
无穷大量的比较
对于数列的无穷大:
无穷大量的定理:
无穷大量与无界变量的关系:
无穷大量与无穷小量之间的关系:
函数极限的定义:

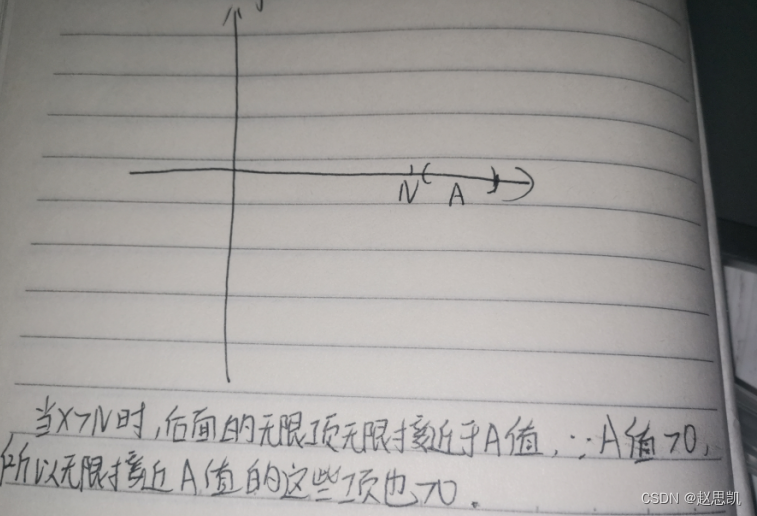
最浅显的理解就是当自变量x趋向于正无穷时,我们的函数值无限接近于A。
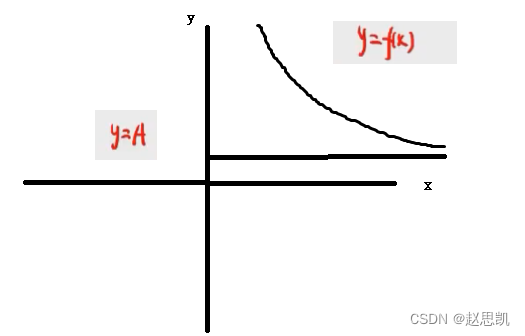
如图所示,当x无限增大时,f(x)的图像无限接近于直线y=A 。

如何理解这部分呢?

答:

理解:


这里的理解:


总体的理解,一句话。

几何理解:

数列的极限和函数极限

这是我们上节课学习的数列的极限,数列的极限其实就是一个正标函数:
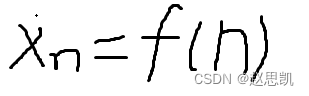
与其他函数的不同点在于正标函数的自变量只能够取正整数。
那么数列的极限和函数的极限之间的关系是怎样的呢?

我们的函数的极限可以推出数列的极限,但是数列的极限无法推出函数的极限。
原因是我们的函数的自变量可以是任意的实数,而我们的数列的自变量只能是正整数。
由一般的可以推出特殊,但是由特殊推不出一般。
例如:
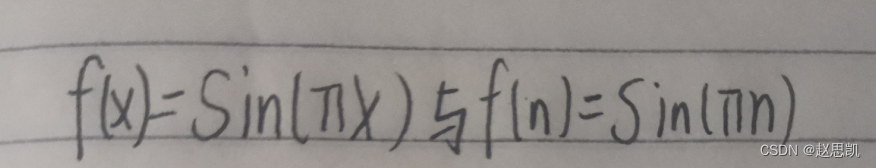
对于f(x),我们的自变量x可以为任意实数,所以我们的f(x)是在[-1,1]之间波动的,所以f(x)没有极限,因为f(n)的自变量为正整数,所以f(n)始终等于0,所以数列f(n)的极限值为0.
所以当我们想要求出数列的极限时,因为函数的极限可以推导出数列的极限,所以我们可以把数列的极限转换为函数的极限求。
意义是什么呢?
假如我们想要使用洛必达法则求极限,我们首先要要求数列是可导的,但是数列的自变量是只有正整数,所以数列不能使用洛必达法则,所以我们可以把数列转换为函数,调用洛必达法则求极限。


不再赘述。

反之不成立,我们需要保证两个单侧的极限值相等,才成立。
定理1:
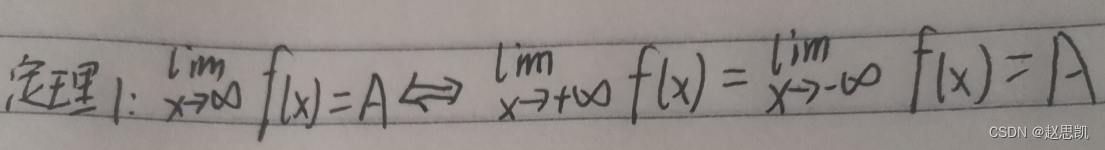
例题:
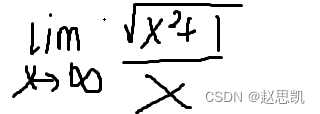
极限值是多少?
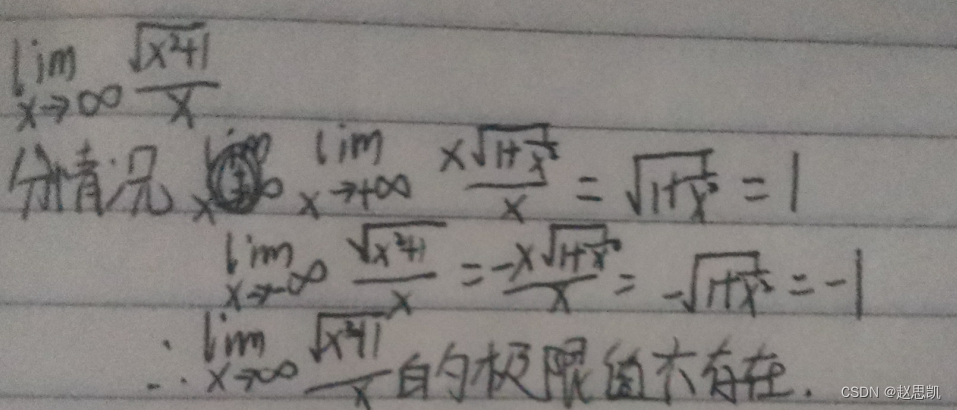
对于数列的极限呢?
自变量趋向有限制时,函数的极限

我们对定义进行理解:
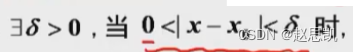

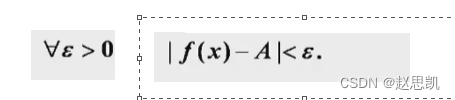
我们对这里进行理解:

![]() 一句话理解:
一句话理解:

几何意义:
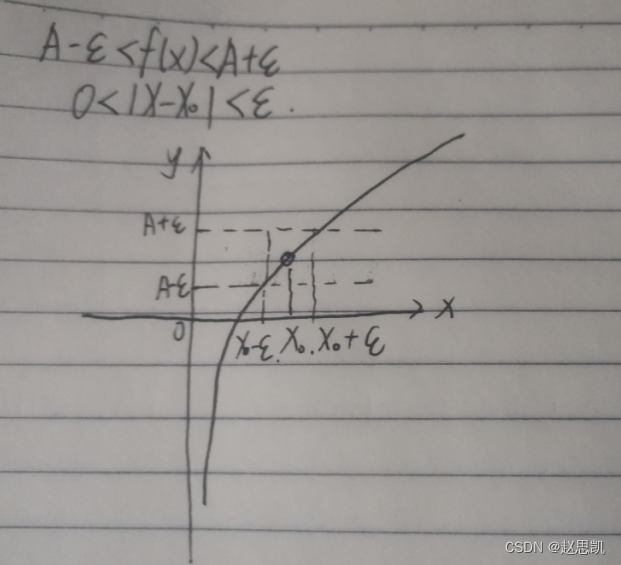
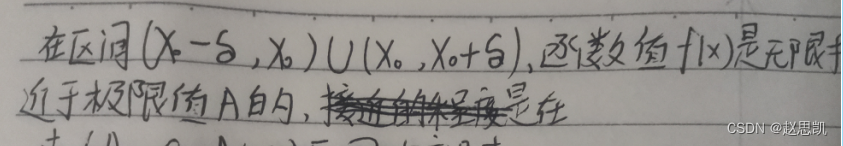
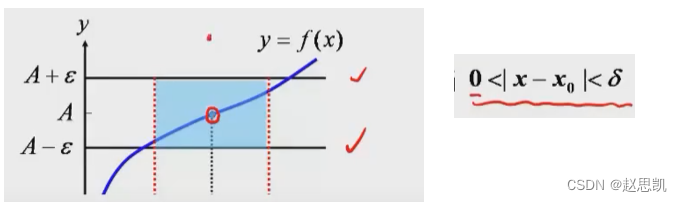
所以x不等于x0,但是x不能等于x0
如图像所示,x趋近于x0,但是x不能等于x0,f(x)趋近于A,f(x)可以等于A。
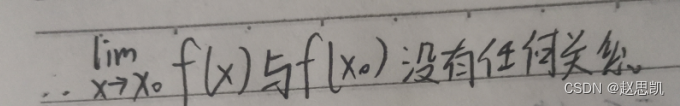

举例:
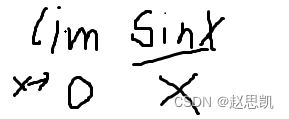
这个函数在x=0时是没有定义的,所以f(0)和极限是没有任何关系的。
我们再举一个例子:
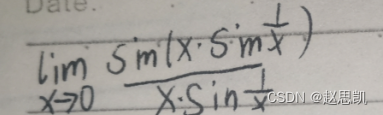
这个极限值是多少?
答:

这样写对吗?
这种写法是错误的。

所以极限是不存在的。
所以,许多教材写的这些的定理也是错误的。
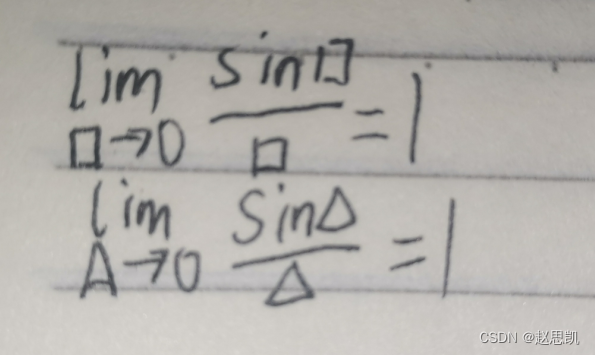
三角和方框代表的是函数,所以我们是要把这些函数当作自变量来求极限,所以我们要保证这些函数的函数值在自变量趋于0时不等于0,否则就是极限不存在。
所以我们要保证三角或者方框趋近于0且不等于0.
第二种理解方法:

左右极限:
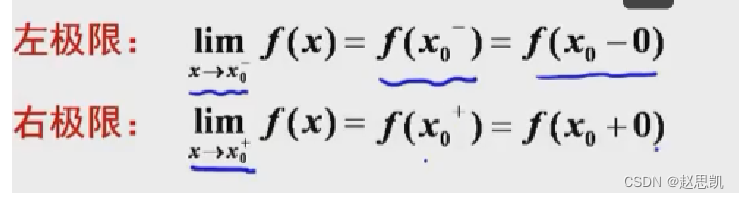
我们画一个简图帮助理解:

定理:

当极限存在并且等于A时可以推出左右极限都存在并且等于A,反之也成立。
需要分左右极限求极限的三种问题:

第一种见的很多,不需要赘述。
例如:

许多人直接说极限是无穷大,是错误的,我们要分情况进行讨论。
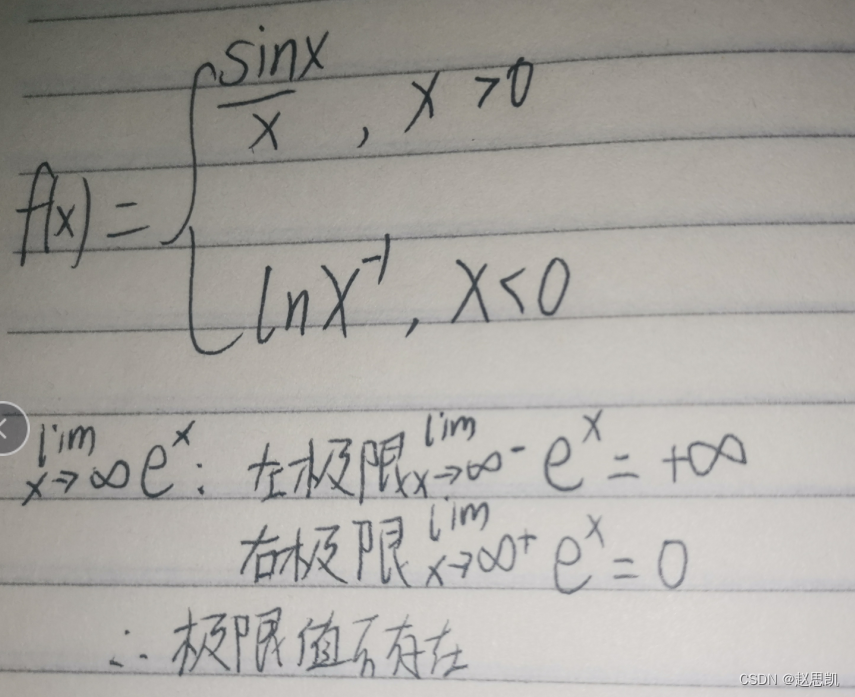
例如:

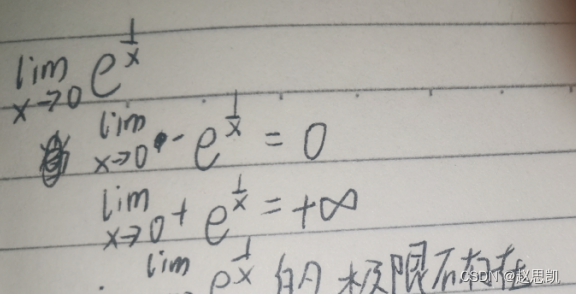
例如:

我们画出arctanx的图像:
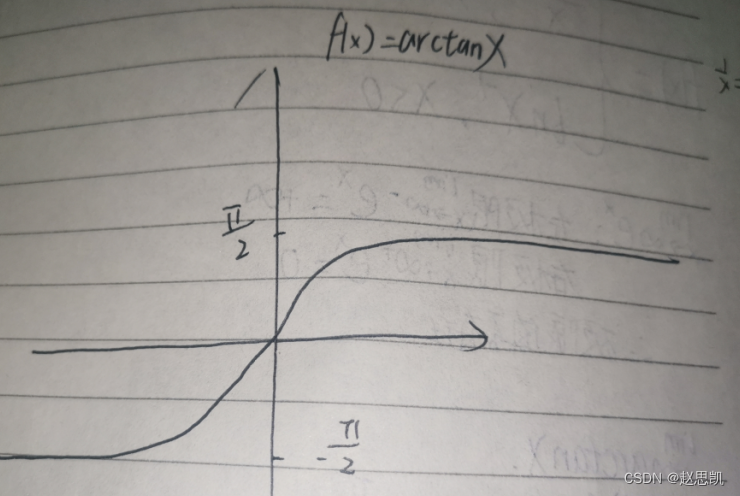

例如:

例题:


例2:
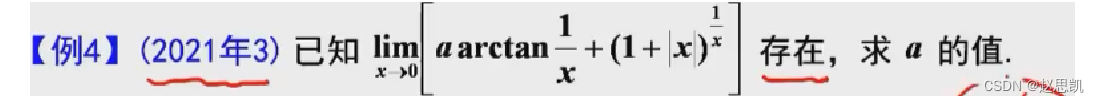
极限性质:

数列收敛就是数列有极限的意思,当数列收敛时,数列一定有界。
反之成立吗,我们举一个反例:
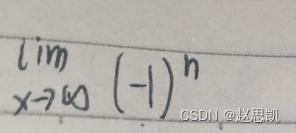
我们的数列是有界的,但是我们的数列是在-1和1之间来回跳转的,所以我们的数列是没有极限。
证明:有界数列不一定收敛。
为什么收敛数列必有界?
答:

那么对于函数来说,有这些性质吗?


这就是局部有界的意思。
反之成立吗?
不成立,我们举出反例。

所以,收敛函数可以推出函数在某去心领域内有界,反之不成立。
保号性:

我们进行说明:
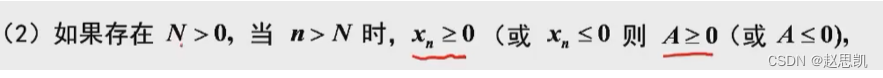
参考上面的证明。
我们能不能把定理这样修改:

不能,我们对定理1举反例:

我们对定理2举反例:
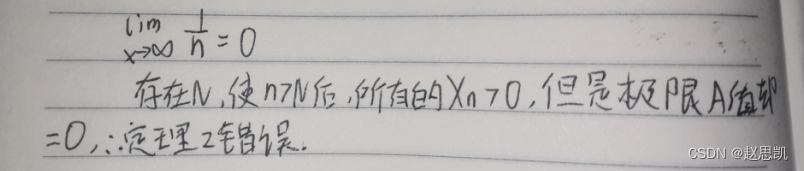
函数的保号性

如果极限值A>0,那么存在一个去心领域,在去心领域内部,f(x)始终大于0.
如果存在一个去心领域,在去心领域内部f(x)大于等于0,那么极限值A大于等于0.
例题:



极限值与无穷小值
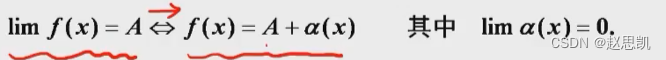
f(x)的极限为A时的充分必要条件是f(x)=极限值加一个无穷小值。
我们进行证明:

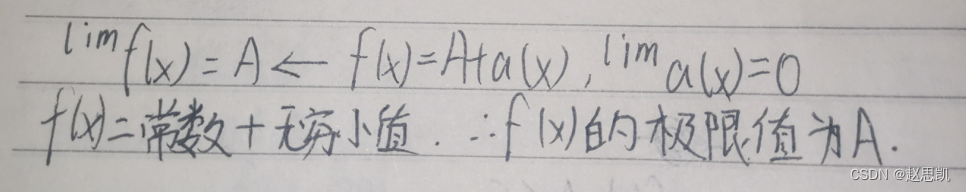
夹逼准则:
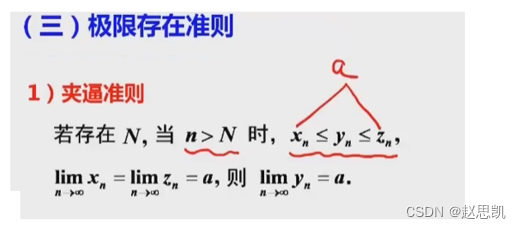
我们把数列极限的定义和夹逼准则放在一起:

我们进行画图解释:
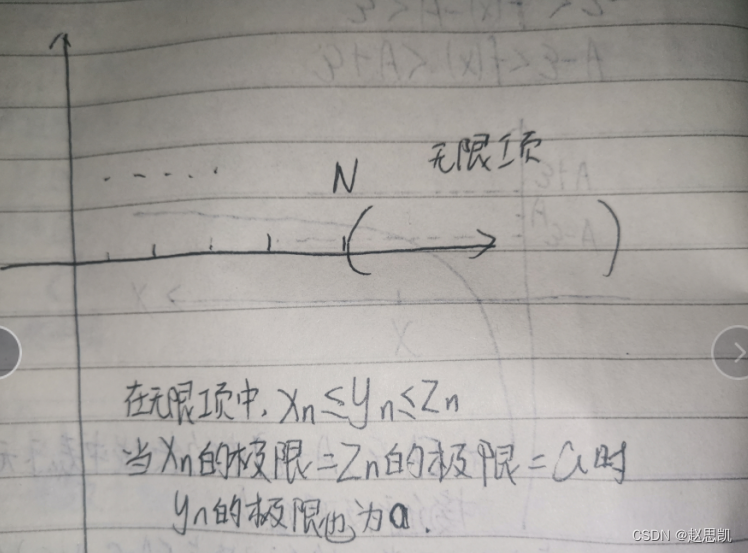
单调有界准则:

单调有界数列必定有极限,有界的意思是既有上界又有下界,并且上界和下界的值相等,数列还是单调的,所以数列一定有极限。

因为我们的第一项就是下界,所以上界下界都控制了,所有就有极限。
第二个不再赘述。
例题:
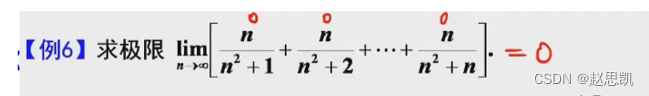
结果对吗?

例题:

例题:


第二种解法:

无穷小量:

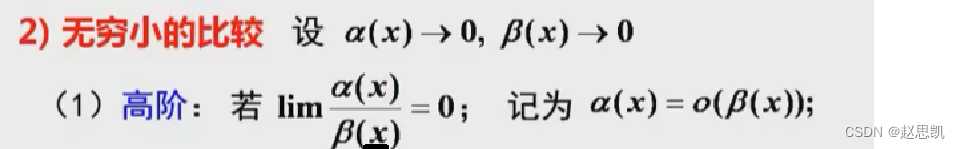
无穷小之间的比较比较的是趋近于0的速度,
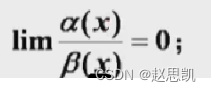
表示a(x)趋近于0的速度大于B(x)
表示a(x)是B(x)的高阶无穷小。

无穷小的性质:

无限个无穷小的和还是不是无穷小呢?
答:无限个无穷小的和不一定是无穷小,例如:
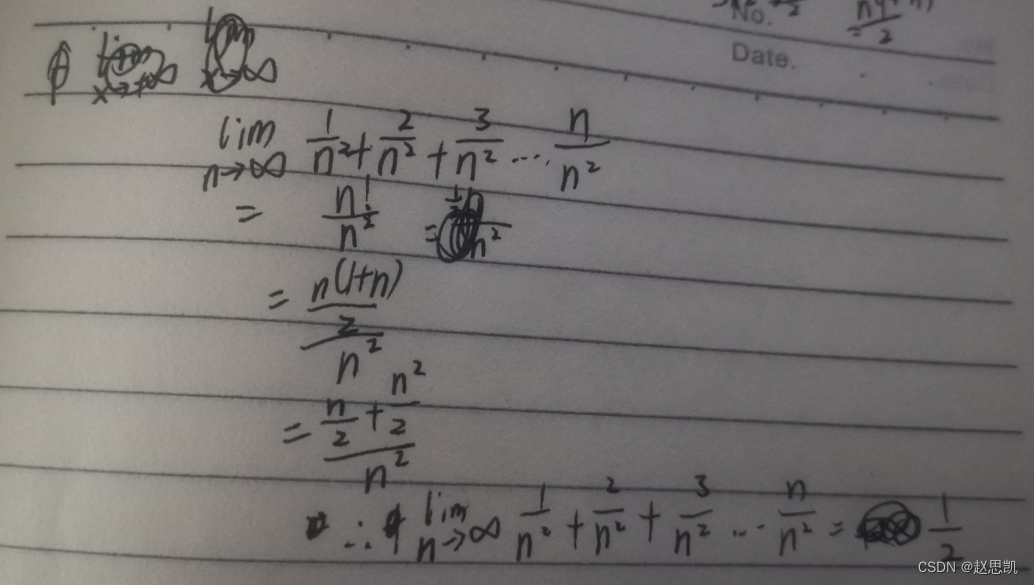

那么这道题目呢?
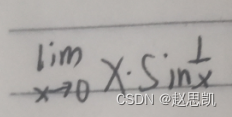
第一种解法:

这种写法是标准的错误,错误原因在这里:

最正确的写法:

无穷大量:


趋向于无穷包括正无穷和负无穷。
对无穷大量的数学理解:
![]()
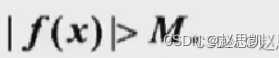
M是任意值,而函数值的绝对值比任意值都大,那么函数值就是正无穷或者负无穷,这个是结论。

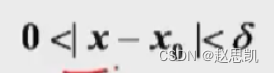

无穷大量的比较

后面的比前面的趋向于无穷大的速度更快。
后面一个闭上前面一个的极限是无穷大。
前面一个闭上后面一个的极限是无穷小。
例如:
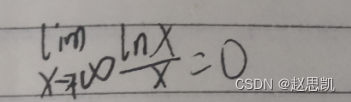
对于数列的无穷大:
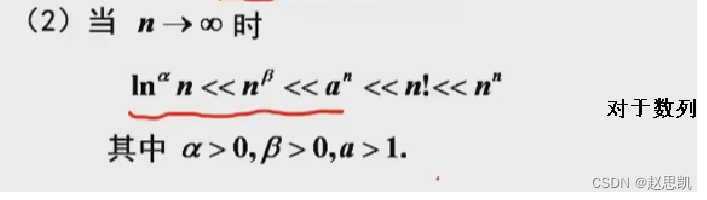
例题:


无穷大量的定理:

![]()
无穷大*有界的结果是无穷大吗?
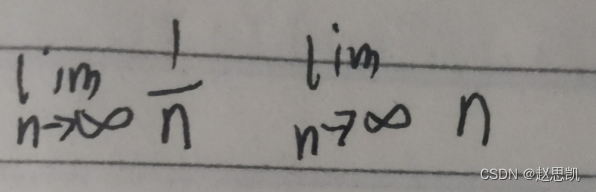
对于数列,第一个是有界,第二个是无穷大,但是相乘的极限值为1.
无穷大量与无界变量的关系:

无穷大量是存在一个N,在N之后的所有项对应的Xn都为无穷大。
误解变量是存在一项,使Xn为无穷大。
无穷大量是都很大,而无界变量是有很大。
所以由一般可以推导出特殊,而由特殊无法推导到一般。

举一个例子:
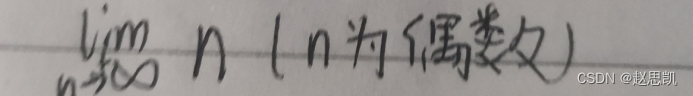
这是一个无界变量,但是无法推导出他是无穷大量。

例题:

上面的一段的极限为无穷,而下面一段的极限是0,所以Xn是无界变量。
无穷大量与无穷小量之间的关系: