在这里插入图片描述

👑专栏内容：数据结构
⛪个人主页：子夜的星的主页
💕座右铭：日拱一卒，功不唐捐

文章目录

一、前言
二、链表
- 1、定义
- 2、单链表
- - Ⅰ、新建一个节点
  - Ⅱ、内存泄漏
  - Ⅲ、插入一个节点
  - Ⅳ、销毁所有节点
  - Ⅴ、反转一个链表
- 3、双向链表
- 4、循环链表
- - Ⅰ、单向循环链表
  - Ⅱ、双向循环链表
  - Ⅲ、循环链表总结
  - Ⅳ、一些OJ题
  - - ①、环形链表
    - ②、快乐数
三、总结
- 1、区别
- 2、优点
- 3、缺点

一、前言

前面介绍了线性结构中的顺序表，顺序表的随机访问速度非常快，但是它最大的缺点就是插入和删除的时候要移动大量元素。而链表这一数据结构就能完美的解决这一问题。那么链表是如何解决的呢？

在这里插入图片描述

二、链表

1、定义

链表是一种链式存取的数据结构，用一组地址任意的存储单元存放线性表中的数据元素。链表中的数据是以结点来表示的，每个结点的构成：元素(数据元素的映象) + 指针(指示后继元素存储位置)，元素就是存储数据的存储单元，指针就是连接每个结点的地址数据。

由于是分散存储，为了能够体现出数据元素之间的逻辑关系，每个数据元素在存储的同时，要配备一个指针，用于指向它的直接后继元素，即每一个数据元素都指向下一个数据元素（最后一个指向NULL(空)）。
链表中每个元素本身由两部分组成：
● 数据域：存放数据。
● 指针域：存放指向后继结点的地址；
链表的第一个结点被称为：头节点

正因为如此，我们只需要记住链表中的头节点就行，顺着头节点这个藤，逐渐的可以找到链表中其他所有的节点。

在这里插入图片描述

typedef struct LinkNode {
		int data;//数据域
		struct LinkNode *next;//指针域
}Node;

在这里插入图片描述

2、单链表

单链表，顾名思义。链表指向的只有一个方向。

在这里插入图片描述

Ⅰ、新建一个节点

Node *getNewNode(int val) {
    Node *p = (Node *)malloc(sizeof(Node)); //（1）
    p->data = val;  	//（2）
    p->next = NULL;	    //（3）
    return p;			//（4）
}

（1）开辟一个空间用来存储新的节点
（2）将新建节点的数据放入数据域中
（3）将新节点的指针域置为 NULL
（4）返回新建的节点

Ⅱ、内存泄漏

在进行插入操作之前，先搞明白一个概念，那就是内存泄露。

内存泄漏：由于疏忽或错误造成程序未能释放已经不再使用的内存。
在这里插入图片描述
就拿链表来看，我们知道的只有程序内部的头地址，依据头地址中存储的下一个链表的地址来找到下一个链表，从而，拔出萝卜带出泥，找到所有的链表。但是试想一下，加入我们在操作的过程中不小心把其中一个链表的地址弄丢了呢？
在这里插入图片描述
就像这样，因为错误的插入，导致弄丢了②和③的地址，导致②和③这两个链表数据在内存内部中无法被找到，也无法被清理。

在这里插入图片描述

Ⅲ、插入一个节点

如下图，我们想在①和②中间插入④，或者这样说，将④插入链表的2号位置，应该怎么操作呢？

在这里插入图片描述

首先当然应该让p指针走向2号位置的前一个位置，也就是1号位置处。

然后，很多人就会犯这样的错误

p->next = node; //（1）
node ->next = p->next ; //（2）

这样看似没有问题，但是仔细看一下，在执行完（1）后，p->next已经不是②的地址了。你再执行（2）其实是将node->next指向node自己。

在这里插入图片描述
这样就造成了前文说的内存泄漏，也就是说②和③从此就会一直呆在你的内存里面，你调用不了也销毁不了这两个链表。所以，我们插入结点时，一定要注意操作的顺序，要先将结点 node 的 next 指针指向下一个节点地址，再把结点 ① 的 next指针指向结点node，这样才不会丢失指针，导致内存泄漏。所以，对于刚刚的插入代码，我们只需要把第 1 行和第 2 行代码的顺序颠倒一下就可以了。

Node *insert(Node *head,int pos ,int val) //（1）
{
	if(pos ==0) //（2）
	{
		Node *p = getNewNode (val);
		p->next = head;
		return p;
	}
	Node *p = head; 
	for(int i =1;i<pos;i++) 
		p = p->next;      //（3）
	Node *node = getNewNode(val); //（4）
	node ->next = p->next ;  //（5）
	p->next = node;  //（6）
	return head;
}

（1）pos是要插入的位置
（2）pos等于0就是放在头地址处
（3）让p指针走向待插入位置的前一个位置
（4）创建一个要插入的节点
（5）先让新建节点的指针指向待原本插入位置的节点地址
（6）让待前一个位置的指针指向新建要插入的节点

上面的代码自然能够很好的完成插入操作，但是这样代码写起来就会很繁琐，而且也容易出错。如何来更好的解决这个问题呢？仔细看下上面的插入操作，代码较长的原因，主要是怕插入的位置是头位置。所以我们要对这一情况进行特殊处理。但是，如果我们建立一个虚拟的头节点呢？这样不就可以解决找个问题了吗？
在这里插入图片描述

Node *insert(Node *head,int pos ,int val)
{
	Node new_head,*p = &new_head;  //（1）
	Node *node = getNewNode(val); 
	new_head.next = head //（2）
	for(int i=0;i<pos;i++) p= p->next; //（3）
	node->next = p->next; //（3）
	p->next = node;//（3）
	return new_head.next; //（4）
}

（1）新建一个虚拟的头节点
（2）让虚拟头节点的指针指向真实的头地址
（3）进行插入操作
（4）返回虚拟头节点的指向的地址，也就是真实的头地址

在这里插入图片描述

Ⅳ、销毁所有节点

注意：销毁所有的节点不能直接free(head)，因为你如果直接释放了头节点，那么你根本找不到后面其他节点。
所以，应该新建一个指针，指向要销毁节点的下一个节点，再不断的更新这个指针指向的位置，依次销毁所有节点。切记，万万不可只销毁头节点。

void clear(Node *head) {
    if (head == NULL) return ;
    for (Node *p = head, *q; p; p = q) //（1）
    {
        q = p->next;	//（1）
        free(p);	    //（2）
    }
    return ;
}

（1）循环不断更新p指针指向的节点位置
（2）销毁节点

Ⅴ、反转一个链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

在这里插入图片描述
常规解法：

 struct ListNode* reverseList(struct ListNode* head) {
    struct ListNode new_head,*p = head,*q;
	new_head.next = NULL;
	while(p){
			q = p->next;
			p->next = new_head.next;
            new_head.next = p;
			p=q;
	}
	return new_head.next;
    }

递归解法：

 struct ListNode* reverseList(struct ListNode* head) {
     if(head == NULL||head->next == NULL)
            return head;
        struct ListNode *tail = head->next;
        struct ListNode *new_head = reverseList(head->next);
        head->next = tail->next;
        tail->next = head ;
        return new_head;
    }

3、双向链表

双向链表是在单链表的每个结点中，再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域，一个指向直接后继，另一个指向直接前驱。

typedef struct DoubleLinkNode
{
		int data;//数据域
		struct DoubleLinkNode *pre; //指向前一个的地址
		struct DoubleLinkNode *next;//指向后一个的地址
}DulNode;

在这里插入图片描述
双向链表的优点是可以找到前驱和后继，可进可退。
但是，这同时也让增加和删除变得复杂，需要多分配一个指针存储空间。

4、循环链表

循环链表是指在链表的基础上，表的最后一个元素指向链表头结点，不再是为空。
那么头指针指向那个节点呢？
在循环链表中，头指针指向的是循环链表的最后一个节点。
因为在循环链表中，最后一个节点即类似于前面提到的虚拟头节点，也是一个真实的节点。

Ⅰ、单向循环链表

从一个结点出发可以找到其他任何一个结点。
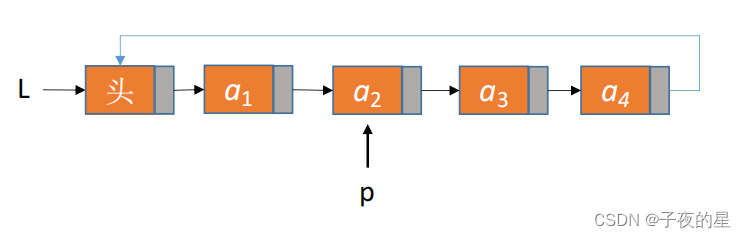
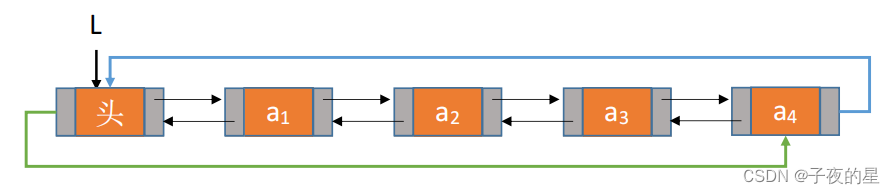
在这里插入图片描述

Ⅱ、双向循环链表

表头结点的 pre指向表尾结点；表尾结点的next指向头结点。
双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构，都是带头双向循环链表。另外这个结构虽然结构复杂，但是使用代码实现以后会发现结构会带来很多优势，实现反而简单了。
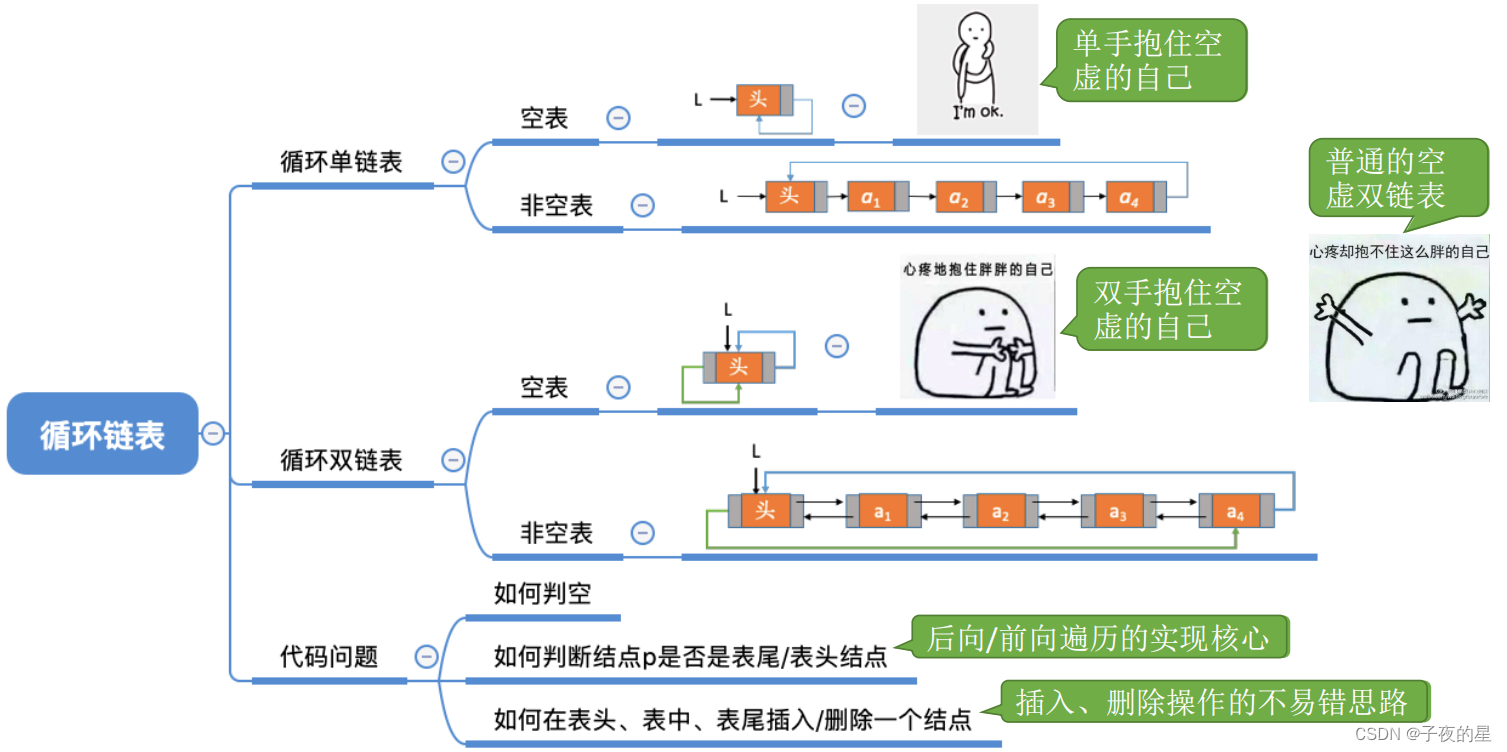
在这里插入图片描述

Ⅲ、循环链表总结

在这里插入图片描述

Ⅳ、一些OJ题

①、环形链表

力扣-141：环形链表
给你一个链表的头节点 head ，判断链表中是否有环。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。
如果链表中存在环，则返回 true 否则，返回false
在这里插入图片描述
使用快慢指针法，分别定义两个指针，从头结点出发，快的指针每次移动两个节点，慢的指针每次移动一个节点，如果快慢指针指针在途中相遇，说明这个链表有环。

bool hasCycle(struct ListNode *head) {
    struct ListNode *p = head,*q=head;
        while(q&&q->next)
        {
            p = p->next;
            q = q->next->next;
            if(p==q)
                return true;
        }
        return false;
}

②、快乐数

力扣-202：快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为：
对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。
如果这个过程结果为 1，那么这个数就是快乐数。
如果 n 是快乐数就返回 true；不是，则返回 false。

在这里插入图片描述
可以转化为上面的找环问题。

 int getNext(int x) {
        int d, y = 0;
        while (x) {
            d = x % 10;
            y += d * d;
            x /= 10;
        }
        return y;
    }
    bool isHappy(int n) {
        int p = n, q = n;
        while (q != 1) {
            p = getNext(p);
            q = getNext(getNext(q));
            if (p == q && p != 1) return false;
        }
        return true;
    }

三、总结

1、区别

不同点	顺序表	链表
存储空间上	物理上一定连续	逻辑上连续，但物理上不一定连续
随机访问	支持：O(1)	不支持：O(N)
任意位置插入或者删除元素	可能需要搬移元素，效率低O(N)	只需修改指针指向
插入	动态顺序表，空间不够时需要扩容	没有容量的概念
应用场景	元素高效存储+频繁访问	任意位置插入和删除频繁
缓存利用率	高	低

2、优点

①.链表是一个动态数据结构，无需给出链表的初始大小。
②.任意位置插入删除时间复杂度为O(1)。
与数组不同，在插入或删除元素后，我们不必移动元素。在链表中，我们只需要更新节点的下一个指针中存在的地址即可。
③.由于链表的大小可以在运行时增加或减小，因此不会浪费内存。

3、缺点

①.存储密度小，因为每个数据元素，都需要额外存储一个指向下一元素的指针（双链表则需要两个指针）。
②.要访问特定元素，只能从链表头开始，遍历到该元素，时间复杂度为 O ( n) 在特定的数据元素之后插入或删除元素，不涉及到其他元素的移动，因此时间复杂度为 O ( 1) 。双链表还允许在特定的数据元素之前插入或删除元素。
③.存储空间不连续，数据元素之间使用指针相连，每个数据元素只能访问周围的一个元素（根据单链表还是双链表有所不同）。

在这里插入图片描述