【论文阅读】Attributed Graph Clustering with Dual Redundancy Reduction（AGC-DRR）

1. 来源

Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence (IJCAI-22)
论文链接：Attributed Graph Clustering with Dual Redundancy Reduction
论文code：对应code

2. 动机

属性图聚类是图数据探索的一种基本而又必要的方法。最近在图对比学习方面的努力已经取得了令人印象深刻的聚类性能。然而，作者观察到：

• 普遍采用的InfoMax操作倾向于捕获冗余信息，限制了下游集群性能。

为此，作者开发了一种新的方法，称为双冗余减少的属性图聚类（AGC-DRR），以减少输入空间和潜在特征空间中的信息冗余。特别地，

• 为了减少输入空间的冗余，引入了一种对抗性学习机制来自适应地学习冗余的掉边矩阵，以确保比较样本对的多样性。
• 为了减少潜在空间中的冗余度，作者强制使用交叉增强样本嵌入的相关矩阵来近似一个单位矩阵。
• 基于此，学习到的网络在区分不同样本的同时，必须对扰动具有鲁棒性。
• 大量的实验已经证明，AGC-DRR在大多数基准测试上优于最先进的聚类方法。

3. 模型框架

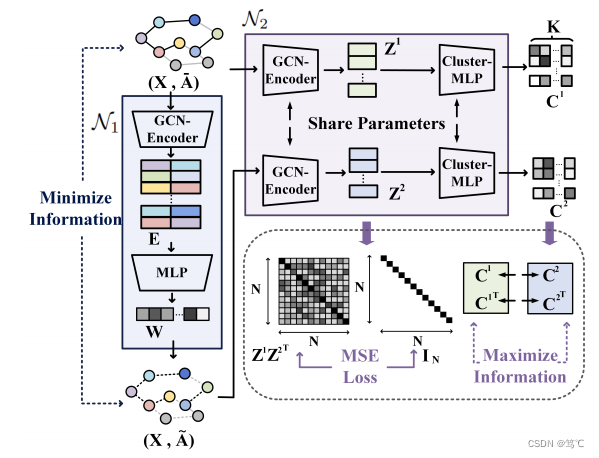
AGC-DRR由两个对抗子网络组成：N1是一个结构增强子网络，自适应地学习冗余边缘矩阵获得增强图InfoMin原则减少冗余信息在输入空间；N2聚类子网络优化InfoMax原则和LMSE损失减少潜在空间冗余。

• 最终聚类结果由C1和C2的平均值得到。

4. 方法介绍

双冗余减少（AGCDRR）的属性图聚类算法：将图的结构增强和样本聚类统一为一个通用的最小-最大优化框架，以减少输入和潜在特征空间中的信息冗余。如上图所示，AGC-DRR主要由两个组件组成，即结构增强子网络（N1）和聚类子网络（N2）。

• 接下来，将首先介绍基本符号和准备工作，然后分别详细介绍N1和N2。

4.1 基本符号

4.2 准备工作

• 图编码器：如上图所示，GCN-编码器是一个三层图卷积网络（GCN），它聚合一阶的邻居信息，更新中心节点的嵌入以进行表示学习，其表述如下：
  

• 图对比学习：与基于自动编码器的方法（通过重构图结构来学习节点表示）不同，图对比学习（GCL）旨在最大化正样本对之间的一致性，最小化负样本对之间的一致性。

  为此，互信息最大化（InfoMax）是一种常用的估计样本对之间一致性的方法。图的对比学习目标一般可以表述为：
  

4.3 聚类子网络

现有的基于GCL的聚类方法大多通过保持不同视图的潜在特征空间的一致性，来学习节点表示；然后利用经典的聚类算法（例如，K-means ），在学习到的表示形式上获得聚类结果。

• 在这种情况下，表示学习和节点聚类的优化过程是断开的，从而导致了聚类性能的次优。

4.3.1 单步聚类子网络

为了解决这个问题，作者开发了一个单步聚类子网络，它可以直接预测每个样本的聚类id的概率。具体地说，

• 在获得两个视图的图嵌入后，我们通过将Z1和Z2输入一个具有softmax激活函数的1层多层感知（MLP），将其转换为k维聚类空间，其中K表示聚类的数量。上述学习过程可表述为：
  
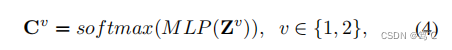
  其中$C^v\in R^{N\times K}$为第v个视图中的聚类指标矩阵。为了保持双视图聚类空间的一致性，我们重新制定了等式(3)，从样本级别的角度来看：
  
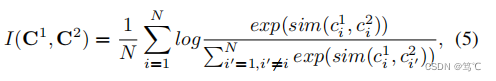
  其中，$c_i^1$和$c_i^2$分别是c1和c2中的第 i 行。为了提高聚类子网络对其他组件扰动的鲁棒性，进一步从聚类级别的角度考虑了一致性 (6)：
  
  其中，${c_j^1}^T和{c_j^2}^T$分别为c1和c2中的第 j 列。这样，通过考虑同一实例的聚类分配和两个视图中的节点分布的相似性来优化该子网络，以进一步提高聚类性能。两个观点之间的总互信息被表述为：
  

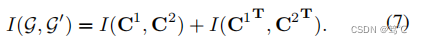
4.3.2 潜在空间冗余度的减少

尽管InfoMax原理在基于GCL的性能改进方法中起着至关重要的作用，但它可能具有使编码器在估计样本对的一致性时捕获冗余信息的风险。为了缓解这一问题，作者在潜在空间中引入了一种冗余减少策略，通过强制横视图相关矩阵近似于一个单位矩阵：

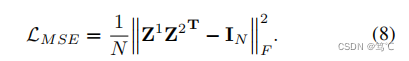
这个约束项减少了相应图中的双视图嵌入的冗余。通过这种方法，可以最小化嵌入中的冗余信息，并可以很好地保留更明显的鉴别特征。因此，它减少了学习到的表征受不相关信息的影响，从而保证了后续聚类任务的潜在空间的质量。

4.4 结构增强子网络

在现有的基于GCL的方法中，边缘扰动是网络学习前常用的图增强方法，而增广图通常被视为固定模式中的真实信息。

• 由于增广图来自于原始图，因此它将包含一些不正确的或冗余的连接。如果在网络学习过程中不消除这些噪声结构，学习到的聚类空间将在最终步骤中继承它。

为了解决这一问题，作者设计了一个结构增广子网来学习一个面向聚类的结构图，它将自适应地学习一个冗余的掉边矩阵，以确保比较样本对的多样性。

4.4.1 边权重学习

如图2所示，在N1中存在一个额外的GCN编码器，它与N2中具有相同的架构。同样，该图编码器接受归一化的相邻矩阵$\bar{A}$和节点属性矩阵X作为输入，输出嵌入$Z\in R^{N\times d^{\prime }}$的图。利用学习图嵌入Z生成边嵌入 E = { E 1 ， E 2 ， … ， E M } ∈ R M × 2 d ′ E =\{E_1，E_2，…，E_M\}∈R^{M×2d'} E={E1​，E2​，…，EM​}∈RM×2d′，其中$E_M=C（zi，zj）$，$C（\cdot ，\cdot ）$是一个拼接操作，$z_i$和$z_j$是中心节点$v_i$和邻居节点$v_j$的嵌入。然后将得到的边缘嵌入E馈入具有s型激活函数的1层MLP中，得到边向权向量$W=[w_1，w_2，\dots ，w_M]T\in R^{M\times 1}$作为等式 (9)：

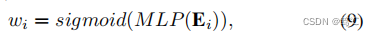
其中，$w_i$表示对应的原始边$e_i$在增广图中被保留的概率。因此，$1-w_i$表示边下降概率。

然后，我们将权值向量$W\in R^{M\times 1}$转换为一个面向边的权值矩阵$W^{\prime }\in R^{N\times N}$，生成结构增广图$G^{\prime }$。具体地说，如果节点$v_i$和节点$v_j$通过原始图中的边$e_m$连接，我们将$W_i^{\prime }j$设置为$w_m$，否则$W_i^{\prime }j$设置为零值。增广相邻矩阵$\tilde{A}$的构造公式如下：

其中⊙是阿达玛乘积（点乘），即${\tilde{A}}_{ij}=W_{ij}^{\prime }\times {\bar{A}}_{ij}$。

因此，最终的增广图$G^{\prime }$由增广相邻矩阵${\tilde{A}}_{ij}$和节点属性矩阵$X$组成。

通过最小化公式(7)，使结构增广子网能够减少输入空间中的冗余信息，以确保所比较的样本对的多样性。这样，将图结构和聚类的学习过程统一成一个共同的对抗性优化框架，使两个子网络相互受益，减轻信息冗余的风险，从而实现更好的聚类。

4.4.2 正则化项

为了尽可能多地转换冗余信息，我们在等式中引入了一个正则化项$\frac{1}{M}{\sum }_{i=1}^{M}wi$在公式(7)中，去控制结构信息保存和减少的比例，其中$w_i$表示第 $i$ 条边被保留的概率。

综上所述，${\mathcal{N}}_1$和${\mathcal{N}}_2$的目标函数可以分别表示为等式（11）和等式（12）：


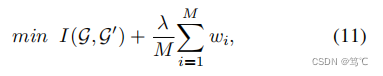
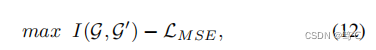
其中，λ是一个预先防御的超参数。

4.5 整体、算法流程

在如下算法中给出了AGC-DRR的训练过程。

5. 实验

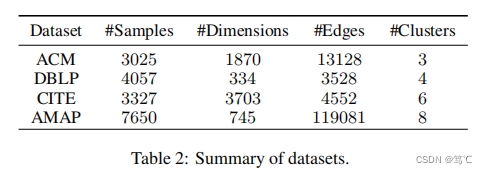
5.1 数据集

5.2 实验设置

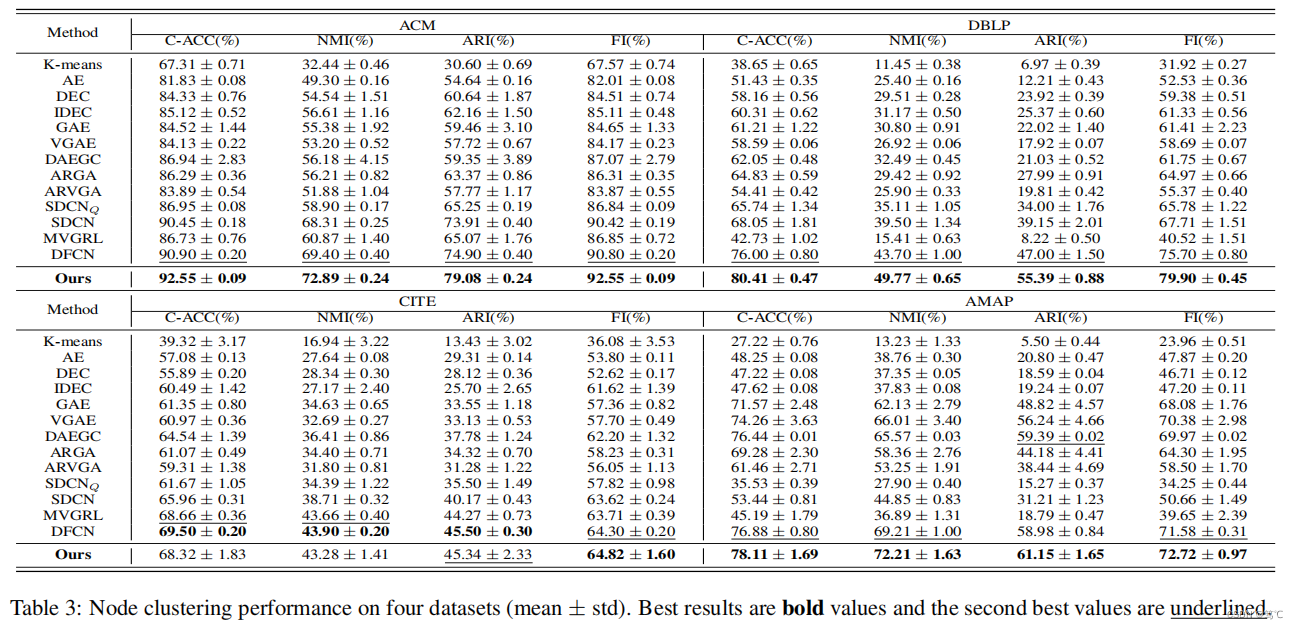
5.3 实验结果

6. 总结

论文设计了一种新的具有双冗余减少的属性图聚类（AGC-DRR），它可以减少输入特征空间和潜在特征空间中的冗余信息。

• 模型将结构增广图和聚类的学习过程结合成一个共同的最小-最大优化框架。
• 通过这种方式，学习网络对扰动具有鲁棒性，同时对类间样本具有一定的区别性。
• 所提出的AGC-DRR已经在四个基准数据集上进行了评估。
• 大量的实验结果证明了我们提出的方法优于最先进的同类方法。