一、参考资料

01背包问题 二维

https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html

视频讲解：https://www.bilibili.com/video/BV1cg411g7Y6

01背包问题 一维

https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-2.html

视频讲解：https://www.bilibili.com/video/BV1BU4y177kY

分割等和子集

本题是 01背包的应用类题目

https://programmercarl.com/0416.%E5%88%86%E5%89%B2%E7%AD%89%E5%92%8C%E5%AD%90%E9%9B%86.html

视频讲解：https://www.bilibili.com/video/BV1rt4y1N7jE

二、动态规划：01背包理论基础

背包问题：

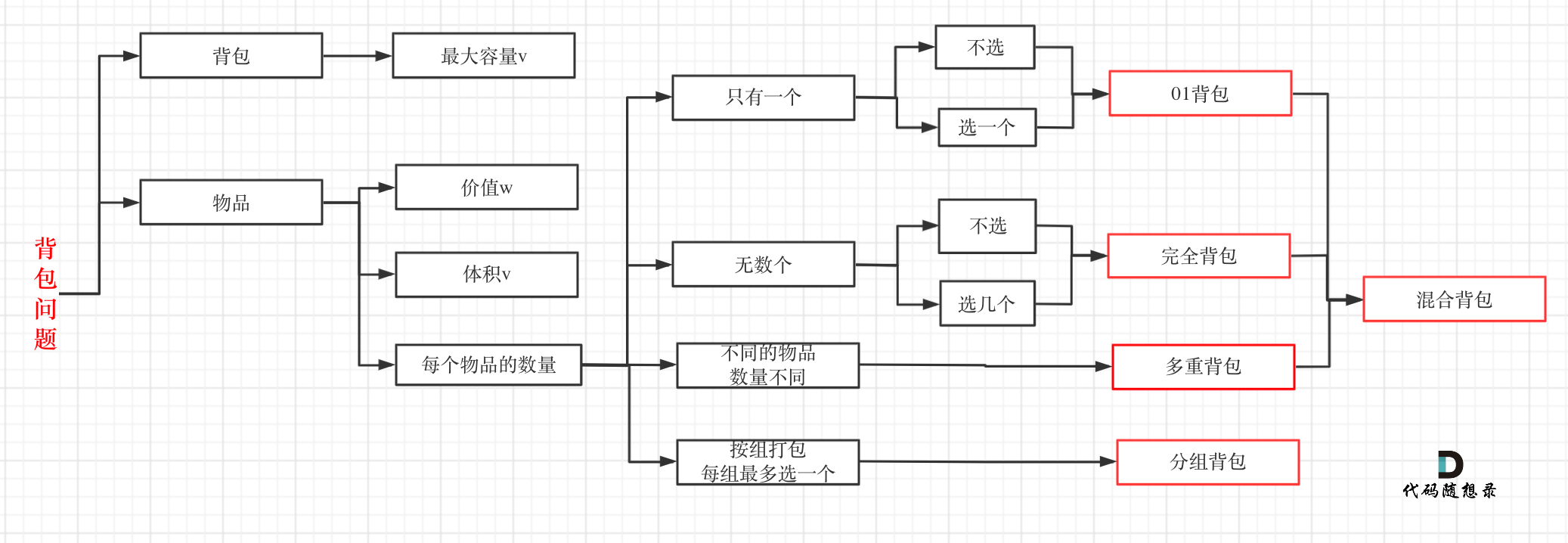
01背包-二维数组 完整C++测试代码！

void test_2_wei_bag_problem1() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagweight = 4;

    // 二维数组
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));

    // 初始化
    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    // weight数组的大小 就是物品个数
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

        }
    }

    cout << dp[weight.size() - 1][bagweight] << endl;
}

int main() {
    test_2_wei_bag_problem1();
}

Tip1：关于二维遍历的顺序，先遍历背包重量还是先遍历物品都可以，影响的是一个是先生成行再生成下一行的某一个位置的值，另一个是先生成列再生成下一列某一个位置的值。

Tip2：初始化需要注意！背包重量为0所对应的行或者列应该全部初始化为0，编号为0的物品所对应的行或列的初始化需要根据当前背包所能承受的最大重量，与当前物品的重量相比，能放下就初始化为当前物品的value。

Tip3：双层for循环，内层是正序或倒序遍历均可以，这是因为二维数组的行和列的数值是相互独立不受影响的。以物品为行，重量为列举例，下一行装物品的dp[i][j]与dp[i-1][j]是完全独立的值，每一个新的行i都会根据历史信息更新，因此不受遍历顺序的影响。

01背包-一维数组 完整C++测试代码！（滚动数组）

void test_1_wei_bag_problem() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    // 初始化
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}

int main() {
    test_1_wei_bag_problem();
}

Tip：特别注意！！此时的内层循环一定要倒序遍历，这是为了防止重复拿物品。因为状态压缩后，当前行的数组是动态变化的，某一个位置dp[j]的产生或受到新旧数据的共同影响。因此，采用倒序遍历的方式，保证物品只拿一次，满足01背包的基本需求。

三、LeetCode416. 分割等和子集

https://leetcode.cn/problems/partition-equal-subset-sum/description/

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：
输入：nums = [1,5,11,5] 输出：true 解释：数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2：
输入：nums = [1,2,3,5] 输出：false 解释：数组不能分割成两个元素和相等的子集。
提示：
1 <= nums.length <= 200
1 <= nums[i] <= 100

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        // 对数组来说，重量和价值是一样
        int sum = 0;

        // dp[i]中的i表示背包内总和
        // 题目中说：每个数组汇总的元素不会超过100，数组的大小不会超过200
        // 总和不会大于20000，背包最大只需要其中一半，所以10001大小就可以了
        vector<int> dp(10001, 0); 
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        // 也可以使用库函数一步求和
        // int sum = accumulate(nums.begin(), nums.end(), 0);
        if (sum % 2 == 1) return false;
        int target = sum / 2;

        // 开始01背包
        for (int i = 0; i < nums.size(); i++) {
            for (int j = target; j >= nums[i]; j--) {
                // 每一个元素一定是不可重复放入，所以从大到小遍历
                dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
            }
        }
        // 集合中的元素正好可以凑成总和target
        if (dp[target] == target) return true;
        return false;
    }
};

补题哇~继续Day41 √