144. 二叉树的前序遍历
难度简单
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
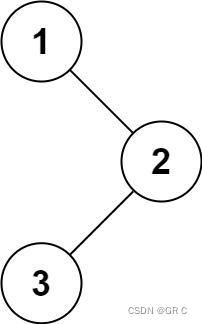
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = [ ]
输出:[ ]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
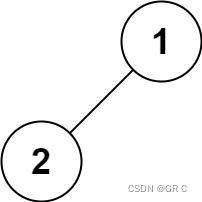
输入:root = [1,2]
输出:[1,2]
示例 5:
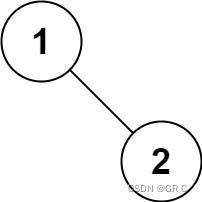
输入:root = [1,null,2]
输出:[1,2]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
进阶:递归算法很简单,你可以通过迭代算法完成吗?
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* preorderTraversal(struct TreeNode* root, int* returnSize){
}解析代码:
ps(迭代算法我们要学了C++之后的高阶数据结构再实现)
int TreeSize(struct TreeNode* root)
{
if(root==NULL)
{
return 0;
}
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
void _preorderTraversal(struct TreeNode* root,int* array,int* pi) // (函数前面的_代表这个函数的子函数)
{
if(root==NULL)
{
return;
}
array[(*pi)++] = root->val;
_preorderTraversal(root->left,array,pi);
_preorderTraversal(root->right,array,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int size = TreeSize(root);
int* array=(int*)malloc(sizeof(int)*size);
int i = 0;
_preorderTraversal(root,array,&i);
*returnSize=size;
return array;
}(写完这题可以去写写二叉树的中序遍历和后序遍历,都是一样的)链接:
94. 二叉树的中序遍历
965. 单值二叉树
难度简单
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
示例 1:
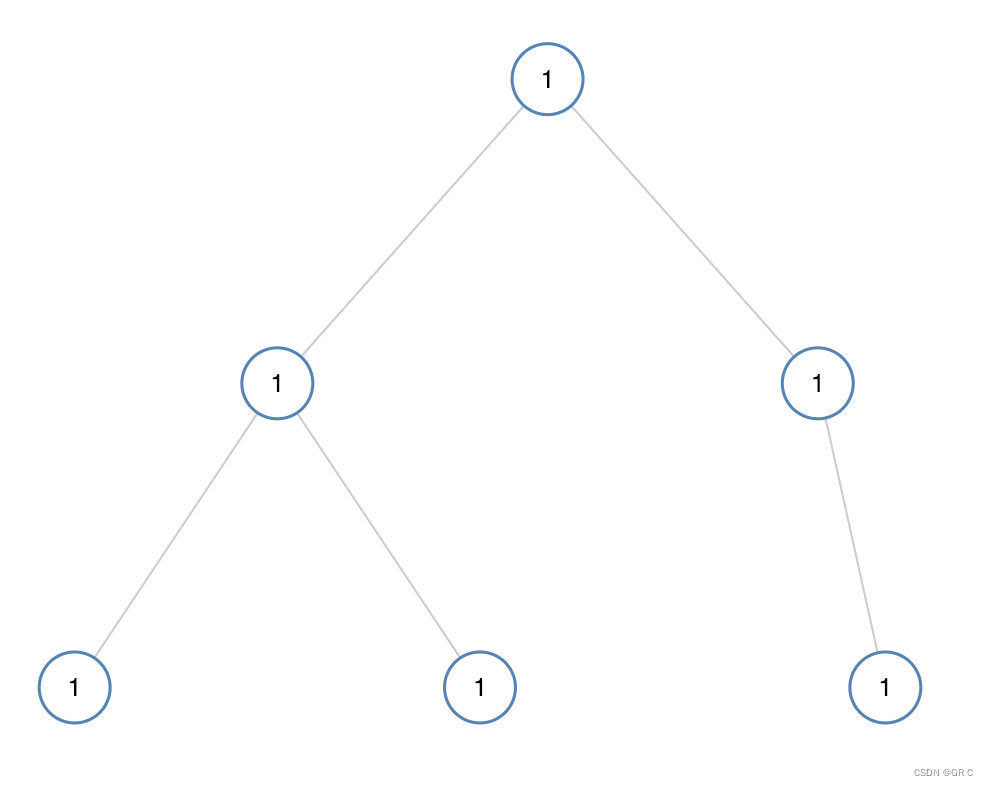
输入:[1,1,1,1,1,null,1]
输出:true
示例 2:
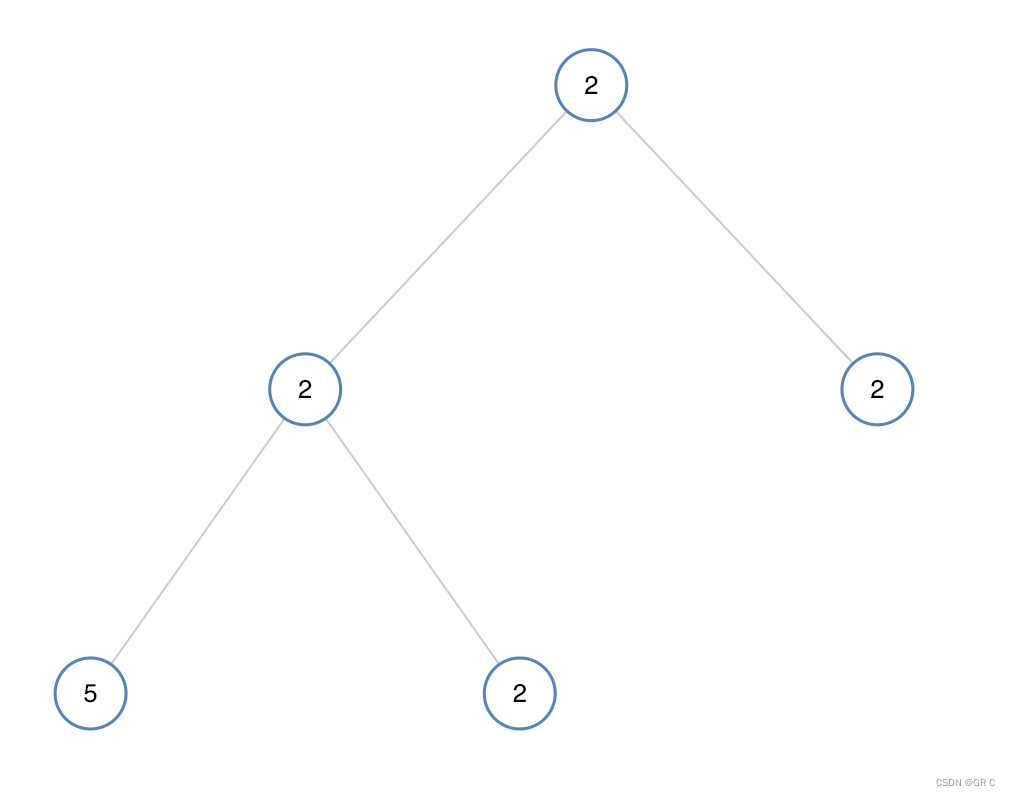
输入:[2,2,2,5,2]
输出:false
提示:
给定树的节点数范围是 [1, 100]。
每个节点的值都是整数,范围为 [0, 99] 。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isUnivalTree(struct TreeNode* root){
}解析代码:
bool isUnivalTree(struct TreeNode* root) {
if (root == NULL)
{
return true;
}
if (root->left && root->val != root->left->val)
{
return false;
}
if (root->right && root->val != root->right->val)
{
return false;
}
return isUnivalTree(root->left) && isUnivalTree(root->right);
}104. 二叉树的最大深度
难度简单
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int maxDepth(struct TreeNode* root){
}解析代码:
/*int maxDepth(struct TreeNode* root) {
if (root == NULL)
{
return 0;
}
return maxDepth(root->left) > maxDepth(root->right)
? maxDepth(root->left) + 1 : maxDepth(root->right) + 1;
}*/ //这样写会有重复的递归计算, 优化:
int maxDepth(struct TreeNode* root) {
if (root == NULL)
{
return 0;
}
int leftDepth = maxDepth(root->left);
int rightDepth = maxDepth(root->right);
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}226. 翻转二叉树
难度简单
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
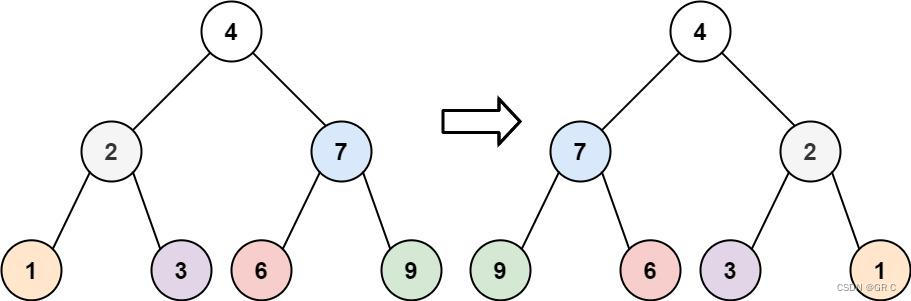
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
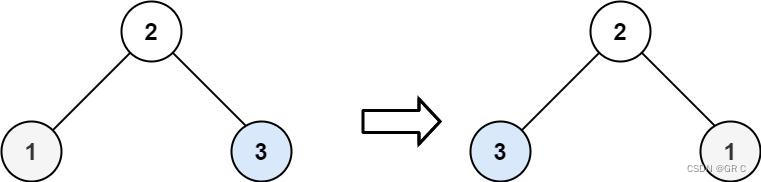
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
struct TreeNode* invertTree(struct TreeNode* root){
}解析代码(法一):
struct TreeNode* invertTree(struct TreeNode* root) {
if (root == NULL)
{
return NULL;
}
struct TreeNode* tmp = root->left;
root->left = root->right;
root->right = tmp;
invertTree(root->left);
invertTree(root->right);
return root;
}解析代码(法二):
struct TreeNode* invertTree(struct TreeNode* root) {
if (root == NULL)
{
return NULL;
}
struct TreeNode* rightTmp = root->right;
root->right = invertTree(root->left);
root->left = invertTree(rightTmp);
return root;
}100. 相同的树
难度简单
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
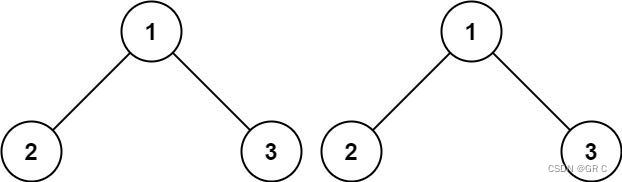
输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:

输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
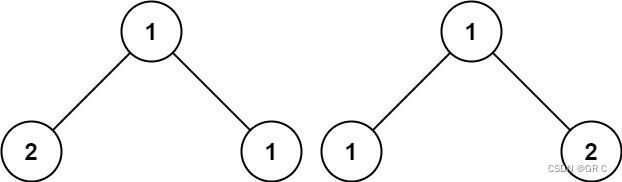
输入:p = [1,2,1], q = [1,1,2]
输出:false
提示:
两棵树上的节点数目都在范围 [0, 100] 内
-10^4 <= Node.val <= 10*4
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
}解析代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
if (p == NULL && q == NULL)
{
return true;
}
if (p == NULL || q == NULL)//其中一个为空,另一个不为空
{
return false;
}
if (p->val != q->val)
{
return false;
}
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}572. 另一棵树的子树
难度简单
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:

输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
示例 2:

输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出:false
提示:
root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-10^4 <= root.val <= 10^4
-10^4 <= subRoot.val <= 10^4
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
}解析代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if (p == NULL && q == NULL)
{
return true;
}
if (p == NULL || q == NULL)//其中一个为空,另一个不为空
{
return false;
}
if (p->val != q->val)
{
return false;
}
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
if (root == NULL)
{
return false;
}
if (isSameTree(root, subRoot))
{
return true;
}
//不一样就递归遍历这棵树
return isSubtree(root->left, subRoot)
|| isSubtree(root->right, subRoot);
//只要有一个root返回true就行
}