LeetCode 2373. 矩阵中的局部最大值

难度：$easy$

---

题目描述

给你一个大小为 $nxn$ 的整数矩阵 $grid$ 。

生成一个大小为 $(n-2)x(n-2)$ 的整数矩阵 $maxLocal$ ，并满足：

• $maxLocal[i][j]$ 等于 $grid$ 中以 $i+1$ 行和 $j+1$ 列为中心的 $3x3$ 矩阵中的 最大值 。

换句话说，我们希望找出 $grid$ 中每个 $3x3$ 矩阵中的最大值。

返回生成的矩阵。

示例 1：

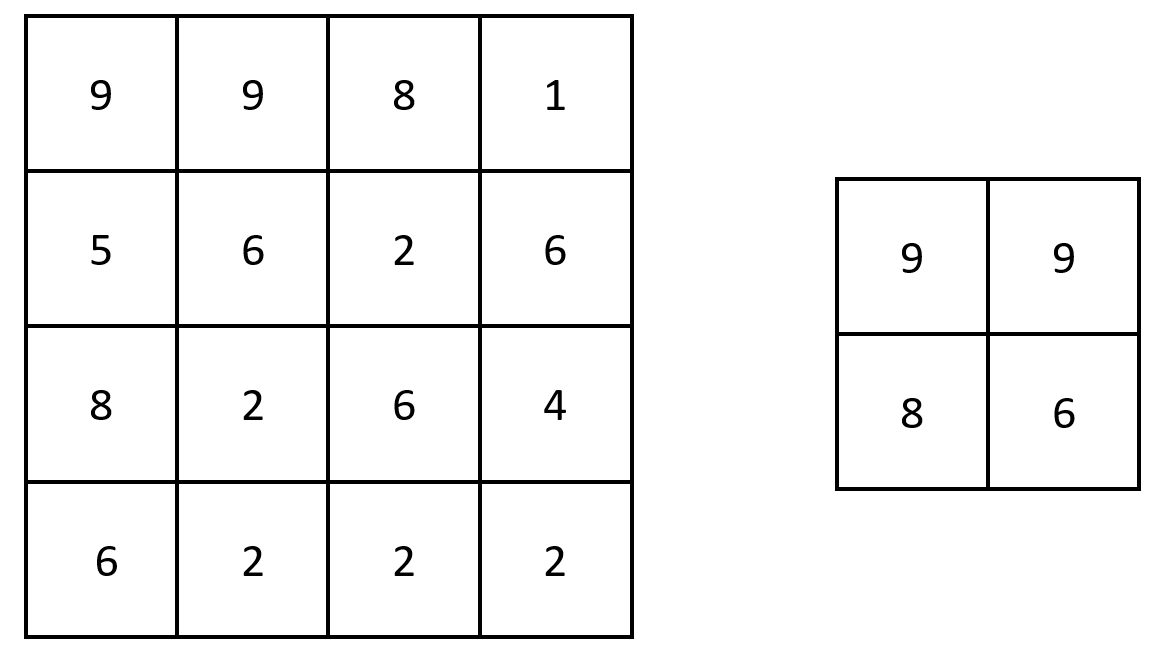
输入：grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出：[[9,9],[8,6]]
解释：原矩阵和生成的矩阵如上图所示。
注意，生成的矩阵中，每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。

示例 2：

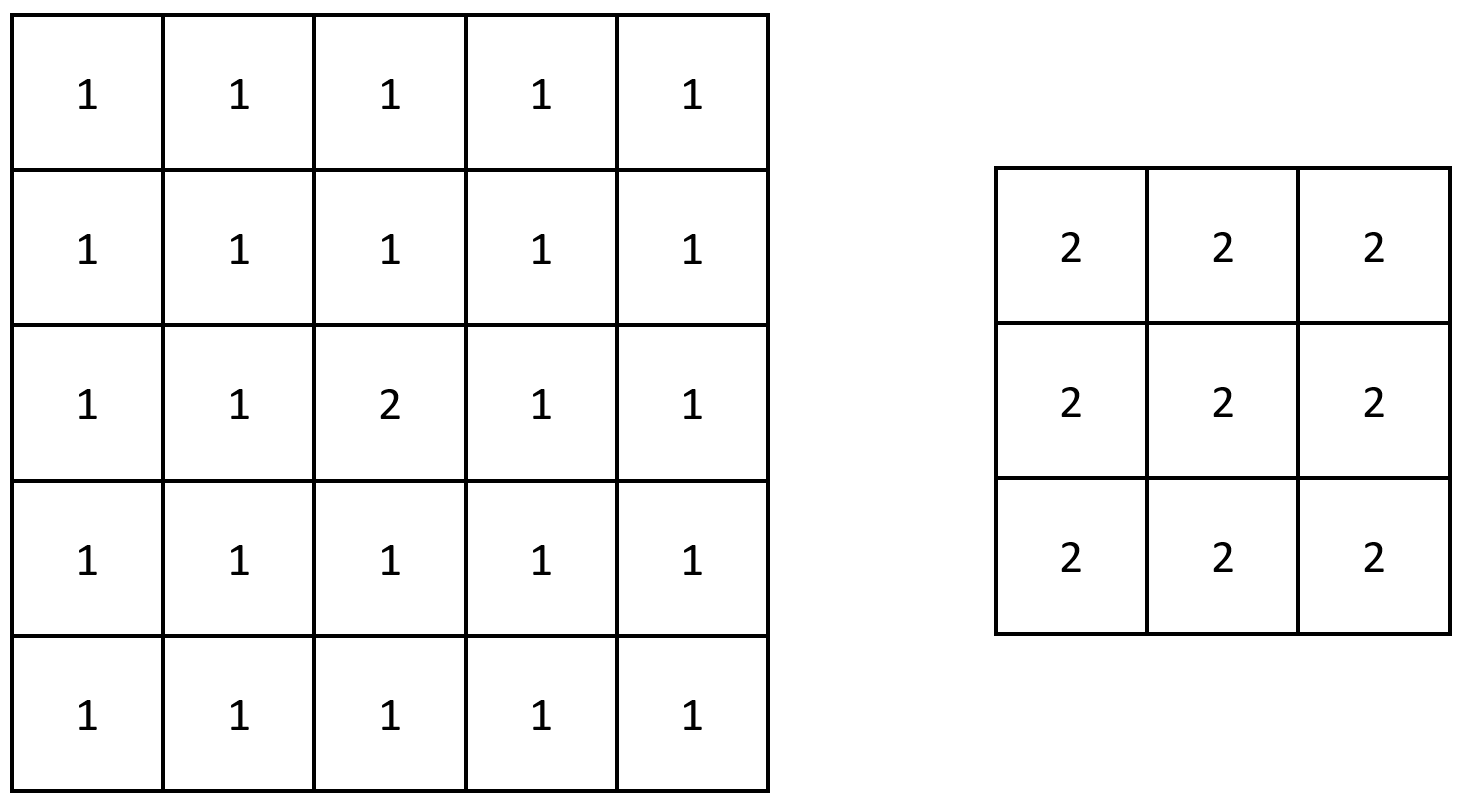
输入：grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出：[[2,2,2],[2,2,2],[2,2,2]]
解释：注意，2 包含在 grid 中每个 3 x 3 的矩阵中。

提示：

• $n==grid.length==grid[i].length$
• $3<=n<=100$
• $1<=grid[i][j]<=100$

---

算法

(遍历)

设 grid 的大小为 n×n，那么我们申请一个大小为 (n−2)×(n−2) 的矩阵 res 用来存放答案。我们遍历 grid 中每个 3×3 子矩阵的左上角，然后统计当前子矩阵的最大值放入 res 中。

具体做法是，我们顺序遍历 i (0≤i<n−2)，再顺序遍历 j (0≤j<n−2)，接着遍历求解 {grid(x,y) ∣ i≤x<i+3,j≤y<j+3} 的最大值放入
res[i][j] 中。

复杂度分析

• 时间复杂度：$O(n^2)$，其中 $n$ 是 grid 的行数。

• 空间复杂度 : $O(1)$

C++ 代码

class Solution {
public:
    
    vector<vector<int>> largestLocal(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<vector<int>> res(n - 2, vector<int>(n - 2, 0));

        for (int i = 0; i < n - 2; i ++) {
            for (int j = 0; j < n - 2; j ++) {
                for (int x = i; x < i + 3; x ++) {
                    for (int y = j; y < j + 3; y ++) {
                        res[i][j] = max(res[i][j], grid[x][y]);
                    }
                }
            }
        }

        return res;

    }
};

---