1 二叉树的定义及主要特性

1.1 二叉树的定义

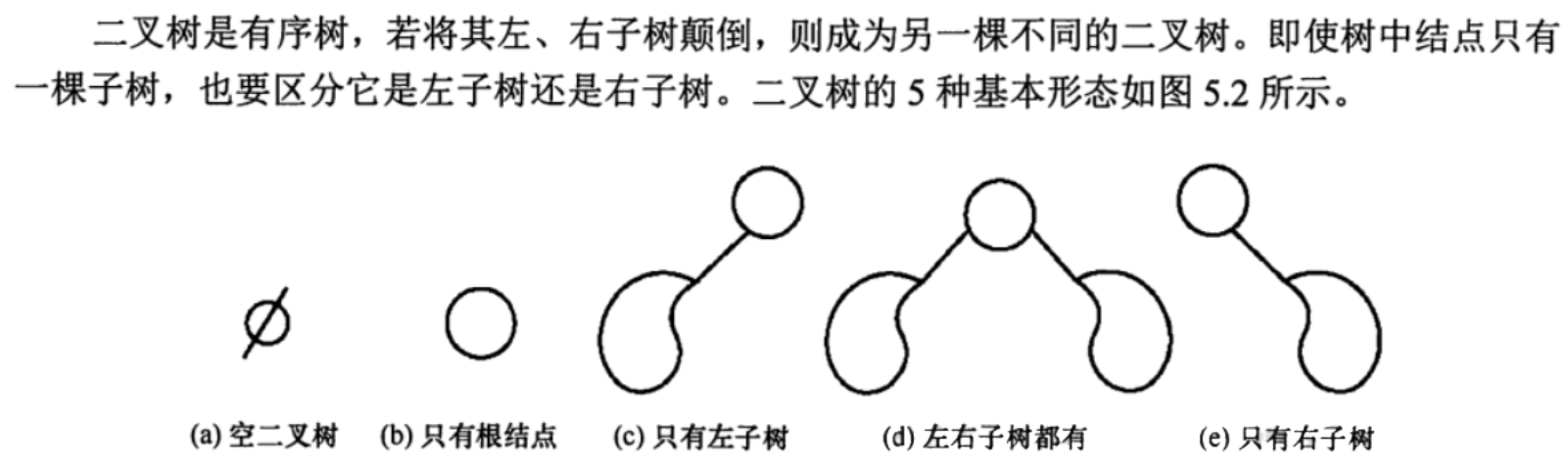
1.2 特殊二叉树

1.2.1 满二叉树

1.2.2 完全二叉树

其实这些结论不难理解，只要记住完全二叉树的基本性质，这些结论就可以很快理解。

1.2.3 二叉排序树

1.2.4 平衡二叉树

树的深度：树中结点的最大层数

1.3 二叉树的性质

1.3.1 非空二叉树上的叶结点数

1.3.2 非空二叉树第k层结点数

等比数列求和公式：
$$Sn=a_1\frac{1-q^n}{1-q}$$
其中q是公比，a1是首项。

等比数列第n项：
$$a_n=a_i{q}^{n-1}$$

1.3.3 高度为h的二叉树至多结点数

1.3.4 完全二叉树结点与双亲的关系

1.3.5 n个结点完全二叉树的高度

2 二叉树的存储结构

2.1 顺序存储结构

2.2 链式存储结构

二叉树实现链式存储参考代码：

#include <stdio.h>
#include <stdlib.h>

// 二叉树结点
typedef struct TreeNode {
    int data;
    struct TreeNode *left;
    struct TreeNode *right;
} TreeNode;

// 创建二叉树结点
TreeNode* create_node(int data) {
    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 插入结点到二叉树中
void insert_node(TreeNode** root, int data) {
    if (*root == NULL) {
        *root = create_node(data);
    } else if (data < (*root)->data) {
        insert_node(&((*root)->left), data);
    } else if (data > (*root)->data) {
        insert_node(&((*root)->right), data);
    }
}

// 中序遍历二叉树
void inorder_traversal(TreeNode* root) {
    if (root != NULL) {
        inorder_traversal(root->left);
        printf("%d ", root->data);
        inorder_traversal(root->right);
    }
}

int main() {
    // 创建二叉树
    TreeNode* root = NULL;
    insert_node(&root, 5);
    insert_node(&root, 3);
    insert_node(&root, 7);
    insert_node(&root, 2);
    insert_node(&root, 4);
    insert_node(&root, 6);
    insert_node(&root, 8);

    // 输出二叉树
    printf("Inorder traversal of binary tree: ");
    inorder_traversal(root);
    printf("\n");

    return 0;
}

附赠一张壁纸(^ ^)/~