pytorch-把线性回归实现一下。原理到实现，python到pytorch

线性回归
- 线性回归输出是一个连续值，因此适用于回归问题。回归问题在实际中很常见，如预测房屋价格、气温、销售额等连续值的问题。
- 与回归问题不同，分类问题中模型的最终输出是一个离散值。所说的图像分类、垃圾邮件识别、疾病检测等输出为离散值的问题都属于分类问题的范畴。softmax回归则适用于分类问题。
线性回归分析（Linear Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。本质上说，这种变量间依赖关系就是一种线性相关性，线性相关性是线性回归模型的理论基础,线性回归分析（Linear Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。本质上说，这种变量间依赖关系就是一种线性相关性，线性相关性是线性回归模型的理论基础。
以一个简单的房屋价格预测作为例子来解释线性回归的基本要素。这个应用的目标是预测一栋房子的售出价格（元）。我们知道这个价格取决于很多因素，如房屋状况、地段、市场行情等。为了简单起见，这里我们假设价格只取决于房屋状况的两个因素，即面积（平方米）和房龄（年）。接下来我们希望探索价格与这两个因素的具体关系。
- 模型定义
  - 设房屋的面积为 $x_1$ ，房龄为 $x_2$ ，售出价格为 $y$ 。需要建立基于输入 $x_1$ 和 $x_2$ 来计算输出 $y$ 的表达式，也就是模型（model）。顾名思义，线性回归假设输出与各个输入之间是线性关系： $\hat{y} = x_1 w_1 + x_2 w_2 + b$ 其中 $w_1$ 和 $w_2$ 是权重（weight）， $b$ 是偏差（bias），且均为标量。它们是线性回归模型的参数（parameter）。模型输出 $\hat{y}$ 是线性回归对真实价格 $y$ 的预测或估计。通常允许它们之间有一定误差。
- 模型训练
  - 训练数据
    - 通常收集一系列的真实数据，例如多栋房屋的真实售出价格和它们对应的面积和房龄。我们希望在这个数据上面寻找模型参数来使模型的预测价格与真实价格的误差最小。在机器学习术语里，该数据集被称为训练数据集（training data set）或训练集（training set），一栋房屋被称为一个样本（sample），其真实售出价格叫作标签（label），用来预测标签的两个因素叫作特征（feature）。特征用来表征样本的特点。
    - 假设我们采集的样本数为 n，索引为 i 的样本的特征为 $x_1^{(i)}$ 和 $x_2^{(i)}$ ，标签为 $y^{(i)}$ 。对于索引为 i 的房屋，线性回归模型的房屋价格预测表达式为 $\hat{y}^{(i)} = x_1^{(i)} w_1 + x_2^{(i)} w_2 + b$
  - 损失函数
    - 在模型训练中，我们需要衡量价格预测值与真实值之间的误差。通常我们会选取一个非负数作为误差，且数值越小表示误差越小。一个常用的选择是平方函数。它在评估索引为 i 的样本误差的表达式为 $\ell^{(i)}(w_1, w_2, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2$ 其中常数 $\frac 1 2$ 使对平方项求导后的常数系数为1，这样在形式上稍微简单一些。
    - 显然，误差越小表示预测价格与真实价格越相近，且当二者相等时误差为0。给定训练数据集，这个误差只与模型参数相关，因此我们将它记为以模型参数为参数的函数。在机器学习里，将衡量误差的函数称为损失函数（loss function）。这里使用的平方误差函数也称为平方损失（square loss）。
    - 通常，用训练数据集中所有样本误差的平均来衡量模型预测的质量，即
      - $\ell(w_1, w_2, b) =\frac{1}{n} \sum_{i=1}^n \ell^{(i)}(w_1, w_2, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2$
    - 在模型训练中，我们希望找出一组模型参数，记为 $w_1^*$ , $w_2^*$ , $b^*$ ，来使训练样本平均损失最小：
      - $w_1^*, w_2^*, b^* = \underset{w_1, w_2, b}{\arg\min} \ell(w_1, w_2, b)$
  - 优化算法
    - 当模型和损失函数形式较为简单时，上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解（analytical solution）。本节使用的线性回归和平方误差刚好属于这个范畴。然而，大多数深度学习模型并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解（numerical solution）。
    - 在求数值解的优化算法中，小批量随机梯度下降（mini-batch stochastic gradient descent）在深度学习中被广泛使用。它的算法很简单：先选取一组模型参数的初始值，如随机选取；接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量（mini-batch） $\mathcal{B}$ ，然后求小批量中数据样本的平均损失有关模型参数的导数（梯度），最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。
    - 在训练线性回归模型的过程中，模型的每个参数将作如下迭代：
      - $\begin{aligned} w_1 &\leftarrow w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial w_1} = w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ w_2 &\leftarrow w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial w_2} = w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial \ell^{(i)}(w_1, w_2, b) }{\partial b} = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned}$
    - 在上式中， $|\mathcal{B}|$ 代表每个小批量中的样本个数（批量大小，batch size）， $\eta$ 称作学习率（learning rate）并取正数。需要强调的是，这里的批量大小和学习率的值是人为设定的，并不是通过模型训练学出的，因此叫作超参数（hyperparameter）。通常所说的“调参”指的正是调节超参数，例如通过反复试错来找到超参数合适的值。在少数情况下，超参数也可以通过模型训练学出。
- 模型预测
  - 模型训练完成后，将模型参数 $w_1, w_2, b$ 在优化算法停止时的值分别记作 $\hat{w}_1, \hat{w}_2, \hat{b}$ 。注意，这里得到的并不一定是最小化损失函数的最优解 $w_1^*, w_2^*, b^*$ ，而是对最优解的一个近似。然后，就可以使用学出的线性回归模型 $x_1 \hat{w}_1 + x_2 \hat{w}_2 + \hat{b}$ 来估算训练数据集以外任意一栋面积（平方米）为 $x_1$ 、房龄（年）为 $x_2$ 的房屋的价格了。这里的估算也叫作模型预测、模型推断或模型测试。
线性回归的从零开始实现
- 首先，导入本节中实验所需的包或模块，其中的matplotlib包可用于作图，且设置成嵌入显示。
- ```
%matplotlib inlineag-1-1gqbc4tp7
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
```
- 生成数据集：构造一个简单的人工训练数据集，它可以使我们能够直观比较学到的参数和真实的模型参数的区别。设训练数据集样本数为1000，输入个数（特征数）为2。给定随机生成的批量样本特征 $\boldsymbol{X} \in \mathbb{R}^{1000 \times 2}$ ，使用线性回归模型真实权重 $\boldsymbol{w} = [2, -3.4]^\top$ 和偏差 $b = 4.2$ ，以及一个随机噪声项 $\epsilon$ 来生成标签 $\boldsymbol{y} = \boldsymbol{X}\boldsymbol{w} + b + \epsilon$ 其中噪声项 $\epsilon$ 服从均值为0、标准差为0.01的正态分布。噪声代表了数据集中无意义的干扰。
- ```
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.randn(num_examples, num_inputs,dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),dtype=torch.float32)   
print(features, features.shape)
print(labels, labels.shape)
```
- ```
tensor([[ 0.6216, -0.1328],
        [-0.5391,  0.0832],
        [ 1.2280,  0.8949],
        ...,
        [ 0.4977,  0.0283],
        [-0.2189, -0.4873],
        [ 1.5165,  0.0500]]) torch.Size([1000, 2])
tensor([  5.8867,   2.8264,   3.6247,   8.8301,   6.4663,  -2.2984,   0.0459,...]) torch.Size([1000])
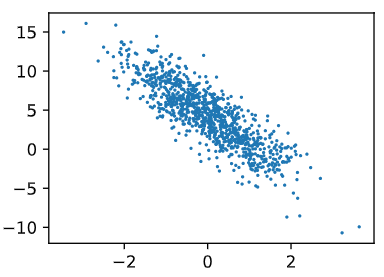
```
- 通过生成第二个特征features[:, 1]和标签 labels 的散点图，可以更直观地观察两者间的线性关系。
- ```
def use_svg_display():
    # 用矢量图显示
    display.display_svg()
def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    # 设置图的尺寸
    plt.rcParams['figure.figsize'] = figsize
set_figsize()
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1);
```
- 读取数据:在训练模型的时候，我们需要遍历数据集并不断读取小批量数据样本。这里我们定义一个函数：它每次返回batch_size（批量大小）个随机样本的特征和标签。读取第一个小批量数据样本并打印。每个批量的特征形状为(10, 2)，分别对应批量大小和输入个数；标签形状为批量大小。
  - ```
  def data_iter(batch_size, features, labels):
      num_examples = len(features)
      indices = list(range(num_examples))   # 生成下标列表
      random.shuffle(indices)  # 打乱下标列表，样本的读取顺序是随机的
      for i in range(0, num_examples, batch_size):
          j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batch
          yield  features.index_select(0, j), labels.index_select(0, j)
  batch_size = 10
  index = 0
  for X, y in data_iter(batch_size, features, labels):
      print(X, y)
      index += 1
      if index >2:
          break
```
- ```
tensor([[ 1.2572, -0.0569],
        [-1.0629,  0.5675],
        [ 0.2812,  1.1647],
        [ 1.3334, -0.3296],
        [ 0.6850, -1.2253],
        [ 0.6851,  0.4158],
        [ 0.0727,  0.9224],
        [-0.7991, -0.1419],
        [ 0.7741,  1.6103],
        [-0.2893, -0.7415]]) tensor([6.9151, 0.1457, 0.8034, 8.0023, 9.7363, 4.1549, 1.2025, 3.0689, 0.2749,
        6.1371])
tensor([[ 1.4936,  1.5380],
        [ 0.0410,  0.4386],
        [ 0.4641, -0.3789],
        [-0.5353,  0.5551],
        [-1.2910, -0.8273],
        [ 0.4035, -0.5826],
        [-0.8060, -0.5223],
        [ 0.9478,  0.6716],
        [-1.7344,  0.2920],
        [-0.5045,  1.3026]]) tensor([ 1.9619,  2.7909,  6.4143,  1.2321,  4.4248,  6.9789,  4.3647,  3.8035,
        -0.2623, -1.2338])
tensor([[-0.4643,  1.2070],
        [ 1.2244,  1.0575],
        [-0.5904, -0.8998],
        [ 0.3056, -0.4934],
        [ 0.1183,  0.1850],
        [-0.1599,  0.3071],
        [ 0.8133,  0.1455],
        [-0.8600, -0.5746],
        [ 0.9954,  1.7316],
        [-0.1285,  0.9870]]) tensor([-0.8267,  3.0593,  6.0694,  6.4741,  3.8124,  2.8426,  5.3399,  4.4488,
         0.2982,  0.5795])
```
- 初始化模型参数:将权重初始化成均值为0、标准差为0.01的正态随机数，偏差则初始化成0。之后的模型训练中，需要对这些参数求梯度来迭代参数的值，因此我们要让它们的requires_grad=True。
  - ```
  w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
  b = torch.zeros(1, dtype=torch.float32)
  w.requires_grad_(requires_grad=True)
  b.requires_grad_(requires_grad=True) 
  print(w,b)
```
- ```
tensor([[-0.0267],
        [ 0.0070]], requires_grad=True) tensor([0.], requires_grad=True)
```
- 定义模型
  - 线性回归的矢量计算表达式的实现。使用mm函数做矩阵乘法。
    - torch.mul(a, b) 是矩阵a和b对应位相乘，a和b的维度必须相等，比如a的维度是(1, 2)，b的维度是(1, 2)，返回的仍是(1, 2)的矩阵；
    - torch.mm(a, b) 是矩阵a和b矩阵相乘，比如a的维度是(1, 2)，b的维度是(2, 3)，返回的就是(1, 3)的矩阵;
    - torch.bmm() 强制规定维度和大小相同;
    - torch.matmul() 没有强制规定维度和大小，可以用利用广播机制进行不同维度的相乘操作
  - ```
  def linreg(X, w, b): 
      return torch.mm(X, w) + b
```
- 定义损失函数
  - 评价指标是针对将相同的数据，输入不同的算法模型，或者输入不同参数的同一种算法模型，而给出这个算法或者参数好坏的定量指标
    - 均方误差（SSE）：真实值-预测值然后平方之后求和平均
      - 同样的数据集的情况下，SSE越小，误差越小，模型效果越好。
      - 缺点：SSE数值大小本身没有意义，随着样本增加，SSE必然增加，也就是说，不同的数据集的情况下，SSE比较没有意义。
      - $SSE=\sum(\hat{y}-y)^2$
      - 对SSE改进，MSE：对SSE求平均。是线性回归中最常用的损失函数，线性回归过程中尽量让该损失函数最小。那么模型之间的对比也可以用它来比较
      - $MSE=\frac{1}{m}\sum(\hat{y}-y)^2$
    - 均方根误差（标准误差 RMSE）
      - MSE是用来衡量一组数自身的离散程度，而RMSE是用来衡量观测值同真值之间的偏差，它们的研究对象和研究目的不同。它的意义在于开个根号后，误差的结果就与数据是一个级别的，可以更好地来描述数据。标准误差对一组测量中的特大或特小误差反映非常敏感，所以，标准误差能够很好地反映出测量的精密度。这正是标准误差在工程测量中广泛被采用的原因。
      - 当数据集中有一个特别大的异常值，这种情况下，### 数据倾斜，RMSE会被明显拉大。所以对RMSE低估值（under-predicted）的判罚明显小于估值过高(over-predicted)的情况。
      - $RMSE=\sqrt{\frac{1}{m}\sum({\hat{y}-y})^2}$
    - 平均绝对误差（MAE）
      - 平均绝对误差是绝对误差的平均值，平均绝对误差能更好地反映预测值误差的实际情况.
      - MAE是一个线性的指标，所有个体差异在平均值上均等加权，所以它更加凸显出异常值。MSE和MAE适用于误差相对明显的时候，此时大的误差也有比较高的权重。
      - $MAE=\frac{1}{m}\sum|\hat{y}-y|$
    - R-square(决定系数)
      - 对于回归类算法而言，只探索数据预测是否准确是不足够的。除了数据本身的数值大小之外，还希望模型能够捕捉到数据的”规律“，比如数据的分布规律，单调性等等，而是否捕获了这些信息并无法使用MSE或者MAE来衡量.
      - $R^2=1-\frac{\sum(\hat{y}^i-y^i)^2}{\sum(\bar{y}-y^i)^2}$
      - 上面分子就是我们训练出的模型预测的误差和
        下面分母就是瞎猜的误差和。（通常取观测值的平均值）
        如果结果是0，就说明我们的模型跟瞎猜差不多
        如果结果是1。就说明我们模型无错误
        介于0~1之间，越接近1，回归拟合效果越好，一般认为超过0.8的模型拟合优度比较高
      - 数学理解：分母理解为原始数据的离散程度，分子为预测数据和原始数据的误差，二者相除可以消除原始数据离散程度的影响。
      - 分子分母同时除以m，那么分子就变成了我们的均方误差MSE，下面分母就变成了方差
      - $R^2=1-\frac{MSE(\hat{y}^i,y)}{Var(y)}$
      - 方差的本质是任意一个值和样本均值的差异，差异越大，这些值所带的信息越多.在R2中，分子是真实值和预测值之差的差值，也就是我们的模型没有捕获到的信息总量，分母是真实标签所带的信息量，所以两者都衡量1 - 我们的模型没有捕获到的信息量占真实标签中所带的信息量的比例，所以，两者都是越接近1越好。数据集的样本越大，R²越大，因此，不同数据集的模型结果比较会有一定的误差。
    - Adjusted R-Square (校正决定系数）
      - $R_a^2=1-\frac{(1-R^2)(n-1)}{n-p-1}$
      - n为样本数量，p为特征数量。同时消除了样本数量和特征数量的影响
  - 这里使用上文描述的平方损失来定义线性回归的损失函数。在实现中，我们需要把真实值y变形成预测值y_hat的形状。以下函数返回的结果也将和y_hat的形状相同。
  - ```
  def squared_loss(y_hat, y):  
      # 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
      return (y_hat - y.view(y_hat.size())) ** 2 / 2
```
- 定义优化算法
  - 以下的sgd函数实现了上文中介绍的小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。这里自动求梯度模块计算得来的梯度是一个批量样本的梯度和。将它除以批量大小来得到平均值。
  - ```
  def sgd(params, lr, batch_size): 
      for param in params:
          param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
```
- 训练模型
  - 在训练中，将多次迭代模型参数。在每次迭代中，根据当前读取的小批量数据样本（特征X和标签y），通过调用反向函数backward计算小批量随机梯度，并调用优化算法sgd迭代模型参数。由于我们之前设批量大小batch_size为10，每个小批量的损失l的形状为(10, 1)。由于变量l并不是一个标量，所以可以调用.sum()将其求和得到一个标量，再运行l.backward()得到该变量有关模型参数的梯度。注意在每次更新完参数后不要忘了将参数的梯度清零。
  - 在一个迭代周期（epoch）中，将完整遍历一遍data_iter函数，并对训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设10和0.03。在实践中，大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越大模型可能越有效，但是训练时间可能过长。
  - ```
  lr = 0.03
  num_epochs = 10
  net = linreg
  loss = squared_loss
  for epoch in range(num_epochs):  # 训练模型一共需要num_epochs个迭代周期
      # 在每一个迭代周期中，会使用训练数据集中所有样本一次（假设样本数能够被批量大小整除）。X
      # 和y分别是小批量样本的特征和标签
      for X, y in data_iter(batch_size, features, labels):
          l = loss(net(X, w, b), y).sum()  # l是有关小批量X和y的损失
          l.backward()  # 小批量的损失对模型参数求梯度
          sgd([w, b], lr, batch_size)  # 使用小批量随机梯度下降迭代模型参数
          # 不要忘了梯度清零
          w.grad.data.zero_()
          b.grad.data.zero_()
      train_l = loss(net(features, w, b), labels)
      print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item())) 
```
- ```
epoch 1, loss 0.032868
epoch 2, loss 0.000126
epoch 3, loss 0.000046
epoch 4, loss 0.000046
epoch 5, loss 0.000046
epoch 6, loss 0.000046
epoch 7, loss 0.000046
epoch 8, loss 0.000046
epoch 9, loss 0.000046
epoch 10, loss 0.000046
```
- 训练完成后，可以比较学到的参数和用来生成训练集的真实参数。仅使用Tensor和autograd模块就可以很容易地实现一个模型。
  - ```
  print(true_w, '\n', w)
  print(true_b, '\n', b)
```
- ```
[2, -3.4] 
 tensor([[ 2.0002],
        [-3.3997]], requires_grad=True)
4.2 
 tensor([4.1999], requires_grad=True)
```

上文从python的角度梳理了流程实现了回归任务，现在用pytorch重新做一遍。

生成数据集：生成与上一节中相同分布的数据集。其中features是训练数据特征，labels是标签。

num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float) # 添加扰动噪声
print(features[:3], features.shape)
print(labels[:3], labels.shape)

tensor([[ 0.0060, -0.5646],
        [ 2.6077, -0.2698],
        [-1.2894, -1.1564]]) torch.Size([1000, 2])
tensor([ 6.1333, 10.3299,  5.5643]) torch.Size([1000])

读取数据

PyTorch提供了data包来读取数据。由于data常用作变量名，导入的data模块用Data代替。在每一次迭代中，将随机读取包含10个数据样本的小批量。

import torch.utils.data as Data
batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 随机读取小批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
iter_num = 0
for X, y in data_iter:
    print(X, y)
    iter_num += 1
    if iter_num > 2:
        break

tensor([[ 0.0067,  0.1401],
        [-1.1505,  0.1468],
        [ 1.5391,  1.0936],
        [ 0.4877, -1.5252],
        [ 0.7110, -0.7665],
        [-0.3763,  1.2381],
        [ 1.0921, -1.0217],
        [-0.6782, -0.0704],
        [ 0.7332, -0.4158],
        [ 0.7919, -0.4500]]) tensor([ 3.7506,  1.3989,  3.5617, 10.3682,  8.2230, -0.7610,  9.8584,  3.0777,
         7.0842,  7.3240])
tensor([[ 0.6080, -0.2581],
        [ 0.5077,  1.8393],
        [ 0.6369,  2.1997],
        [-0.6904, -1.0292],
        [-1.1829, -1.8127],
        [ 2.2175,  1.7429],
        [-0.7929, -0.8644],
        [-0.3622, -1.4727],
        [-2.0080,  1.4671],
        [ 0.1746,  0.5394]]) tensor([ 6.2746, -1.0449, -2.0096,  6.3014,  7.9963,  2.7291,  5.5671,  8.4808,
        -4.7977,  2.7139])
tensor([[ 0.8790, -1.4681],
        [-0.8629, -0.3203],
        [-0.3763,  0.0022],
        [-0.8903, -0.6009],
        [ 0.4797, -0.6693],
        [ 0.5890, -0.5540],
        [-0.1996,  0.9864],
        [-0.9645,  1.6157],
        [ 1.0762, -0.0679],
        [-0.4368, -0.8553]]) tensor([10.9561,  3.5650,  3.4371,  4.4402,  7.4297,  7.2489,  0.4353, -3.2319,
         6.5702,  6.2362])

定义模型

PyTorch提供了大量预定义的层，这使我们只需关注使用哪些层来构造模型。下面将介绍如何使用PyTorch更简洁地定义线性回归。
首先，导入torch.nn模块。实际上，“nn”是neural networks（神经网络）的缩写。顾名思义，该模块定义了大量神经网络的层。之前我们已经用过了autograd，而nn就是利用autograd来定义模型。nn的核心数据结构是Module，它是一个抽象概念，既可以表示神经网络中的某个层（layer），也可以表示一个包含很多层的神经网络。在实际使用中，最常见的做法是继承nn.Module，撰写自己的网络/层。一个nn.Module实例应该包含一些层以及返回输出的前向传播（forward）方法。

import torch.nn as nn
class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()
        self.linear = nn.Linear(n_feature, 1)
    # forward 定义前向传播
    def forward(self, x):
        y = self.linear(x)
        return y
net = LinearNet(num_inputs)
print(net) # 使用print可以打印出网络的结构

LinearNet(
  (linear): Linear(in_features=2, out_features=1, bias=True)
)

事实上还可以用nn.Sequential来更加方便地搭建网络，Sequential是一个有序的容器，网络层将按照在传入Sequential的顺序依次被添加到计算图中。

# 写法一
net = nn.Sequential(
    nn.Linear(num_inputs, 1)
    # 此处还可以传入其他层
    )
print(net)
print(net[0])
# 写法二
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......
print(net)
print(net[0])
# 写法三
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
          ('linear', nn.Linear(num_inputs, 1))
          # ......
        ]))
print(net)
print(net[0])

Sequential(
  (0): Linear(in_features=2, out_features=1, bias=True)
)
Linear(in_features=2, out_features=1, bias=True)
Sequential(
  (linear): Linear(in_features=2, out_features=1, bias=True)
)
Linear(in_features=2, out_features=1, bias=True)
Sequential(
  (linear): Linear(in_features=2, out_features=1, bias=True)
)
Linear(in_features=2, out_features=1, bias=True)

可以通过net.parameters()来查看模型所有的可学习参数，此函数将返回一个生成器。

for param in net.parameters():
    print(param)

Parameter containing:
tensor([[-0.4808, -0.0012]], requires_grad=True)
Parameter containing:
tensor([-0.4288], requires_grad=True)

注意：torch.nn仅支持输入一个batch的样本不支持单个样本输入，如果只有单个样本，可使用input.unsqueeze(0)来添加一维。

初始化模型参数
- 在使用net前，需要初始化模型参数，如线性回归模型中的权重和偏差。PyTorch在init模块中提供了多种参数初始化方法。这里的init是initializer的缩写形式。通过init.normal_将权重参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布。偏差会初始化为零。
- ```
from torch.nn import init
init.normal_(net[0].weight, mean=0, std=0.01)
init.constant_(net[0].bias, val=0)  # 也可以直接修改bias的data: net[0].bias.data.fill_(0)
```
- ```
Parameter containing:
tensor([[-0.0059,  0.0122]], requires_grad=True)
```
- 在实践中，权重是否合理的进行了初始化，决定着模型的很多走向，比如模型算法离最优解的距离远近或方向是否准确、是否会出现梯度爆炸或梯度消失从而导致训练无法收敛、同等效果下需要花多长时间来训练等。合理的权重初始化会让模型算法梯度更加正常且更加容易到达全局最优解。同样反过来，不合理权重初始化很容易让模型算法出现梯度问题，让模型算法陷入局部最优解导致训练失败等。
定义损失函数
- PyTorch在nn模块中提供了各种损失函数，这些损失函数可看作是一种特殊的层，PyTorch也将这些损失函数实现为nn.Module的子类。我们现在使用它提供的均方误差损失作为模型的损失函数。
- ```
loss = nn.MSELoss()
```
定义优化算法
- 同样，我们也无须自己实现小批量随机梯度下降算法。torch.optim模块提供了很多常用的优化算法比如SGD、Adam和RMSProp等。下面我们创建一个用于优化net所有参数的优化器实例，并指定学习率为0.03的小批量随机梯度下降（SGD）为优化算法。
- ```
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)
print(optimizer)
```
- ```
SGD (
Parameter Group 0
    dampening: 0
    differentiable: False
    foreach: None
    lr: 0.03
    maximize: False
    momentum: 0
    nesterov: False
    weight_decay: 0
)
```
- 还可以为不同子网络设置不同的学习率，这在finetune时经常用到。例：
- ```
optimizer =optim.SGD([
                # 如果对某个参数不指定学习率，就使用最外层的默认学习率
                {'params': net.subnet1.parameters()}, # lr=0.03
                {'params': net.subnet2.parameters(), 'lr': 0.01}
            ], lr=0.03)
```
- 有时候不想让学习率固定成一个常数，那如何调整学习率呢？主要有两种做法。一种是修改optimizer.param_groups中对应的学习率，另一种是更简单也是较为推荐的做法——新建优化器，由于optimizer十分轻量级，构建开销很小，故而可以构建新的optimizer。但是后者对于使用动量的优化器（如Adam），会丢失动量等状态信息，可能会造成损失函数的收敛出现震荡等情况。
- ```
# 调整学习率
for param_group in optimizer.param_groups:
    param_group['lr'] *= 0.1 # 学习率为之前的0.1倍
```

训练模型

训练模型时，我们通过调用optim实例的step函数来迭代模型参数。按照小批量随机梯度下降的定义，我们在step函数中指明批量大小，从而对批量中样本梯度求平均。

num_epochs = 10
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        output = net(X)
        l = loss(output, y.view(-1, 1))
        optimizer.zero_grad() # 梯度清零，等价于net.zero_grad()
        l.backward()
        optimizer.step()
    print('epoch %d, loss: %f' % (epoch, l.item()))

epoch 1, loss: 0.000135
epoch 2, loss: 0.000071
epoch 3, loss: 0.000055
epoch 4, loss: 0.000074
epoch 5, loss: 0.000086
epoch 6, loss: 0.000182
epoch 7, loss: 0.000060
epoch 8, loss: 0.000148
epoch 9, loss: 0.000115
epoch 10, loss: 0.000139

下面分别比较学到的模型参数和真实的模型参数。从net获得需要的层，并访问其权重（weight）和偏差（bias）。

dense = net[0]
print(true_w, dense.weight)
print(true_b, dense.bias)

[2, -3.4] Parameter containing:
tensor([[ 1.9990, -3.3997]], requires_grad=True)
4.2 Parameter containing:
tensor([4.2000], requires_grad=True))

使用PyTorch可以更简洁地实现模型。torch.utils.data模块提供了有关数据处理的工具，torch.nn模块定义了大量神经网络的层，torch.nn.init模块定义了各种初始化方法，torch.optim模块提供了很多常用的优化算法。
epoch 10, loss: 0.000139
```
- 下面分别比较学到的模型参数和真实的模型参数。从net获得需要的层，并访问其权重（weight）和偏差（bias）。
- ```
dense = net[0]
print(true_w, dense.weight)
print(true_b, dense.bias)
```
- ```
[2, -3.4] Parameter containing:
tensor([[ 1.9990, -3.3997]], requires_grad=True)
4.2 Parameter containing:
tensor([4.2000], requires_grad=True))
```
使用PyTorch可以更简洁地实现模型。torch.utils.data模块提供了有关数据处理的工具，torch.nn模块定义了大量神经网络的层，torch.nn.init模块定义了各种初始化方法，torch.optim模块提供了很多常用的优化算法。