1. Introduction
The stacking model is very common in Kaglle competitions. Why?
【机器学习大杀器】Stacking堆叠模型(English)
1. Introduction
2. Model 3: Stacking model
2.1 description of the algorithms:
2.2 interpretation of the estimated models:
3. Extend
3.1 code sample
3.2 the coefficient of last model
2. Model 3: Stacking model
===============================================
Include three model:
=================
- Lasso;
- Random Forest;
- Gradient Boost.
==============================================================
2.1 description of the algorithms:
When we get three models with equal robustness but different structure, which model should we choose at this time? I think this is a very difficult thing, but through the integrated learning method, we can easily synthesize these three models into a better model that absorbs the advantages of each model. Stacking is just such a strategy for merging models.
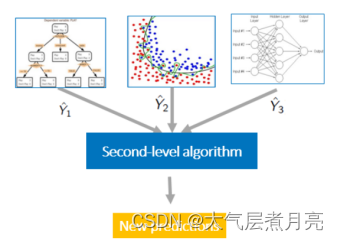
In this experiment, we just used such a stacking strategy, which greatly improved the effect of our model. In the first layer of the model, there are three stacked models: {1.Lasso, 2.Random Forest, 3.Gradient Boost}, and used {Logistics Region} as the second layer of the model.
2.2 interpretation of the estimated models:
Stacking is generally composed of two layers. Level 1: basic models with excellent performance (there can be multiple models); The second layer: take the output of the models in the first layer as the model obtained from the training set. The second layer model is also called "meta model". The key role is to integrate the results of all models in the first layer and output them. That is, the second layer model trains the output of the first layer model as a feature. The overall steps of stacking are as follows:
- The original data is divided into two parts: training set D-train and test set D-test. The training set is used to train the overall Stacking integration model, and the test set is used to test the integration model.
- This step includes training and testing:
- Training Stacking is based on cross validation. Taking the 50 fold cross validation as an example, the training set D-train is divided into five parts, trained five times, and each time an unselected part is selected as the validation set, as shown in the following figure. Wherein, Learn corresponds to Training folds, which is used to train primary learners; The Predict in the following figure corresponds to Validation fold, which is used to obtain five prediction results Predictions_Train={p1,p2,p3,p4,p5} through the primary trainer. These prediction results will be combined into a new training set, which will be used to train the secondary learner Model2.
-
Testing Five tests are also required for five times of training. After training the model once each time, the data of the test set is also tested. Finally, five prediction test set results are obtained. The average of the five prediction results is taken as the final prediction result Predictions_Test={p1,p2,p3,p4,p5} of the model of this layer. The model of the next layer will be tested on the new test set Predictions_Train.
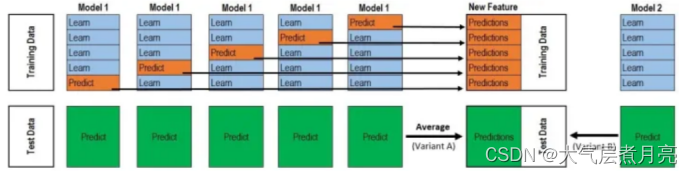
3. If there are n models stacked in the first layer, perform the operation in step 3 for each model, and finally get n Predictions_Train and Predictions_Test, put n redictions_Train as the characteristic value into the second layer model for training. After training, use the second layer model to predict the test set, and finally take the combined result of n+1 Predictions_Test as the final prediction result.
3. Extend
3.1 code sample
from sklearn.ensemble import StackingRegressor
models = [('Lasso', lo), ('Random Forest', rf), ('Gradient Boost', gb_boost)]
stack = StackingRegressor(models, final_estimator=LinearRegression(positive=True), cv=5, n_jobs=4)
stack.fit(x_train, y_train)
stack_log_pred = stack.predict(x_test)
print(stack_log_pred)
stack_pred = np.exp(stack_log_pred)
plt.barh(np.arange(len(models)), stack.final_estimator_.coef_)
plt.yticks(np.arange(len(models)), ['Linear Regression', 'Random Forest', 'Gradient Boost']);
plt.xlabel('Model coefficient')
plt.title('Figure 4. Model coefficients for our stacked model');3.2 the coefficient of last model
In order to better understand what Stacking has done, we printed the coefficient of the last layer of the Stacking model, i.e. the second layer of the Linear Regression model, after we completed the training with skleran, as shown in the figure:
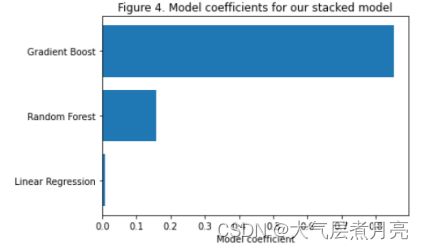
Coefficients of high and positive linear regression models coef_ It means a stronger relationship. From the above figure, we can see that the proportion of the three models we combined in Stacking is 8:2:0. It can be seen that Gradient Boost has the greatest impact on the overall prediction results of the model.